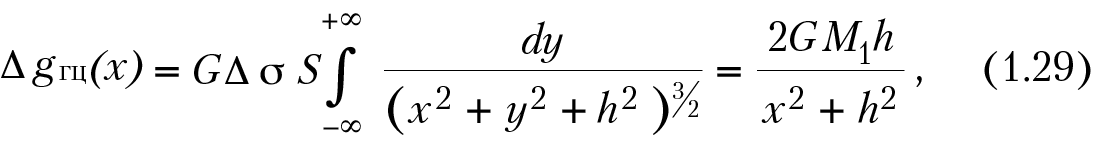Файл: Минобрнауки российской федерации министерство высшего и среднего специального образования республики узбекистан.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.11.2023
Просмотров: 54
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
С
Р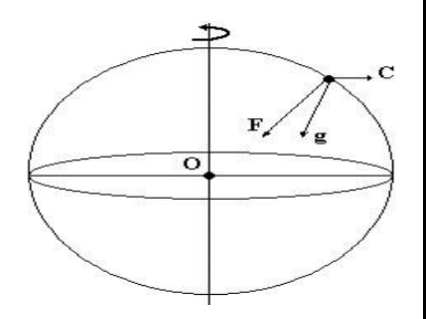
ис. 2. Сила тяжести g равна векторной сумме ньютоновской силы притяжения F и центробежной силы С.
Центробежная сила уменьшает ньютоновскую силу притяжения. На полюсах Земли, где центробежная сила отсутствует, сила тяжести g максимальна. Увеличение силы тяжести на полюсах вызвано также уменьшением полярного радиуса Земли, примерно на 21 км вследствие ее сжатия, вызванного вращением последней, и равного примерно 1/298.24, что приводит к дополнительному увеличению силы тяжести еще примерно на 1,8 Гал.
Максимальное значение центробежной силы будет на экваторе, где она равна примерно 3,4 Гал. Сила тяжести на поверхности Земли меняется в пределах от 978 до 983,2 Гал.
Потенциал центробежной силы равен:
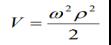
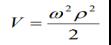
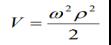
где ω - угловая скорость вращения Земли;
ρ - расстояние точки наблюдения от оси вращения
по нормали к ней.
Значение центробежной силы равно производной от потенциала V по ρ:
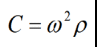
По известной величине географической широты точки наблюдения центробежная сила может быть вычислена с довольно высокой точностью. Но она никак не связана с распределением масс, т.е. с геологическими неоднородностями внутри земной коры и поэтому не несет в себе геологической информации.
Потенциал силы тяжести (или ускорения силы тяжести) равен сумме потенциалов ньютоновской силы притяжения и центробежной силы
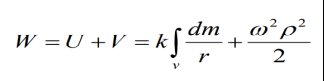
Потенциал W в отличии от потенциала U на бесконечности стремится к бесконечности а не к нулю, как потенциал притяжения, за счет центробежной силы. Но, учитывая, что гравиразведка изучает гравитационное поле на поверхности Земли, т.е. на конечном расстоянии от центра Земли, влияние этой составляющей силы тяжести учитывается при вычитании из наблюденных значений силы тяжести так называемого нормального поля, о чем будет сказано ниже.
Земля имеет сложную форму, которая определяется не только распределением масс в земной коре, но главным образом, распределением масс внутри мантии и астеносферы. При первом приближении Земля имеет форму шара. Но вследствие вращения, Земля имеет сжатие и сравнима с эллипсоидом (или сфероидом). Но и сжатие не полностью характеризует форму Земли. В1872 г. немецкий геодезист Листинг предложил за форму Земли принимать уровенную поверхность потенциала силы тяжести, совпадающую с поверхностью воды в океанах и открытых морях, которую он назвал геоидом. Геоид – это фигура, образуемая поверхностью морей и океанов в невозмущенном состоянии, а на континентах она определялась бы уровнем воды в системе соединяющихся между собой и с открытыми морями и океанами каналов. На практике, высоты земной поверхности определяются относительно уровня моря, т.е. геоида. Фигура геоида зависит от распределения масс внутри Земли, закон которого нам не известен, поэтому ее невозможно описать точной математической формулой. Но геоид может быть достаточно близко представлен в виде простой модели - сфероидом (или референц- эллипсоидом) для описания которого можно вывести точную математическую формулу. Значения силы тяжести, вычисленные для модели Земли (т.е. для земного сфероида), называются нормальными. Возможное взаимное расположение физической поверхности Земли, уровня геоида и теоретической Земли дано на нижерасположенном рисунке 3.
Р
ис.3. Возможное взаимное расположение поверхностей: 1 – физической Земли; 2 – геоида; 3 – теоретической Земли.
Плотность пород изменяется от поверхности к центру и в горизонтальном направлении. Вследствие этого и гравитационное поле Земли имеет сложный характер; его можно представить состоящим из двух частей: нормальной и аномальной. Нормальное поле соответствует модели Земли. В гравиразведке за модель Земли принимают двухосный эллипсоид вращения с параметрами, максимально соответствующими реальной Земле. Для задания потенциала гравитационного поля такой модели необходимо задать сжатие, величину экваториального радиуса, значение силы тяжести на экваторе и угловую скорость вращения Земли. Производная по нормали к поверхности референц-эллипсоида от его потенциала притяжения и представляет собой нормальное значение силы тяжести γ0 . В зависимости от исходных параметров земного сфероида получают различные числовые коэффициенты формулы нормального значения силы тяжести. В России принята формула Гельмерта, выведенная в 1901-1909 гг., для модели Земли в виде двухосного эллипсоида со сжатием 1/298,2 и с учетом результатов измерения силы тяжести на 1603 пунктах. Коэффициенты формулы были уточнены в 1978 году и в настоящее время формула Гельмерта имеет вид:
П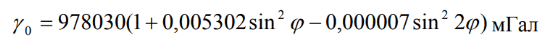
о этой формуле для любой точки поверхности модели Земли в зависимости от заданной географической широты пункта можно вычислить теоретическое значение силы тяжести. В мире существует несколько формул нормального значения силы тяжести (Сомильяна, Ф.Н.Красовского, Н.П.Грушинского, У.Уотиллы, У.Хейсканена и др.).
Введение понятия нормального значения силы тяжести необходимо для изучения внутреннего строения Земли с помощью гравиразведки. Алгоритм изучения Земли следующий. Производя измерения силы тяжести на физической поверхности Земли, сравнивая полученные результаты с теоретическими и интерпретируя отклонения силы тяжести мы можем уточнять строение модели. По мере увеличения детальности и точности измерений силы тяжести увеличивается детальность строения Земли. Измерения силы тяжести обычно производят на поверхности реальной, физической Земли. Высоты (альтитуды) пунктов измерения отсчитывают от поверхности уровня моря.
Часть II
2.1. Прямые и обратные задачи гравиразведки.
Основой теории интерпретации данных гравиразведки является решение прямых и обратных задач. Прямая задача гравиразведки состоит в определении элементов поля силы тяжести по заданному распределению его источников, когда известны форма, размеры, глубина залегания и величина эффективной плотности. Обратная задача гравиразведки ставит противоположную цель: нахождение параметров объекта (формы, размеров, глубины залегания, эффективной плотности) по известному распределению (на профиле или на площади) элементов силы тяжести.
Решение прямой задачи в общем виде. Аномалии силы тяжести, вызванные притяжением тел известной формы, размера и избыточной плотности, рассчитывают на основе закона всемирного тяготения (закона Ньютона).
Для этого притягивающее тело разбивают на элементарные массы (dm); рассчитывают аномалию такой точечной массы (Δg1), которая равна вертикальной составляющей силы (F1) ньютоновского притяжения этой массой массы, равной 1 г, находящейся в точке наблюдения А, т. е. берут составляющую силы притяжения по направлению действия силы тяжести Земли (g); наконец, используя принцип суперпозиции, определяют аномалию за счет притяжения всем телом (ΔgT) как сумму притяжений всех элементарных точечных масс
, которыми можно представить аномалообразующее тело.
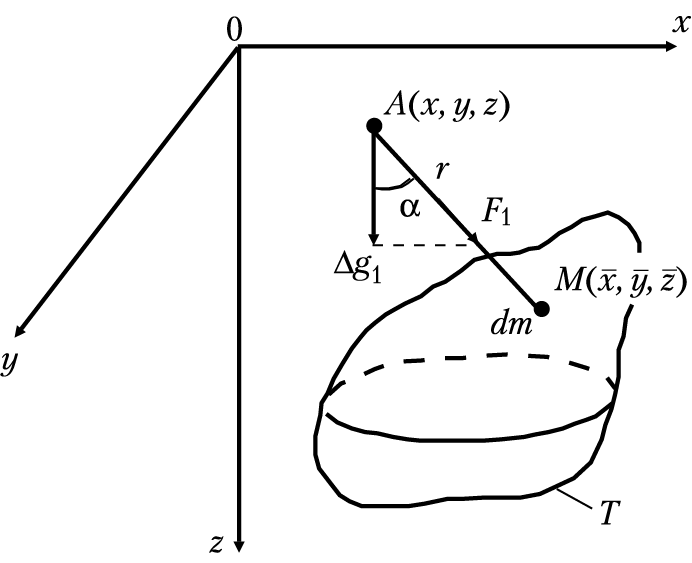
Рис. 4. Схема определения аномалий силы тяжести
от элементарной массы (dm) и гравитирующего тела (Т)
Математически это может быть выражено следующим образом:
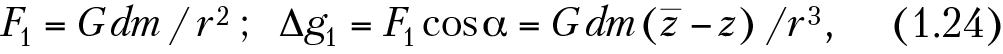
где r расстояние между точкой наблюдения А (х, у, z) и точкой, в которой находится элементарная точечная масса (dm). В природных условиях аномальные включения с плотностью σ находятся во вмещающей среде с плотностью σ0, поэтому под массой dm надо понимать избыточную массу: dm = (σ — σ0)dV = ΔσdV, где dV — элементарный объем точечной массы; Δσ — эффективная плотность.
Окончательные выражения для расчета аномалии силы тяжести точечной массы и тела, используемые в теории гравиразведки, имеют вид
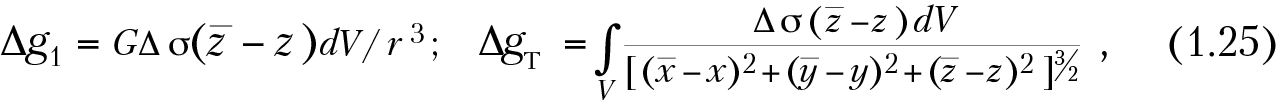
Интеграл в последней формуле берут по всему объему тела (V). При σ > σ0 значения ΔgT имеют положительный знак, т. е. наблюдаются увеличение притяжения и положительные аномалии. При σ < σ0 значения ΔgT имеют отрицательный знак, т. е. наблюдаются уменьшение притяжения и отрицательные аномалии.
Аналитические решения с помощью уравнения (1.25) получаются лишь для тел простой геометрической формы (шар, цилиндр и др.) с постоянным значением эффективной плотности. Для тел более сложной формы, особенно с переменной плотностью, возможны лишь численные решения интеграла (1.25) на основе сложных вычислительных схем. Анализ решений прямых задач служит основой при разработке приемов решения обратных задач гравиразведки для типовых геологических структур и объектов аналитическим методом.
Рассмотрим несколько примеров решения прямых и обратных задач для тел правильной геометрической формы.
2.2.Прямая и обратная задача для шара.
Пусть однородный шар радиусом R, объемом V, с избыточной плотностью Δσ расположен на оси Z на глубине h. Решим прямую задачу, т. е. определим гравитационный эффект вдоль наземного профиля ОХ, проходящего через проекцию центра шара с началом координат над ним. Поскольку по закону всемирного тяготения шар притягивается с такой же силой, что и точечная масса, сосредоточенная в его центре, аномалию над шаром (Δg
ш) можно получить без решения интеграла (1.25), считая, что аномалия силы тяжести над шаром и аномалия точечной массы, помещенной в его центре, совпадают:
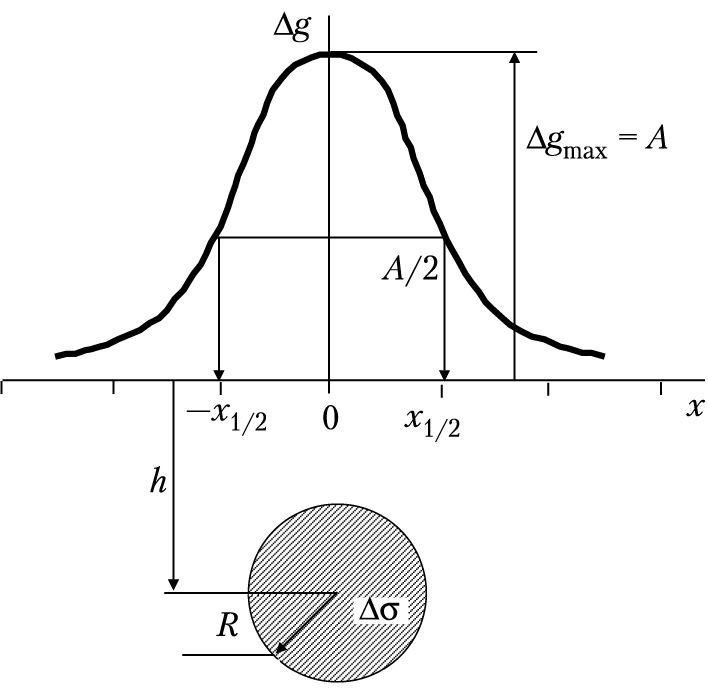
Рис. 5. Гравитационная аномалия (∆g(х)) от модели в виде шара
или горизонтального стержня (цилиндра) при Δσ > 0
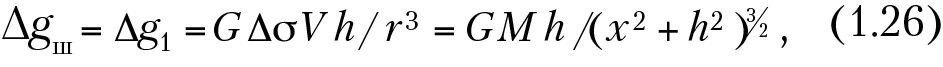
где M = ΔσV — эффективная масса шара.
График Δgш будет иметь максимум (при Δσ >0) над центром шара Δgmax(0) = GM/h2 = А и асимптотически стремиться к нулю при х → ± бесконечности. Знак Δgш определяется знаком Δσ. Если провести расчеты по ряду профилей, то очевидно, что карта изолиний Δgш будет иметь вид концентрических окружностей с центром над шаром, т. е. аномалия Δgш в плане на плоскости х0у будет изометричной.
Из анализа уравнения (1.26) и графиков на можно решить обратную задачу. Например, найдем абсциссу x1/2, в которой Δgш достигает половины максимума:

откуда (x21/2 + h2)3/2 = 2h3. Решив это уравнение, получим:
|x1/2| = 0,76 h или h = 1,31 |x1/2|.
Таким образом, определив по графику Δgш значения Δgmax, 1/2 ⋅ Δgmax и абсциссу точки кривой x1/2, где Δgш = 1/2 ⋅ Δgmax, и умножив ее на коэффициент 1,31, можно найти глубину залегания центра шарообразного объекта (h). Далее можно рассчитать эффективную массу (M = Δgmaxh2/G), а зная Δσ, определить радиус (R).
2.3. Прямая и обратная задачи для горизонтального кругового цилиндра.
Пусть горизонтальный бесконечно длинный круговой цилиндр радиуса R, сечения S, с избыточной плотностью ∆σ расположен вдоль оси у на глубине h.
Решим прямую задачу, т. е. определим ΔgГЦ вдоль оси х, направленной вкрест простирания цилиндра с началом координат над его центром. Притяжение цилиндра будет таким же, как притяжение вещественной линии, расположенной вдоль его оси с массой единицы длины dm = SΔσdy. Поэтому для точек наблюдения вдоль оси х (y = z = 0) с учетом того, что х = 0, –∞ < y < +∞ (цилиндр считается бесконечно длинным) и z = h, аналитическое выражение можно получить из уравнения (1.25):
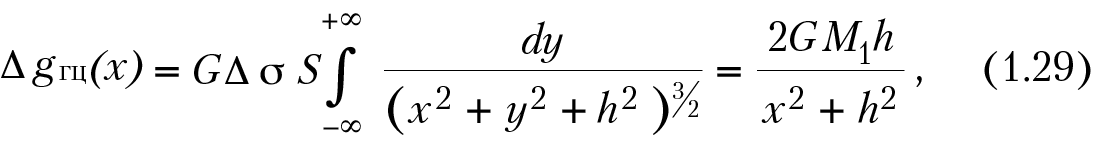
Р

ис. 2. Сила тяжести g равна векторной сумме ньютоновской силы притяжения F и центробежной силы С.
Центробежная сила уменьшает ньютоновскую силу притяжения. На полюсах Земли, где центробежная сила отсутствует, сила тяжести g максимальна. Увеличение силы тяжести на полюсах вызвано также уменьшением полярного радиуса Земли, примерно на 21 км вследствие ее сжатия, вызванного вращением последней, и равного примерно 1/298.24, что приводит к дополнительному увеличению силы тяжести еще примерно на 1,8 Гал.
Максимальное значение центробежной силы будет на экваторе, где она равна примерно 3,4 Гал. Сила тяжести на поверхности Земли меняется в пределах от 978 до 983,2 Гал.
Потенциал центробежной силы равен:
где ω - угловая скорость вращения Земли;
ρ - расстояние точки наблюдения от оси вращения
по нормали к ней.
Значение центробежной силы равно производной от потенциала V по ρ:
По известной величине географической широты точки наблюдения центробежная сила может быть вычислена с довольно высокой точностью. Но она никак не связана с распределением масс, т.е. с геологическими неоднородностями внутри земной коры и поэтому не несет в себе геологической информации.
Потенциал силы тяжести (или ускорения силы тяжести) равен сумме потенциалов ньютоновской силы притяжения и центробежной силы
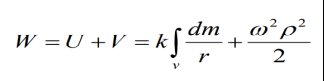
Потенциал W в отличии от потенциала U на бесконечности стремится к бесконечности а не к нулю, как потенциал притяжения, за счет центробежной силы. Но, учитывая, что гравиразведка изучает гравитационное поле на поверхности Земли, т.е. на конечном расстоянии от центра Земли, влияние этой составляющей силы тяжести учитывается при вычитании из наблюденных значений силы тяжести так называемого нормального поля, о чем будет сказано ниже.
Земля имеет сложную форму, которая определяется не только распределением масс в земной коре, но главным образом, распределением масс внутри мантии и астеносферы. При первом приближении Земля имеет форму шара. Но вследствие вращения, Земля имеет сжатие и сравнима с эллипсоидом (или сфероидом). Но и сжатие не полностью характеризует форму Земли. В1872 г. немецкий геодезист Листинг предложил за форму Земли принимать уровенную поверхность потенциала силы тяжести, совпадающую с поверхностью воды в океанах и открытых морях, которую он назвал геоидом. Геоид – это фигура, образуемая поверхностью морей и океанов в невозмущенном состоянии, а на континентах она определялась бы уровнем воды в системе соединяющихся между собой и с открытыми морями и океанами каналов. На практике, высоты земной поверхности определяются относительно уровня моря, т.е. геоида. Фигура геоида зависит от распределения масс внутри Земли, закон которого нам не известен, поэтому ее невозможно описать точной математической формулой. Но геоид может быть достаточно близко представлен в виде простой модели - сфероидом (или референц- эллипсоидом) для описания которого можно вывести точную математическую формулу. Значения силы тяжести, вычисленные для модели Земли (т.е. для земного сфероида), называются нормальными. Возможное взаимное расположение физической поверхности Земли, уровня геоида и теоретической Земли дано на нижерасположенном рисунке 3.
Р

ис.3. Возможное взаимное расположение поверхностей: 1 – физической Земли; 2 – геоида; 3 – теоретической Земли.
Плотность пород изменяется от поверхности к центру и в горизонтальном направлении. Вследствие этого и гравитационное поле Земли имеет сложный характер; его можно представить состоящим из двух частей: нормальной и аномальной. Нормальное поле соответствует модели Земли. В гравиразведке за модель Земли принимают двухосный эллипсоид вращения с параметрами, максимально соответствующими реальной Земле. Для задания потенциала гравитационного поля такой модели необходимо задать сжатие, величину экваториального радиуса, значение силы тяжести на экваторе и угловую скорость вращения Земли. Производная по нормали к поверхности референц-эллипсоида от его потенциала притяжения и представляет собой нормальное значение силы тяжести γ0 . В зависимости от исходных параметров земного сфероида получают различные числовые коэффициенты формулы нормального значения силы тяжести. В России принята формула Гельмерта, выведенная в 1901-1909 гг., для модели Земли в виде двухосного эллипсоида со сжатием 1/298,2 и с учетом результатов измерения силы тяжести на 1603 пунктах. Коэффициенты формулы были уточнены в 1978 году и в настоящее время формула Гельмерта имеет вид:
П
о этой формуле для любой точки поверхности модели Земли в зависимости от заданной географической широты пункта можно вычислить теоретическое значение силы тяжести. В мире существует несколько формул нормального значения силы тяжести (Сомильяна, Ф.Н.Красовского, Н.П.Грушинского, У.Уотиллы, У.Хейсканена и др.).
Введение понятия нормального значения силы тяжести необходимо для изучения внутреннего строения Земли с помощью гравиразведки. Алгоритм изучения Земли следующий. Производя измерения силы тяжести на физической поверхности Земли, сравнивая полученные результаты с теоретическими и интерпретируя отклонения силы тяжести мы можем уточнять строение модели. По мере увеличения детальности и точности измерений силы тяжести увеличивается детальность строения Земли. Измерения силы тяжести обычно производят на поверхности реальной, физической Земли. Высоты (альтитуды) пунктов измерения отсчитывают от поверхности уровня моря.
Часть II
2.1. Прямые и обратные задачи гравиразведки.
Основой теории интерпретации данных гравиразведки является решение прямых и обратных задач. Прямая задача гравиразведки состоит в определении элементов поля силы тяжести по заданному распределению его источников, когда известны форма, размеры, глубина залегания и величина эффективной плотности. Обратная задача гравиразведки ставит противоположную цель: нахождение параметров объекта (формы, размеров, глубины залегания, эффективной плотности) по известному распределению (на профиле или на площади) элементов силы тяжести.
Решение прямой задачи в общем виде. Аномалии силы тяжести, вызванные притяжением тел известной формы, размера и избыточной плотности, рассчитывают на основе закона всемирного тяготения (закона Ньютона).
Для этого притягивающее тело разбивают на элементарные массы (dm); рассчитывают аномалию такой точечной массы (Δg1), которая равна вертикальной составляющей силы (F1) ньютоновского притяжения этой массой массы, равной 1 г, находящейся в точке наблюдения А, т. е. берут составляющую силы притяжения по направлению действия силы тяжести Земли (g); наконец, используя принцип суперпозиции, определяют аномалию за счет притяжения всем телом (ΔgT) как сумму притяжений всех элементарных точечных масс
, которыми можно представить аномалообразующее тело.

Рис. 4. Схема определения аномалий силы тяжести
от элементарной массы (dm) и гравитирующего тела (Т)
Математически это может быть выражено следующим образом:
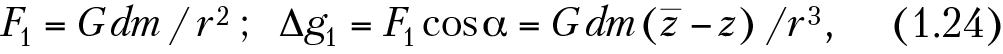
где r расстояние между точкой наблюдения А (х, у, z) и точкой, в которой находится элементарная точечная масса (dm). В природных условиях аномальные включения с плотностью σ находятся во вмещающей среде с плотностью σ0, поэтому под массой dm надо понимать избыточную массу: dm = (σ — σ0)dV = ΔσdV, где dV — элементарный объем точечной массы; Δσ — эффективная плотность.
Окончательные выражения для расчета аномалии силы тяжести точечной массы и тела, используемые в теории гравиразведки, имеют вид
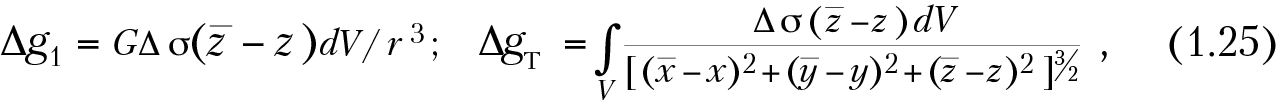
Интеграл в последней формуле берут по всему объему тела (V). При σ > σ0 значения ΔgT имеют положительный знак, т. е. наблюдаются увеличение притяжения и положительные аномалии. При σ < σ0 значения ΔgT имеют отрицательный знак, т. е. наблюдаются уменьшение притяжения и отрицательные аномалии.
Аналитические решения с помощью уравнения (1.25) получаются лишь для тел простой геометрической формы (шар, цилиндр и др.) с постоянным значением эффективной плотности. Для тел более сложной формы, особенно с переменной плотностью, возможны лишь численные решения интеграла (1.25) на основе сложных вычислительных схем. Анализ решений прямых задач служит основой при разработке приемов решения обратных задач гравиразведки для типовых геологических структур и объектов аналитическим методом.
Рассмотрим несколько примеров решения прямых и обратных задач для тел правильной геометрической формы.
2.2.Прямая и обратная задача для шара.
Пусть однородный шар радиусом R, объемом V, с избыточной плотностью Δσ расположен на оси Z на глубине h. Решим прямую задачу, т. е. определим гравитационный эффект вдоль наземного профиля ОХ, проходящего через проекцию центра шара с началом координат над ним. Поскольку по закону всемирного тяготения шар притягивается с такой же силой, что и точечная масса, сосредоточенная в его центре, аномалию над шаром (Δg
ш) можно получить без решения интеграла (1.25), считая, что аномалия силы тяжести над шаром и аномалия точечной массы, помещенной в его центре, совпадают:

Рис. 5. Гравитационная аномалия (∆g(х)) от модели в виде шара
или горизонтального стержня (цилиндра) при Δσ > 0
где M = ΔσV — эффективная масса шара.
График Δgш будет иметь максимум (при Δσ >0) над центром шара Δgmax(0) = GM/h2 = А и асимптотически стремиться к нулю при х → ± бесконечности. Знак Δgш определяется знаком Δσ. Если провести расчеты по ряду профилей, то очевидно, что карта изолиний Δgш будет иметь вид концентрических окружностей с центром над шаром, т. е. аномалия Δgш в плане на плоскости х0у будет изометричной.
Из анализа уравнения (1.26) и графиков на можно решить обратную задачу. Например, найдем абсциссу x1/2, в которой Δgш достигает половины максимума:

откуда (x21/2 + h2)3/2 = 2h3. Решив это уравнение, получим:
|x1/2| = 0,76 h или h = 1,31 |x1/2|.
Таким образом, определив по графику Δgш значения Δgmax, 1/2 ⋅ Δgmax и абсциссу точки кривой x1/2, где Δgш = 1/2 ⋅ Δgmax, и умножив ее на коэффициент 1,31, можно найти глубину залегания центра шарообразного объекта (h). Далее можно рассчитать эффективную массу (M = Δgmaxh2/G), а зная Δσ, определить радиус (R).
2.3. Прямая и обратная задачи для горизонтального кругового цилиндра.
Пусть горизонтальный бесконечно длинный круговой цилиндр радиуса R, сечения S, с избыточной плотностью ∆σ расположен вдоль оси у на глубине h.
Решим прямую задачу, т. е. определим ΔgГЦ вдоль оси х, направленной вкрест простирания цилиндра с началом координат над его центром. Притяжение цилиндра будет таким же, как притяжение вещественной линии, расположенной вдоль его оси с массой единицы длины dm = SΔσdy. Поэтому для точек наблюдения вдоль оси х (y = z = 0) с учетом того, что х = 0, –∞ < y < +∞ (цилиндр считается бесконечно длинным) и z = h, аналитическое выражение можно получить из уравнения (1.25):