Файл: Практическое задание 1 по учебному курсу Физика. Механика.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.11.2023
Просмотров: 19
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
 МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИфедеральное государственное бюджетное образовательное учреждение высшего образования
«Тольяттинский государственный университет»
Институт химии и энергетики
| (наименование института полностью) |
| Кафедра "Электроснабжение и электротехника" |
| (Наименование учебного структурного подразделения) |
| 13.03.02 Электроэнергетика и электротехника |
| (код и наименование направления подготовки / специальности) |
| Электроснабжение |
| (направленность (профиль) / специализация) |
Практическое задание 1
по учебному курсу «Физика. Механика. Молекулярная физика»
(наименование учебного курса)
Вариант 13 (при наличии)
| Обучающегося | Ямилев Е. В. | |
| | (И.О. Фамилия) | |
| Группа | ЭЭТбп-2201а | |
| | | |
| Преподаватель | Потемкина С. Н. | |
| | (И.О. Фамилия) | |
Тольятти 2023
Задание1
Задача 1
Частица движется равноускоренно в координатной плоскости XY с
начальной скоростью
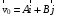 и ускорением
и ускорением 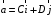 .
.Найти модули векторов скорости v , тангенциального
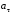
и нормального
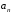 ускорений, а также радиус кривизны траектории R в момент времени t .
ускорений, а также радиус кривизны траектории R в момент времени t .Дано: вар.13 А = -1 м/с, В = 2 м/с, С = 0, D= -3 м/с2, t = 2 с
Решение:
Применяем закон независимости движений: раскладываем движение по осям координат и анализируем их отдельно. Проекции начальной скорости (м/с)
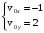 (1)
(1) Проекции ускорения (м/с2)
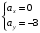 (2)
(2)Модуль ускорения
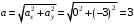 м/с2
м/с2 (не зависит от времени)
Проекции скоростей в момент t = 2 с
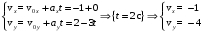 м/с
м/сМодуль скорости
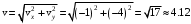 м/с
м/сПо определению тангенциальное (касательное) ускорение равно производной от модуля скорости по времени
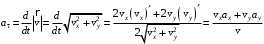
вычисляем для t = 2 с
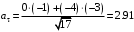 м/с2
м/с2Нормальное ускорение
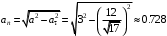 м/с2
м/с2Радиус кривизны траектории
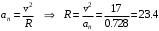 м
м Ответ:
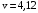 м/с
м/с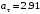 м/с2
м/с2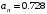 м/с2
м/с2 R= 23,4 м
Задача 2
На однородный цилиндрический блок массой т2и радиусом Rнамотана невесомая нить, к свободному концу которой прикреплен груз массой т1.
К блоку крестообразно прикреплены четыре одинаковых невесомых стержня, на которых закреплены одинаковые грузы массой т3на расстоянии хот оси вращения. Грузы т3 можно считать материальными точками. Трением в блоке можно пренебречь. Найти зависимость ускорения агруза т1, от
расстояния х. Построить график этой зависимости в интервале изменения х от Rдо 3R. Ускорение свободного падения g =9.81 м/с2.
Дано: вар 13. R = 0,2 м, т1 = 2 кг, т2 = 2 кг, т3 = 2 кг
Найти а(х)
Решение:
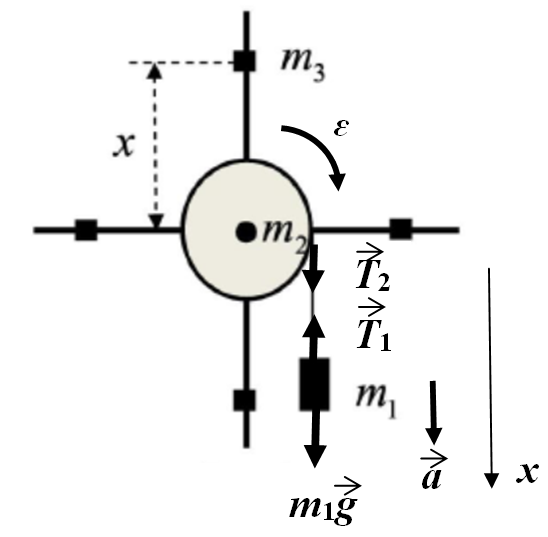
На чертеже показаны силы, действующие на каждое тело: сила тяжести m1g, силы натяжения нити T1 и T2 , которые будут одинаковы по величине
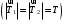 , но приложены к разным телам.
, но приложены к разным телам. Зададим положительное направление оси Xвниз и будем составлять уравнение движения согласно законам Ньютона
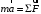 в проекции на эту ось.
в проекции на эту ось. Для блока запишем закон динамики вращения.
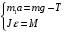 (1)
(1) а – ускорение груза, J – момент инерции блока, ε - угловое ускорение, T– сила натяжения нити, g - ускорение ободного падения, m1 – масса груза, М - момент силы.
Добавим к этим уравнениям связь между угловым ускорением блока ε и линейным ускорением груза а:
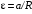 , и выражение для момента силы:
, и выражение для момента силы: 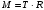 , R – радиус блока.
, R – радиус блока.Подставляем эти связи в систему уравнений (1) и решаем её относительно ускорения а.
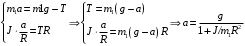 (2)
(2)Теперь определяем момент инерции системы. Он складывается из момента инерции блока
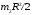 плюс момент инерции 4-х грузов (материальных точек)
плюс момент инерции 4-х грузов (материальных точек) 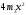
Итак,
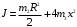 (3)
(3)Получаем окончательно
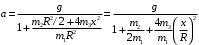 (4)
(4)подставим исходные данные
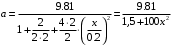 (5)
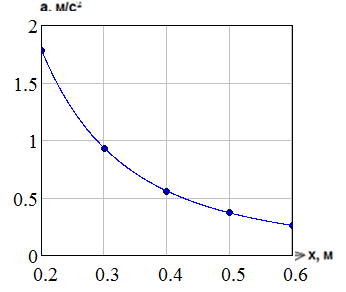
(5)таблица значений для графика
| х, м | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 |
| а, м/с2 | 1.78 | 0.93 | 0.56 | 0.37 | 0.26 |
График а(х)
Задача 3
Шар массой т1, летящий со скоростью v1 сталкивается с неподвижным шаром массой т2. После удара шары разлетаются под углом α друг к другу. Удар абсолютно упругий, столкновение происходит в горизонтальной плоскости. Найти скорости
шаров и1 и и2после удара.
Дано: вар. 13. т1 = 0,25 кг, v1 = 20 м/с, т2 = 0,10 кг, v2 = 0, α = 600
Найти: и1, и2
Решение
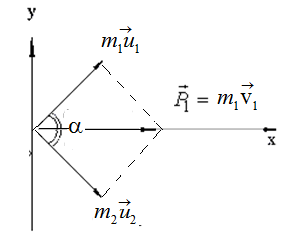
Запишем закон сохранения импульса в векторной форме
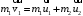 (1)
(1)Возведём в квадрат обе части уравнения (1). При этом учтём, что скалярное произведение
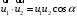 . Получим уравнение для импульсов
. Получим уравнение для импульсов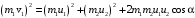 (2)
(2)Второе уравнение – это закон сохранения кинетической энергии (удар абсолютно упругий). Множитель 1/2 сокращаем
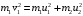 (3)
(3)Решаем систему. Уменьшим число переменных, введя отношение масс
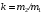 и вычтем уравнения, тогда
и вычтем уравнения, тогда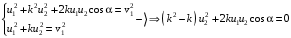 (4)
(4)Из последнего уравнения выражаем
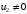 подставляем во второе
подставляем во второе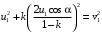 (5)
(5) Из (4) выражаем u1, оставляем только положительный корень
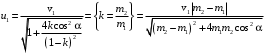 (6)
(6)Теперь из (4)
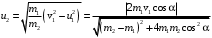 (7)
(7)вычисляем
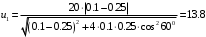 м/с
м/с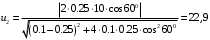 м/с
м/сПроверим решение по второму уравнению системы
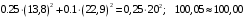 верно с учётом погрешности приближённых вычислений.
верно с учётом погрешности приближённых вычислений.Ответ: скорости шаров после удара и1 = 13,8 м/с, и2 = 22,9 м/с