ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.11.2023
Просмотров: 886
Скачиваний: 15
СОДЕРЖАНИЕ
БӚЛІМ БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУҒА АРНАЛҒАН ТАПСЫРМАЛАР Алгебра
«Екі айнымалысы бар теңдеулер,теңсіздіктер және олардың жүйелері»
Бағалау критерииі: Білім алушы:
Бағалау критерииі: Білім алушы:
ТОҚСАН БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУҒА АРНАЛҒАН ТАПСЫРМАЛАР
ТОҚСАН БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУҒА АРНАЛҒАН ТАПСЫРМАЛАР
ТОҚСАН БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУҒА АРНАЛҒАН ТАПСЫРМАЛАР
«Ықтималдықтар теориясының элементтері»
ТОҚСАН БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУҒА АРНАЛҒАН ТАПСЫРМАЛАР
ТОҚСАН БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУҒА АРНАЛҒАН ТАПСЫРМАЛАР
ТОҚСАН БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУҒА АРНАЛҒАН ТАПСЫРМАЛАР
ТОҚСАН БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУ СПЕЦИФИКАЦИЯСЫ
ТОҚСАН БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУ СПЕЦИФИКАЦИЯСЫ
Барлығы 20 балл



 I нұсқа
I нұсқа| № | Жауап | Балл | Қосымша ақпарат | ||
| 1 | (⃗B⃗⃗⃗A⃗→ ; ⃗A⃗⃗⃗????⃗→) = (⃗B⃗⃗⃗A⃗→ ; ⃗B⃗⃗⃗⃗C→) | 1 | | ||
| 180-126=54; С | 1 | ||||
| 2 | Жіктеуі бойынша вектордың координасын жазады (-3;6), (2;-2) | 1 | Балама тәсіл қабылданады | ||
| Векторларға координалар арқылы амалдар қолданып, вектордың координатасын табады (-3;4) | 1 | ||||
| Вектордың ұзындығын табады 5 | 1 | ||||
| 3 | ⃗A⃗⃗⃗B⃗→ − ⃗????⃗⃗⃗????⃗→ = ????⃗⃗⃗⃗⃗????⃗→ | 1 | | ||
| ????⃗⃗⃗⃗⃗????⃗→ + ????⃗⃗⃗⃗????⃗→ = ⃗????⃗⃗⃗????⃗→ | 1 | ||||
| 4 | ⃗ ⃗⃗⃗⃗ ⃗→ =(2;-4) және ⃗ ⃗⃗⃗⃗????⃗→ = (3; ???? − 1) координатасын табады | 1 | Балама тәсіл қабылданады | ||
| Векторлардың коллинеарлық шартын қолданып пропорция құрастырады 2 = −4 3 ????−1 | 1 | ||||
| Теңдеуді шешіп, b=-5 табады | 1 | ||||
| Векторладың перпендикулярлық шартын қолданып векторлардың скаляр кӛбейтіндісі арқылы теңдеу жазады 6-4(b-1)=0 | 1 | ||||
| Теңдеуді шешіп, b=2,5 екенін табады. | 1 | ||||
| 5 | Бұрыштан шығатын векторларды анықтап,олардың координаталарын табады (6;-9), (9;-7) | 1 | | ||
| Вектордың скаляр кӛбейтіндісін есептейді 117 | 1 | ||||
  векторлардың модулін есептейді √11 √130 | 1 | ||||
| векторлардың скаляр кӛбейтіндісінің формуласын қолданып, векторлардың арасындағы бұрышты  есептеп табады √11 130 | 1 | ||||
| 6 | Қысқаша кӛбейту формуласын қолданып ӛрнекті ықшамдайды ????⃗⃗⃗⃗????⃗→2 − 6????⃗⃗⃗⃗????⃗→ · ????⃗⃗⃗⃗????⃗→ + 9⃗????⃗⃗⃗????⃗→2 | 1 | Балама тәсіл қабылданады | ||
| Үшбұрыштың қабырғасын табады 18: 3=6 және скаляр квадраттың қасиетін қолданады ????⃗⃗⃗⃗????⃗→2 = ????⃗⃗⃗⃗????⃗→2 = 36 | 1 | ||||
| Тең қабырғалы үшбұрыштың бұрыштары 60° болатынын ескере отырып вектордың скаляр кӛбейтіндісін есептеп табады ????⃗⃗⃗⃗????⃗→ · ⃗????⃗⃗⃗????⃗→ = 6 · 6 · 1=18 2 | 1 | ||||
| Ӛрнектің мәнін есептейді 36 6*18+9*36=252 | 1 | ||||
| Барлық балл: | 20 | | |||



 IІ нұсқа
IІ нұсқа | № | Жауап | Балл | Қосымша ақпарат |
| 1 | (⃗B⃗⃗⃗⃗C→ ; ⃗C⃗⃗⃗????⃗→) = (⃗B⃗⃗⃗⃗C→ ; ⃗B⃗⃗⃗A⃗→) | 1 | |
| 180-60=120; Е | 1 | ||
| 2 | Жіктеуі бойынша вектордың координасын жазады (3;-2), (-6;2) | 1 | Балама тәсіл қабылданады |
| Векторларға координалар арқылы амалдар қолданып, вектордың координатасын табады (-6;3) | 1 | ||
  Вектордың ұзындығын табады √45 = 3√5 | 1 | ||
| 3 | ????⃗⃗⃗⃗????⃗→ − ????⃗⃗⃗⃗????⃗→ = B⃗⃗⃗⃗????⃗→ | 1 | |
| B⃗⃗⃗⃗????⃗→ + ⃗????⃗⃗⃗????⃗→ = ????⃗⃗⃗⃗????⃗→ | 1 | ||
| 4 | B a a a a a ⃗????⃗⃗⃗????⃗→ =(-6;4) және ⃗????⃗⃗⃗????⃗→ = (−4; ???? + 1) | 1 | Балама тәсіл қабылданады |
| Векторлардың коллинеарлық шартын қолданып пропорция құрастырады −6 = 4 −4 ????+1 | 1 | ||
| Теңдеуді шешіп, a=5 = 1 2 табады 3 3 | 1 | ||
| Векторладың перпендикулярлық шартын қолданып векторлардың скаляр кӛбейтіндісі арқылы теңдеу жазады 24+4(a+1)=0 | 1 | ||
| Теңдеуді шешіп, a=-7 теңдеуді шешіп. | 1 | ||
| 5 | Бұрыштан шығатын векторларды анықтап,олардың координаталарын табады (-1;1), (-2;5) | 1 | |
| Вектордың скаляр кӛбейтіндісін есептейді 7 | 1 | ||
  векторлардың модулін есептейді √2 √29 | 1 | ||
| векторлардың скаляр кӛбейтіндісінің формуласын қолданып, векторлардың арасындағы бұрышты есептеп табады 7 √58 | 1 | ||
| 6 | Қысқаша кӛбейту формуласын қолданып ӛрнекті ықшамдайды 4????⃗⃗⃗⃗????⃗→2 + 12????⃗⃗⃗⃗????⃗→ · ⃗????⃗⃗⃗????⃗→ + 9????⃗⃗⃗⃗????⃗→2 | 1 | Балама тәсіл қабылданады |
| Үшбұрыштың қабырғасын табады 20: 4=5 және скаляр квадраттың қасиетін қолданады ????⃗⃗⃗⃗????⃗→2 = ⃗????⃗⃗⃗????⃗→2 = 25 | 1 | ||
| Тең қабырғалы үшбұрыштың бұрыштары 60° болатынын ескере отырып вектордың скаляр кӛбейтіндісін есептеп табады ????⃗⃗⃗⃗????⃗→ · ⃗????⃗⃗⃗????⃗→ = 5 · 5 · 0 = 0 | 1 | ||
| Ӛрнектің мәнін есептейді 325 | 1 | ||
| Барлық балл: | 20 | | |
- 1 ... 32 33 34 35 36 37 38 39 ... 44
ТОҚСАН БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУ СПЕЦИФИКАЦИЯСЫ
Ұзақтығы 40 минут
I нұсқа
-
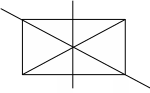 [3 балл] ABCD –тіктӛртбұрыш,N нүктесі AD қабырғасының ортасы. Дұрыс тұжырымды белгіле:
[3 балл] ABCD –тіктӛртбұрыш,N нүктесі AD қабырғасының ортасы. Дұрыс тұжырымды белгіле:
-
В нүктесі D нүктесіне О нүктесі арқылы симметриялы b а -
О
В нүктесі D нүктесіне а түзуі арқылы симметриялы В С -
В нүктесі D нүктесіне b түзуі арұылы симметриялы -
А нүктесі D нүктесіне а түзуі арқылы симметриялы -
А нүктесі D нүктесіне О нүктесі арқылы симметриялы -
А нүктесі D нүктесіне N нүктесіне симметриялы
енің
ол
А N D
-
[1 балл] Р(-6; 8) нүктесіне абцисса осі арқылы симметриялы б атын нүкт координатасын табыңыз -
[1 балл] Қай тұжырым дұрыс?
А: Ромбының екі симметрия осі бар,олар оның диагональдары.
В: Ромбының екі симметрия осі бар, олар оның қабырғаларының екі орта перпендикулярлары
C: Ромбының тӛрт симметрия осі бар. D: Барлық тұжырым дұрыс емес.
-
[2 балл] ABC үшбұрышы A1B1C1 үшбұрышына гомотетиялы. AB=7 см, BC=18 см, AC= 23 см. A1B1C1 үшбұрышының кіші қабырғасын табыңыз, егер оның үлкен қабырғасы 115 см тең болса
-
[4 балл] ABC үшбұрышында AD биссектрисасы жүргізілген.Егер АС = 4; DC = 2; BD = 3-ке тең болса, ABC үшбұрышының периметр табыңыз.
-
[4 балл] АВС үшбұрышында АС қабырғасына параллель түзу АВ және ВС қабырғаларын сәйкес М және N нүктелерінде қиып ӛтеді. NС қабырғасын табыңыз, егер АС=69, МN=23, ВN=60 тең болса.
-
[2 балл] Параллель кӛшіруде А(–3; 4) нүктесі А1(1; –1)нүктесіне кӛшеді.В(2; –3) нүктесі параллель кӛшіру арқылы B1 нүктесіне кӛшсе B1 нүктесінің координатасын табыңыз.
8.[1 балл] АВСDромб салыңыз.АСвекторы арқылы параллель бейнеленген ромбыны салыңыз.
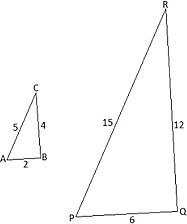 9. [2 балл] Суреттегі екі үшбұрыштың ұксас екенін кӛрсетіңіз.
9. [2 балл] Суреттегі екі үшбұрыштың ұксас екенін кӛрсетіңіз.