ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.12.2023
Просмотров: 18
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
15 режимы движения поезда
Различают три основных режима движения поезда: тяга, выбег и торможение. В режиме тяги (контроллер включен) на поезд действуют сила тяги локомотива и силы сопротивления движению, при выбеге (контроллер выключен), поезд движется по инерции в режиме торможения, на поезд действует как сила торможения, так и силы сопротивления движению. Сила инерции проявляет себя во всех случаях изменения режима движения поезда.
16 равнодействующая сила в режиме тяги
Величина и направление равнодействующей силы определяют движение поезда. Если равнодействующая сила больше нуля и имеет то же направление, что и движение, она его ускоряет. При знаке минус равнодействующая сила меньше нуля, направлена против движения и замедляет его. Равнодействующая сила, равная нулю, соответствует равномерному движению поезда либо стоянке. Соответственно равнодействующую силу называют ускоряющей (F - W), либо замедляющей [- Ь>и-(W + B)].
В режиме тяги удельная тормозная сила Ь, равна нулю и поезд движется с ускорением, пропорциональным равнодействующей силе, представляющей собой в зависимости от направления уклона (подъем или спуск) сумму или разность удельной силы тяги и сопротивления движению. Если равнодействующая сила практически не меняется, то движение происходит равноускоренно или равнозамедленно в зависимости от направления силы, т.е. с постоянным ускорением. В том случае, когда удельные силы тяги и сопротивления движению равны, движение поезда происходит с равномерной скоростью. Каждому значению приведенного уклона соответствует определенное значение равномерной (равновесной) скорости.
17 равнодействующая сила в режиме холостого хода
Величина и направление равнодействующей силы определяют движение поезда. Если равнодействующая сила больше нуля и имеет то же направление, что и движение, она его ускоряет. При знаке минус равнодействующая сила меньше нуля, направлена против движения и замедляет его. Равнодействующая сила, равная нулю, соответствует равномерному движению поезда либо стоянке. Соответственно равнодействующую силу называют ускоряющей (F - W), либо замедляющей [- Ь>и-(W + B)].
При движении на выбеге удельные силы тяги /к и торможения Ьт равны нулю. В этом случае равнодействующая равна удельной силе сопротивления движению tvK и поезд движется ускоренно или замедленно в зависимости от направления уклона (подъем или спуск).
18. равнодействующая сила в режиме торможения
Величина и направление равнодействующей силы определяют движение поезда. Если равнодействующая сила больше нуля и имеет то же направление, что и движение, она его ускоряет. При знаке минус равнодействующая сила меньше нуля, направлена против движения и замедляет его. Равнодействующая сила, равная нулю, соответствует равномерному движению поезда либо стоянке. Соответственно равнодействующую силу называют ускоряющей (F - W), либо замедляющей [- Ь>и-(W + B)].
При тормозном режиме удельная сила тяги равна нулю. В этом случае ускорение поезда пропорционально равнодействующей силе, равной сумме или разности удельных сил тормозной Ьт и сопротивления движению wK, которая меняет свое направление в зависимости от того, движется поезд по спуску или подъему.
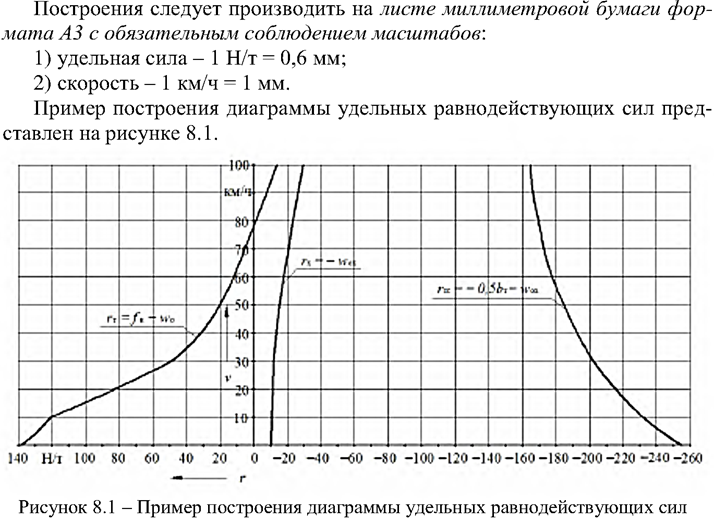
19 диаграмма удельных равнодействующих сил поезда
Тяга поездов – это отраслевая наука, изучающая управляемое движение поездов. Основной задачей теории тяги является исследование и расчет движущегося поезда. Процесс движения поезда по участку характеризуется тремя режимами работы локомотива: тяга, выбег (холостой ход) и торможение.
Режим тяги. Движение происходит с работающими тяговыми двигателями локомотива (применительно к электровозам и тепловозам – с электрической передачей), на поезд действуют сила тяги локомотива Fк и сила основного сопротивления движению (в режиме) Wо. Равнодействующая сила R=Fк-Wо.
Режим выбега. Движение происходит с выключенными тяговыми двигателями, на поезд действует основное сопротивление движению (в режиме выбега) Wх. Равнодействующая сила R=-Wx.
Режим торможения. В этом случае на поезд действует основное сопротивление движению (в режиме выбега) Wx и тормозная сила Bт. Равнодействующая сила R=-(Wx+Bт).
Характер движения поезда определяется величиной и направлением равнодействующей силы. Если равнодействующая сила равна нулю, то имеет место равномерное движение поезда (или стоянка), если больше нуля – ускоренное, если меньше нуля – замедленное. Движение поезда по железнодорожному участку отражено в виде дифференциального уравнения, которое устанавливает зависимость скорости, длины пройденного пути и времени движения от величины действующих на поезд сил.
Уравнение движения поезда в режиме тяги имеет вид:
(2.17)
Уравнение движения поезда в режиме холостого хода имеет вид:
(2.18)
Уравнение движения поезда в режиме служебного торможения имеет вид:
(2.19)
Величины, входящие в формулы (2.17) – (2.19) обозначают:
- ускорение поезда;
- коэффициент ускорения поезда;
fк – удельная сила тяги;
wo, wx – удельная сила естественного сопротивления движению в режиме тяги и выбега соответственно;
bт – удельная сила торможения.
Для построения диаграмм необходимо предварительно рассчитать величины удельных равнодействующих сил для режимов тяги, холостого хода и служебного торможения. Расчеты ведутся на ЭВМ, в которую вводится информация из макета данных. Макет данных (табл. 2.3) включает 15 строк, заполненных следующим образом:строки 1-13, 14 – заполняются согласно бланку задания и п.1,2; строка 15 – заполняется на основе тяговой характеристики локомотива.
20 спрямление продольного профиля пути
Для повышения точности результатов тяговых расчетов, а также для сокращения объема последних и, следовательно, времени на их выполнение, необходимо спрямлять профиль пути.
В процессе спрямления необходимо учитывать следующие ограничения.
Запрещается спрямлять:
- элементы станций и остановочных пунктов с соседними элементами (внутри станций элементы профиля пути спрямлять можно);
- элемент профиля расчетного подъема с соседними элементами;
- элементы профиля, на которых расположены максимальный спуск или подъем с соседними элементами;
- элементы профиля разного знака.
Спрямление профиля состоит в замене двух или нескольких смежных элементов продольного профиля пути одним элементом, длина которого sc равна сумме длин спрямляемых элементов (s1, s2, …,sn), т.е.
sc = s1+s2+…+sn, (1.1)
а общая крутизна спрямляемых элементов вычисляется по формуле
= , (1.2)
где …, - крутизна элементов спрямляемого участка.
21 (28)решение тормозной задачи
Поскольку режим торможения является важнейшим в обеспечении безопасности движения поездов, тормозным расчетам уделяют большое внимание. При расчетах используются следующие характеристики и переменные:
длина тормозного пути Sт;
наличие тормозных средств в поезде, определяемых расчетным тормозным коэффициентом ;
начальной vн и конечной vк скоростями движения;
уклонами i (конечную скорость принимают равной нулю).
Из этих пяти параметров определяют один по четырем заданным, используя аналитический или графический метод решения уравнения движения поезда. В зависимости от того, какую величину из пяти определяют, тормозные задачи подразделяют на три типа.
Первый тип тормозных задач или просто - первая тормозная задача - сводится к определению длины тормозного пути по заданным значениям vн, vк, и i.
Во втором типе рассчитывают допустимые скорости движения vн на различных уклонах i, исходя из условия остановки поезда в пределах заданного тормозного пути Sт, при заданном значении .
В третьем типе определяют, сколько тормозных средств нужно иметь в поезде (или какой должен быть ), чтобы поезд, движущийся с заданной скоростью vн, можно было остановить на заданном уклоне i в пределах тормозного пути Sт.
Первые две задачи называют задачами первого рода, третью задачу называют задачей второго рода. Наиболее часто приходится решать первую задачу по ограничению скоростей движения поездов на крутых спусках. Вторую задачу решают чаще всего при проверке эффективности действия тормозного оборудования поезда. Третью задачу решают при разработке новых конструкций подвижного состава, например поездов для скоростных пассажирских перевозок.