Жаттығу.

Қолда бар деректерге сәйкес, ол қажет:

1. Статистикалық таралу қатарын құрыңыз, алынған қатарды гистограмма арқылы графикалық түрде көрсетіңіз. Бөлу функциясын табыңыз, оның графигін құрыңыз.

2. Табыңыз: таңдаманың орташа мәні, таңдау дисперсиясы, таңдама стандартты ауытқуы, режим және медиана.

3. р = 0,05 мәнділік деңгейінде медиананың орташа таңдаманың шынайы мәніне сәйкестігі туралы гипотезаны тексеру үшін.

Варианттар



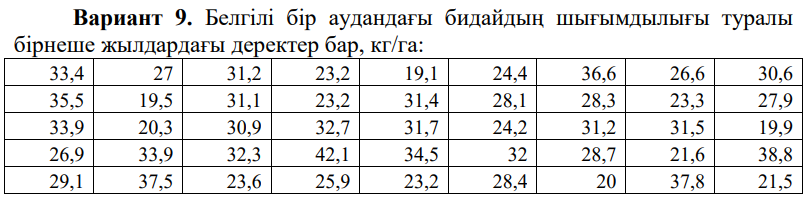
Шешім.

1. Нәтижедегі n = 45 таңдамалы жиынтық үшін:

а). Біз үлгі деректердің рейтингін орындаймыз.

19,1	19,5	19,9	20	20,3	21,5	21,6	23,2	23,2
23,2	23,3	23,6	24,2	24,4	25,9	26,6	26,9	27
27,9	28,1	28,3	28,4	28,7	29,1	30,6	30,9	31,1
31,2	31,2	31,4	31,5	31,7	32	32,3	32,7	33,4
33,9	33,9	34,5	35,5	36,6	37,5	37,8	38,8	42,1

б) Ерекшеліктің ең кіші және ең үлкен мәнін анықтаңыз.

X min 19.1

X max 42.1

в) Ерекшеліктің өзгеру диапазонын табыңыз

R Xmax-Xmin23

г) Таңдамалы жиынтықты бөлетін топтардың санын анықтау (ең жақын бүтін санға дейін дөңгелектеу)

k=1+3,32lg(45)=6,48≈6

д) Формула бойынша аралық ұзындығын анықтаңыз

h = R / k = 23/6 =3,28

е) Интервалдардың шекарасын анықтап, сәйкес интервалдар бойынша мәліметтерді топтаңыз ( ai ,bi ), i=1,2,…,k ,интервалдарының шекаралары келесі түрде алынады.

a₁ = X_min ; a _i+1 = b_i = a_i + h ; bk = xmax .

Топтастыру процесінде a_i < x ≤ b_i теңсіздіктерін қанағаттандыратын нұсқалар санын анықтаймыз және кестені толтыру арқылы интервалдық вариациялық қатарды тұрғызамыз

---

Таблица 1 – Интервалдарға бөлу

№ интервала	Границы интервала ai -bi	Частота mi	Накопленная частота i m i
1	19.1-22.38	3	3
2	22.38-25,66	5	8
3	25,66-28,94	10	18
4	28,94-32,22	14	32
5	32,22-35,5	10	42
6	35.5-38,78	6	48
k=7	38,78-42,1	2	50
	-	50	-

ж) Алынған мәліметтер негізінде статистикалық таралу қатарын және оның геометриялық кескіндерін саламыз.

Әрбір аралықта біз функцияның барлық мәндерін оның орташа мәніне теңестіреміз 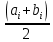және жиілік дәл осы мәнге қатысты деп есептейміз

№ Интер вала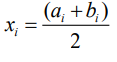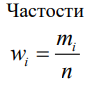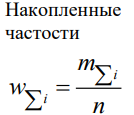
1	2.1-23.1	12.6	0.06	0.06	2.8*10-3
2	23.1-44.1	33.6	0.1	0.16	4.7*10-3
3	44.1-65.1	54.6	0.2	0.36	9.5*10-3
4	65.1-86.1	75.6	0.28	0.64	13.3*10-3
5	86.1-107.1	96.6	0.2	0.84	9.5*10-3
6	107.1-128.1	117.6	0.12	0.96	5.7*10-3
7	128.1-149.1	138.6	0.04	1	1.9*10-3
	-	-	1	-	-

---

---

Смотрите также файлы

• Тоо Макиза Структурное подразделение Все структурное подразделение.docx

• Жасанды интеллект Педагогті Т. А..docx

• Практическая работа по дисциплине оказание юридической помощи населению.docx

• План работы пришкольного летнего лагеря Солнышко кгу Калиновская средняя школа.docx

• Учебник для вузов. М Издво мгту им. Баумана, 2002, 336 с. Теоретические основы сапр Учебник для вузов Корячко В. П., Корейчик В. М., Норенков И. П. М. Энергоатомиздат, 1987, 400 с.doc