Дисциплина/МДК: ОП.02 Техническая механика

Специальность: 08.02.03 Производство неметаллических

строительных изделий и конструкций

Курс, группа: 2, 23 ПНСИК

Преподаватель: Кованёва Людмила Васильевна

Обратная связь: lkovanova1982@gmail.com

Дата: 10 апреля 2023 г.
Занятие № 4

Инструкция для обучающегося:

1. 
   Изучите материал лекции, особое внимание уделите формулам и рисункам.
   
2. 
   Составьте конспект лекции.
   
3. 
   Ответьте на вопросы для самоконтроля.
   
4. 
   Сроки предоставления выполненной работы на проверку: до следующего занятия
   

ТЕМА ЗАНЯТИЯ: Балки и балочные системы. Простые балки на двух опорах. Консоли. Шарнирно-консольные балки. Понятие о статически неопределимых балках

Цель: изучить балки и балочные системы, понятие о статически неопределимых балках.
План:

1. 
   Балки и балочные системы.
   
2. 
   Простые балки на двух опорах.
   
3. 
   Консоли.
   
4. 
   Шарнирно-консольные балки.
   
5. 
   Понятие о статически неопределимых балках
   

Балка — конструктивная деталь в виде прямого бруса, закрепленная на опорах и изгибаемая приложенными к ней силами. Высота сечения балки незначительна по сравнению с длиной.

Виды нагрузок на балку:



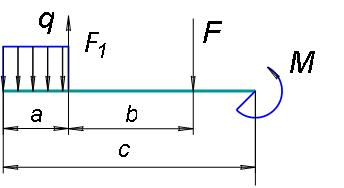
Рис 4.1
По способу приложения нагрузки делятся на сосредоточенные и распределенные. Если реально передача нагрузки происходит на пренебрежимо малой площадке (в точке) (рис. 4.1 сила F и F₁), нагрузку называют сосредоточенной.

Часто нагрузка распределена по значительной площадке или линии (давление воды на плотину, давление снега на крышу и т.п.), тогда нагрузку считают 

---

распределенной (рис. 4.1 нагрузка q).

В задачах статики для абсолютно твердых тел распределенную нагрузку можно заменить равнодействующей сосредоточенной силой (рис 4.2), равной по величине произведению распределенной нагрузке на длину нагруженного участка и приложенную посередине нагруженного участка.



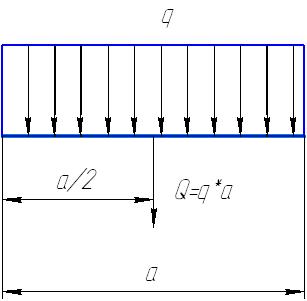
Рис. 4.2
На балку также может действовать пара сил (рис.4.1 изгибающий момент M).

Для передачи нагрузок балка должна быть зафиксирована относительно корпуса (фундамента, плиты и пр.). Фиксирование осуществляют с помощью опор — устройств (элементов конструкций), воспринимающих внешние силы. Конструкции опор разнообразны. Различают три основных типа опор.

Шарнирно-подвижная опора – опора, которая допускает поворот сечения балки над опорой и поступательное перемещение вдоль опорной поверхности. Схематическое изображе­ние такой опоры показано на рис. рис. 4.3, опорная реакция в этом случае направлена перпендикулярно, плоскости опирания катков.

 



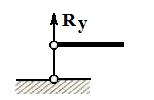
Рис. 4.3

 

Шарнирно-неподвижная опора – опора, допускающая только угловое смещение (поворот вокруг собственной оси) и не воспринимающая моментной нагрузки. Схематическое изображение опоры показано на рис. 4.4; реакция такой опоры разлагается на две взаимно ортогональные составляющие.



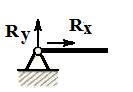
Рис. 4.4

 

Жесткая заделка (защемление) – опора, исключающая осевые и угловые смещения балки и воспринимающая осевые силы и моментную нагрузку. Схематическое изображение опоры показано на рис. 4.5. Реакция такой опоры имеет три составляющие – вертикальную, горизонтальную и реактивный момент.



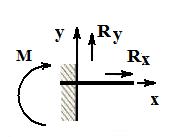
Рис. 4.5

 

Балки, имеющие две опоры, называют однопролетными, двухопорными или простыми. Балку, защемленную одним концом и не имеющую других опор, называют консольной балкой (консолью). Консолями называют также свешивающиеся за опоры части балки.

---

Под действием внешних нагрузок в местах закрепления стержня возникают опорные реакции. Так как деформации, изучаемые в сопротивлении материалов, малы по сравнению с размерами элементов конструкций, то при определении опорных реакций этими деформациями пренебрегают. Опорные реакции находят из уравнений статики. Балка будет находиться в равновесии, если суммы проекций на оси х и у (ось у перпендикулярна оси стержня) всех сил, приложенных к балке и сил реакций опор равны нулю, а также равна нулю сумма моментов всех сил относительно любой точки плоскости балки.

Пусть на балку (рис. 4.6), лежащую на опорах А и В действует вертикальная сосредоточенная сила F, распределенная нагрузка q, и момент M. На рисунке 4.7 приведены реакции опор системы, которые необходимо определить.



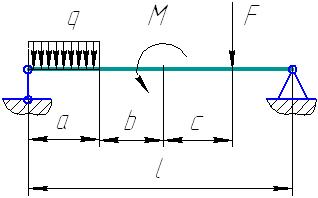
Рис. 4.6



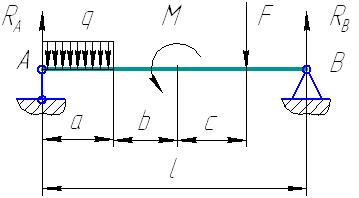
Рис. 4.7

Составим уравнения равновесия.




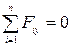
R_A-F –q*a+R_B = 0; (1)
 ,  (2)

 ,   (3)

 

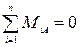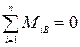Из уравнений (2) и (3) найдем силы реакций опор R_A и R_B. При подстановке значений R_A и R_B в выражение (1) данное равенство должно выполняться.

Пример решения задачи

Дана двухопорная балка, на которую действуют сила F = 50 кН, момент

М = 25 кНм, распределенная нагрузка q = 10кН/м, расстояние между опорами a= 6м, b= 5 м, с= 4м, l = 20 м.

Определить реакции опор в точках А и В.

Решение



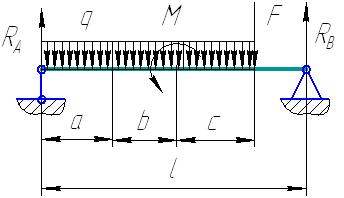
Составим уравнения равновесия с учетом реакций опор:

---

 , R_A - F – q * (a + b + c ) + R_B = 0; (1)

 ,   (2)

 ,   (3)

Из уравнения 2 определим R_B:

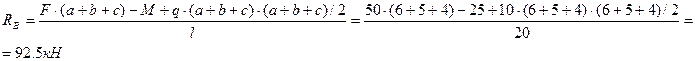 Из уравнения 3 определим R_A :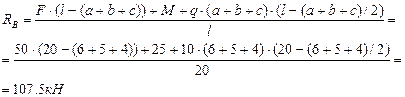



Проверка:

 , R_A - F – q * (a + b + c ) + R_B = 0

1072,5-50-10*(6+4+5)+92,5=0

0=0

Реакции найдены правильно.

Статически неопределимая (СН) балка

Статически неопределимыми называют балки, для которых при определении опорных реакций и внутренних силовых факторов недостаточно одних только уравнений равновесия.

Другими словами, СН балки имеют «лишние» опоры, которые дают дополнительные связи, сверх необходимых для удержания системы в равновесии.

Для раскрытия статической неопределимости таких балок требуются дополнительные уравнения, получаемые из условия отсутствия или совместности перемещений некоторых сечений.

СН балки – частный случай статически неопределимых систем.

Примеры статически неопределимых балок

Для удержания балки в геометрически неизменяемом, статичном положении (в равновесии) требуется одна заделка (рис. 4.8 а) либо две шарнирные опоры (рис. 4.8 б) одна из которых подвижная другая неподвижная.



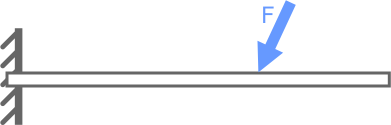
а



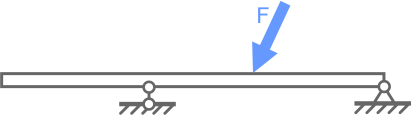
б

Рис. 4.8 Статически определимые балки

В этих случаях балка статически определима.
Добавление еще одной опоры (Рис. 4.9) упрочнит балку, но при этом она станет статически неопределимой.

---

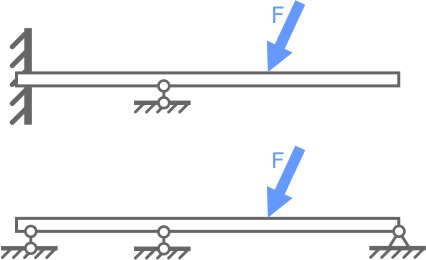
Рис. 4.9 Статически неопределимые балки

Усилия в дополнительных опорах являются лишними неизвестными при решении систем уравнений статики.

Степень статической неопределимости балки

Количество дополнительных связей показывает степень статической неопределимости балки, которую можно определить по формуле:

k=m-n

где m – общее количество неизвестных реакций связи балки, n – количество возможных уравнений равновесия которые можно составить для данной системы (для плоской – 3, пространственной – 6).

Балки с одной дополнительной связью называют однажды (один раз) неопределимыми, с двумя – дважды неопределимыми и т.д.

Раскрытие статической неопределимости

Расчет величины и направления лишних связей называют раскрытием статической неопределимости.

Так как для статически неопределимых балок возможных уравнений равновесия всегда меньше, чем неизвестных усилий для их расчета требуются дополнительные зависимости.

В качестве таковых используются условия отсутствия соответствующих линейных и/или угловых перемещений на опорах.

Существуют теоретические и практические методы раскрытия статической неопределимости.

Раскрыть статическую неопределимость балки можно с помощью метода начальных параметров или методом сил.

Практический метод определения лишней опорной реакции подробно рассмотрен здесь.

Контрольные вопросы:

1. 
   Дайте определение понятию «балка»?
   
2. 
   Какие бывают нагрузки по способу приложения?
   
3. 
   Что такое статически неопределимые балки?
   

---

Смотрите также файлы

• Отработка норматива гдзс 1.docx

• Презентация проекта представление учащимся проекта, выполненного им самостоятельно.docx

• ОбластиЯлуторовское межрайонное отделение судебных приставов Управления.pdf

• Самостоятельная работа к теме 4 Планирование и организация методического сопровождения педагогов в мкоу сош 7 с. Новомихайловка.docx

• Блім 3 блім Мдени мра.docx