Файл: Лабораторная работа 27 Наличие заготовки Присутствует 1 Отсутствует 0.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.01.2024
Просмотров: 26
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Оценочный лист
| № п/п | Материалы необходимые для оценки знаний, умений и навыков | Показатель оценивания | Критерии оценивания | Шкала оценивания | |
| 1 | Лабораторная работа № 27 | Наличие заготовки | Присутствует | 1 | |
| Отсутствует | 0 | ||||
| Правильность ответа на вопрос | Получены правильные ответы на вопросы | 3 | |||
| Получены частично правильные ответы | 1 | ||||
| Получены неправильные ответы | 0 | ||||
| Срок выполнения работы | Выполнение в срок | 2 | |||
| Выполнение с опозданием на 1 неделю и более | 0 | ||||
| Точность выводов | Выводы носят конкретный характер | 3 | |||
| Выводы носят формальный характер | 0 | ||||
| ИТОГО максимальное количество баллов | 10 | ||||
Цель работы - ознакомление с работой двоичных и недвоичных счетчиков. Исследование статических и динамических режимов счетчиков с последовательным и параллельным переносом, а также исследование распределителя импульсов на базе счетчика.
Исследование двоичных счетчиков в статическом и динамическом режимах
Счетчик с последовательным переносом
Таблица 1. Счетчик с последовательным переносом.
| n | Q4 | Q3 | Q2 | Q1 |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 2 | 0 | 0 | 1 | 0 |
| 3 | 0 | 0 | 1 | 1 |
| 4 | 0 | 1 | 0 | 0 |
| 5 | 0 | 1 | 0 | 1 |
| 6 | 0 | 1 | 1 | 0 |
| 7 | 0 | 1 | 1 | 1 |
| 8 | 1 | 0 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 |
| 10 | 1 | 0 | 1 | 0 |
| 11 | 1 | 0 | 1 | 1 |
| 12 | 1 | 1 | 0 | 0 |
| 13 | 1 | 1 | 0 | 1 |
| 14 | 1 | 1 | 1 | 0 |
| 15 | 1 | 1 | 1 | 1 |
| 16 | 0 | 0 | 0 | 0 |
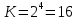

Рисунок 1. Счетчик с последовательным переносом.
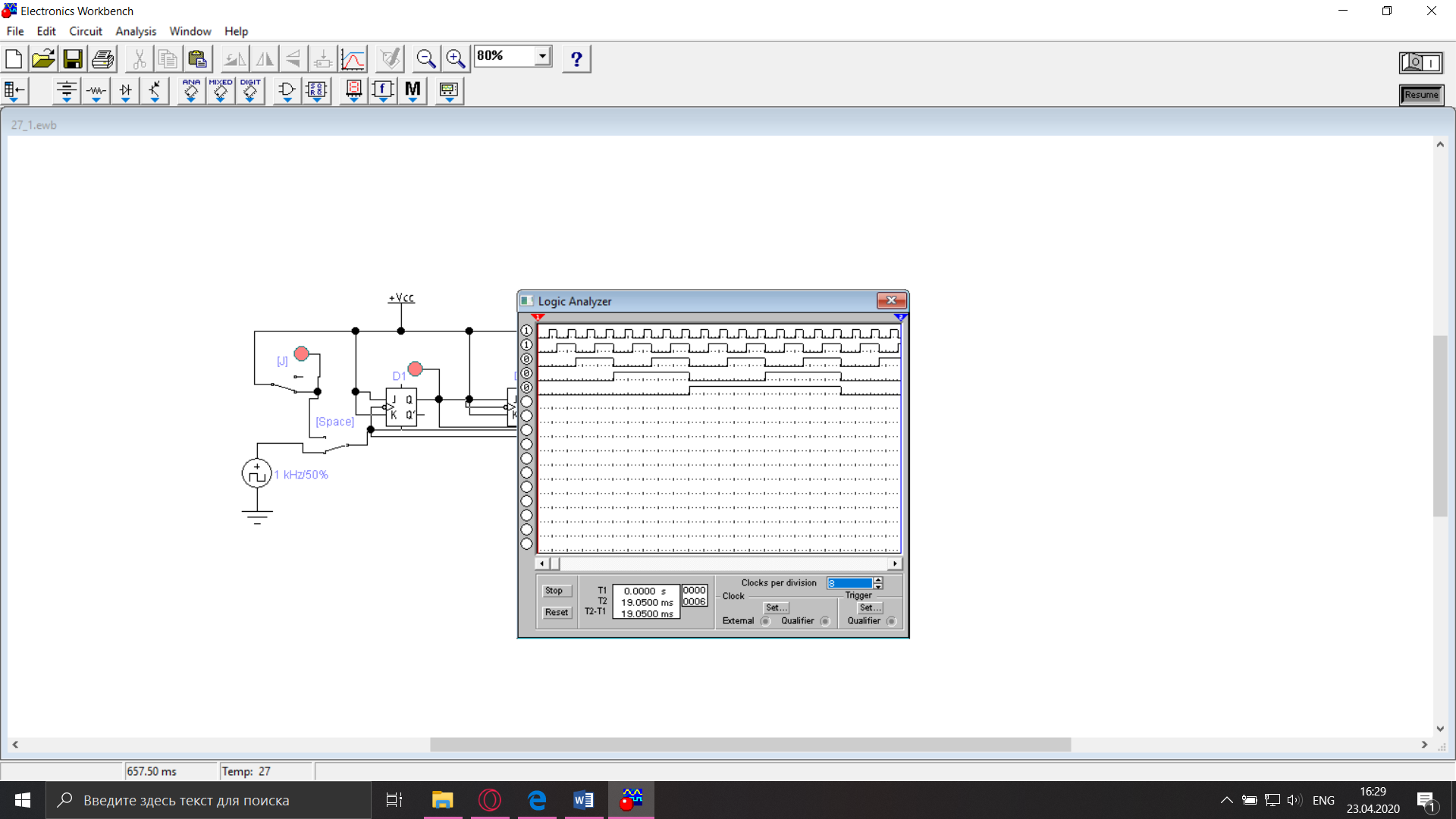
Рисунок 2. Диаграмма напряжений счетчика с последовательным переносом
Рисунок 3. Определение времени задержки
tзад.послед
 29 нс
29 нсСчетчик с параллельным переносом
Таблица 2. Счетчик с параллельным переносом.
| n | Q4 | Q3 | Q2 | Q1 |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 2 | 0 | 0 | 1 | 0 |
| 3 | 0 | 0 | 1 | 1 |
| 4 | 0 | 1 | 0 | 0 |
| 5 | 0 | 1 | 0 | 1 |
| 6 | 0 | 1 | 1 | 0 |
| 7 | 0 | 1 | 1 | 1 |
| 8 | 1 | 0 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 |
| 10 | 1 | 0 | 1 | 0 |
| 11 | 1 | 0 | 1 | 1 |
| 12 | 1 | 1 | 0 | 0 |
| 13 | 1 | 1 | 0 | 1 |
| 14 | 1 | 1 | 1 | 0 |
| 15 | 1 | 1 | 1 | 1 |
| 16 | 0 | 0 | 0 | 0 |

Рисунок 4. Счетчик с параллельным переносом.
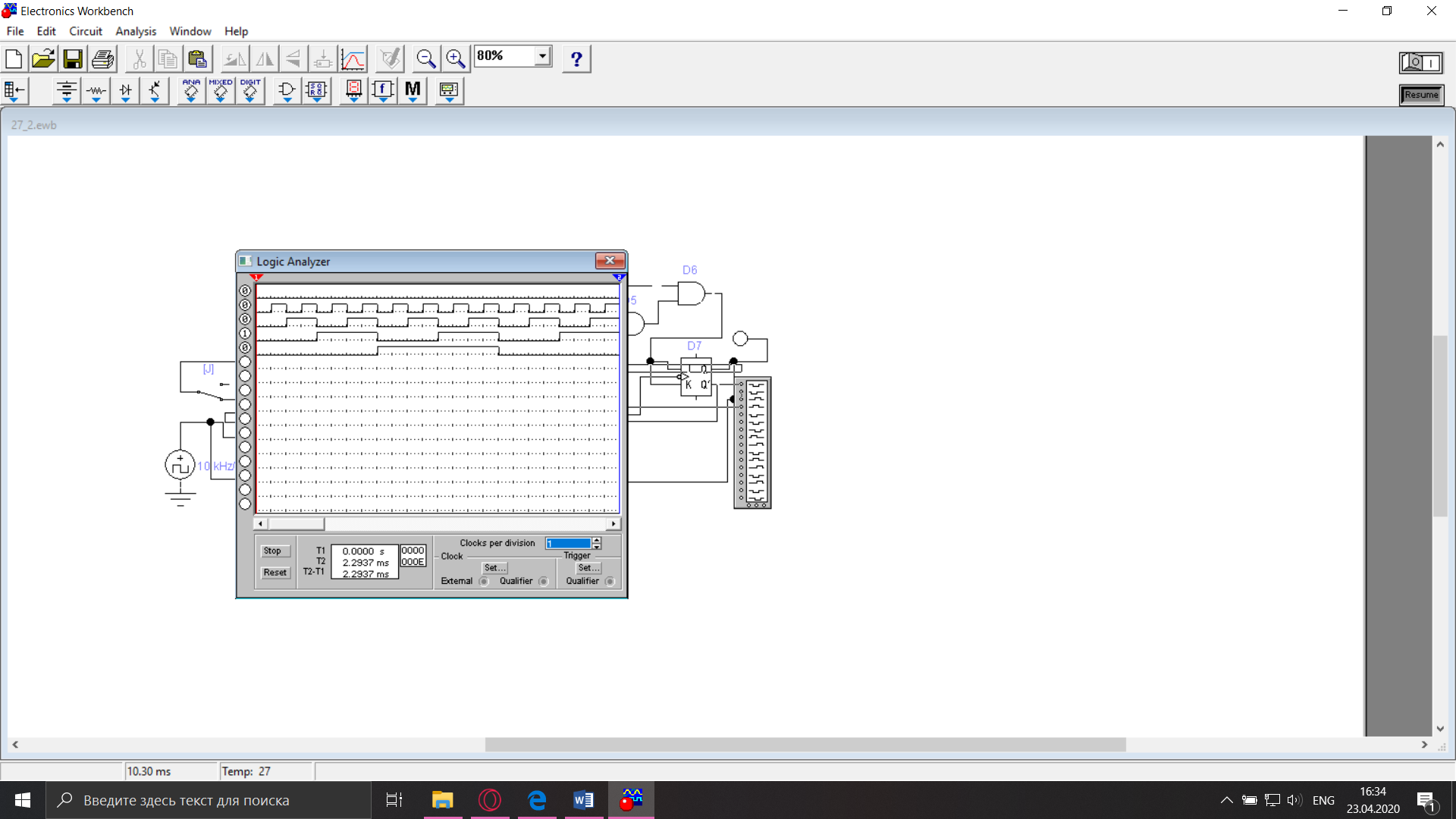
Рисунок 5. Диаграмма напряжений счетчика с параллельным переносом
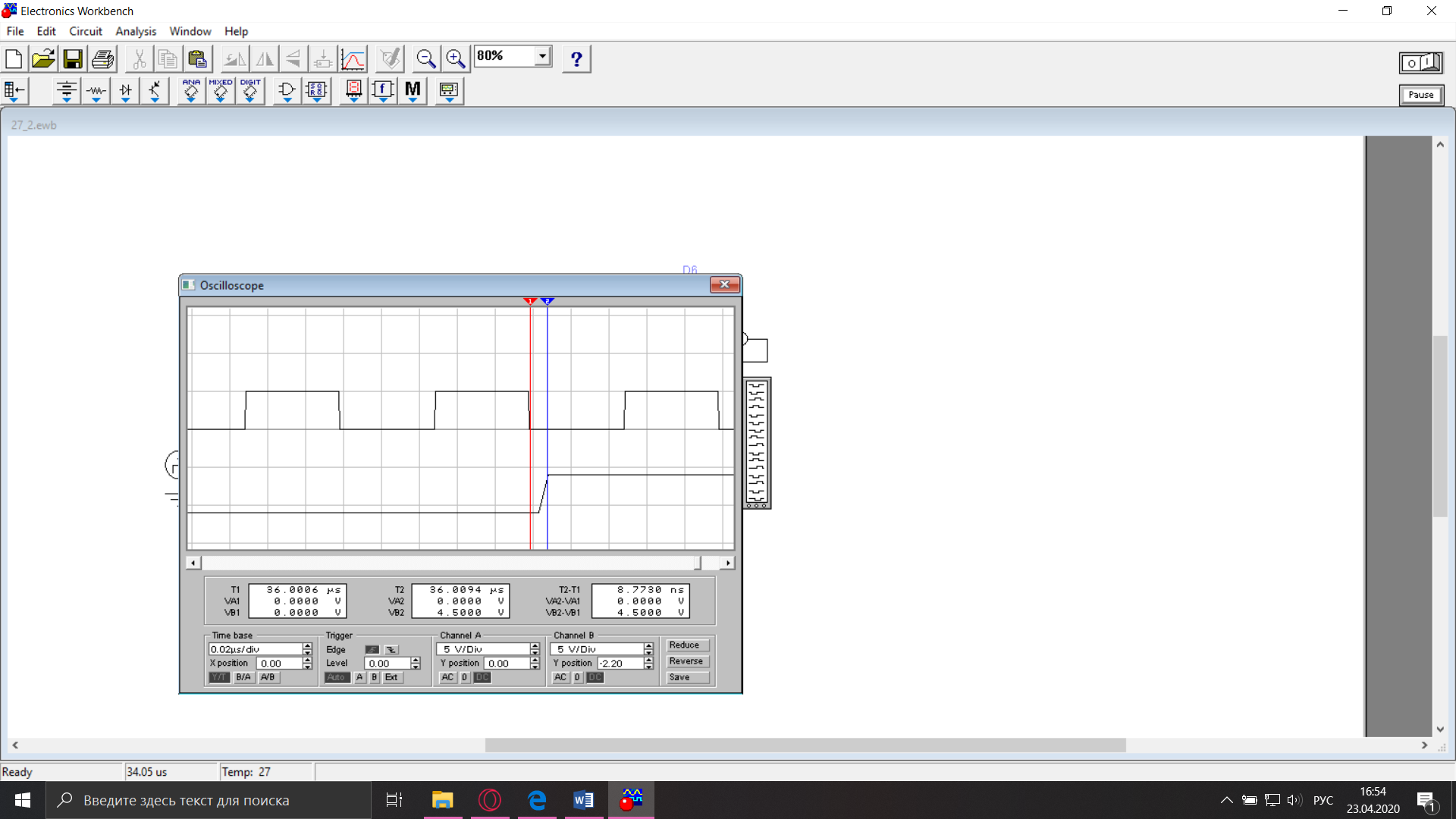
Рисунок 6. Определение времени задержки
tзад.парал
 9 нс
9 нсИсследование недвоичных счетчиков в статическом режиме
Таблица 3. Недвоичный счетчик с K = 9
| n | Q4 | Q3 | Q2 | Q1 |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 2 | 0 | 0 | 1 | 0 |
| 3 | 0 | 0 | 1 | 1 |
| 4 | 0 | 1 | 0 | 0 |
| 5 | 0 | 1 | 0 | 1 |
| 6 | 0 | 1 | 1 | 0 |
| 7 | 0 | 1 | 1 | 1 |
| 8 | 1 | 0 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 |
| 10 | 0 | 0 | 0 | 0 |
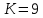
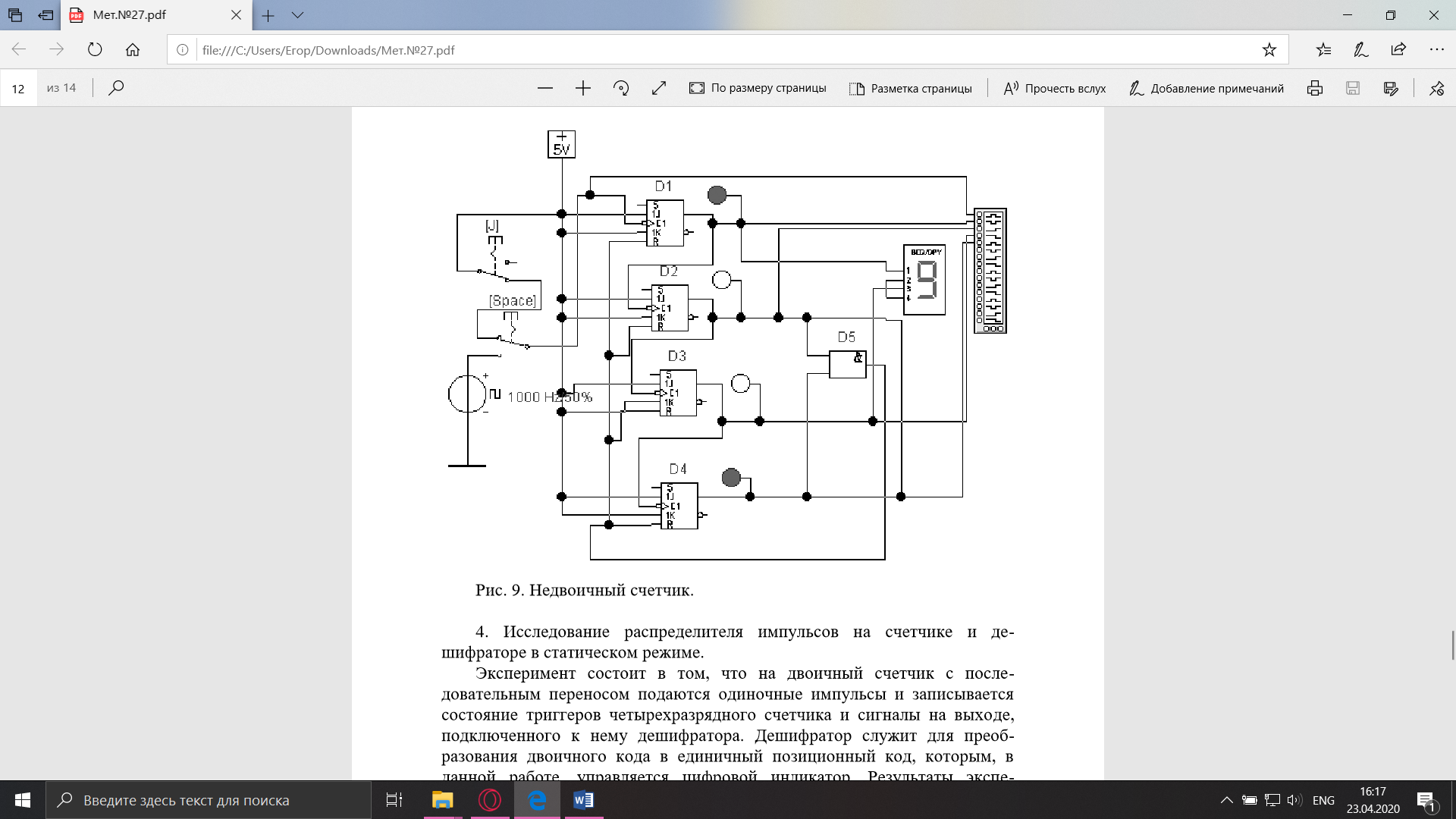
Рисунок 7. Недвоичный счетчик
Рисунок 8. Диаграмма напряжений недвоичного счетчика
Вывод.
В ходе работы были исследованы двоичные счетчики с последовательным и параллельным переносом в статическом и динамическом режиме работы.
Главное отличие счетчиков с последовательным переносом от счетчиков с параллельным переносом в том, что в триггеры в счетчике с последовательным переносом переключаются один за другим, что может привести к ложным комбинациям на выходе. Для того, устранения этого применяют счётчики с параллельным переносом. Принцип стробирования сводится к следующему: триггер меняет своё состояние при пропускании очередного импульса синхронизации, если все предыдущие триггеры находились в состоянии логической единицы. т.е. триггеры в счётчике с параллельным переносом переключаются практически одновременно в пределах разброса задержки входных элементов. Это преимущество счетчиков с параллельным переносом над счетчиками с последовательным переносом, хорошо видно из динамических характеристик и найденном времени задержки для каждого из видов счетчика.
Так же были исследованы недвоичные счетчики, сняты их статические и динамические характеристики. Можно создавать счетчики с произвольным коэффициентом пересчета, добавляя к выходу счётчика логику, которая будет определять нужную комбинацию на этих выходах и сбрасывать счётчик в 0. Например, так можно сделать двоично-десятичный счётчик из 4х Т триггеров и логического элемента И.