МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный электротехнический

Университет «ЛЭТИ» им. В.И.Ульянова (Ленина)
Кафедра МИТ

Индивидуальное Домашнее Задание

методические указания к решению задач на практических занятиях

по дисциплине: «Основы электроники и радиоматериалы»»

К.т.н. доцент Ситникова М.Ф.

Санкт-Петербург
2021

СОДЕРЖАНИЕ

Введение …………………………………………………………………………………………. 2

Индивидуальное домашнее задание……………………………………………………………. .2

Задание 1. Определить класс и формулу симметрии заданных материалов,

построить прямую и обратную элементарные ячейки заданных материалов ……………… .6

Задание 2. Построить элементарную ячейку Вигнера-Зейтца в обратном пространстве для заданных материалов. Определить размеры Зоны Бриллюэна в направлениях X, L, К. Указать индексы направлений X, L, К…………………………………………………………. 8

Задание 3. Определить симметрию кристаллической решетки в условиях

внешнего воздействия. …………………………………………………………………………10

Задание 4. Определить концентрацию электронов для заданного металла из условия касания зоны Бриллюэна и сферы Ферми и оценить возможность применения теории свободных электронов для заданного металла. ……………………………………………… .11

Задание 5. Определить эффективную массу носителей заряда, их концентрацию и степень вырождения электронно-дырочного газа в полупроводнике в диапазоне температур … …14

Задание 6. Рассчитать и построить зависимости времени релаксации, средней длины свободного пробега и электропроводности от температуры для заданного металла…… 17

Задание 7. Рассчитать и построить зависимость электропроводности от толщины металлической пленки при заданной температуре. ………………………………………… 23

Задание 8. Рассчитать и построить зависимости концентрации носителей заряда, времени релаксации и электропроводности от температуры для заданного полупроводника 25

Задание 9. Рассчитать зависимости энергии Ферми и термодинамической работы выхода для заданного полупроводника от температуры. Построить энергетические диаграммы контактной пары металл-полупроводник …… …………………. 25

---

Задание 10. Рассчитать концентрацию носителей заряда в заданном полупроводнике для создания омического контакта к металлу……………………………………………………. .29

Задание 11. Сделать выводы и дать рекомендации по применению исследуемого контакта металл-полупроводник………………………………………………………………………….30

Заключение…………………………………………………………………………………… .30

Список рекомендованной литературы…………………………………………………………31

Приложение………………………………………………………………………………………32

ВВЕДЕНИЕ

Набор заданий и методика решения задач для практических занятий по дисциплине: «Основы электроники и радиоматериалы» представляет собой результат многолетней работы автора, включая чтение лекций, проведение практических и лабораторных занятий по дициплинам «Физическим основам микро- и нано-электроники» и «Основы электроники и радиоматериалы».

Методические указания к практическим занятиям по курсу «Основы электроники и радиоматериалы» предназначены для подготовки бакалавров по направлениям: 210400.62 – Радиотехника, 210700.62 – Инфокоммуникационные технологии и системы связи, 211000.62 – Конструирование и технология электронных средств, 210601.65 - Радиоэлектронные системы и комплексы ФРТ, а также для подготовки бакалавров на Открытом факультете.

Задачей практических занятий является изучение законов квантовой механики и зонной теории твердого тела; физических представлений, определяющих свойства и строение радиоматериалов и лежащих в основе методов разработки элементной базы и технологических процессов микро- и наноэлектроники, а также приобретения навыков анализа физических задач, с последующим выбором рационального решения с целью более глубокого освоения теоретического лекционного материала, умения производить оценочные и инженерные расчеты физических явлений и свойств твердых тел, грамотно пользоваться справочной литературой.

В указания включены задачи, позволяющие наряду с достижением вышеуказанных академических целей проследить динамику взаимосвязи микроструктуры и проявляемых физических свойств основных материалов,

---

используемых в современной радиоаппаратуре, микроэлектронике и соответствующей технологии производства.

Практические занятия проводятся с использованием программ MCAD, адаптированных для решения предлагаемых задач и приведенных в приложении.


Индивидуальное домашнее задание

« Исследование контактных явлений в структуре металл-полупроводник»

Формулировка задания:

---

Для заданной пары металл-полупроводник оценить кинетические свойства заданных материалов, рассчитать и построить энергетическую диаграмму и вольт-амперную характеристику контакта в заданном диапазоне температур, дать рекомендации по применению исследуемого контакта.

Каждому студенту в начале семестра выдается Шифр варианта XYZ (приложение)

Например: для варианта (5 6 4) исходные данные берутся - вариант 5 из таблицы 1, вариант 6 из таблицы 2, вариант 4 из таблицы 3, таким образом для данного варианта (564) заданной парой металл-полупроводник является металл Cr и полупроводник n-InSb c концентрацией примесей 10¹⁶ см³

Рекомендуемый порядок выполнения:

1) Определить класс симметрии заданных материалов, построить прямую и обратную элементарные ячейки заданных материалов. Определить размеры Зоны Бриллюэна в направлениях X, L, К.

2) Определить концентрацию электронов для заданного металла из условия касания зоны Бриллюэна и сферы Ферми и сделать суждение о применимости теории свободных электронов.

3) Рассчитать и построить зависимости средней длины свободного пробега, времени релаксации и электропроводности от температуры для металла в диапазоне температур

(0,1- 10) ТD (Приложение MCAD №3). Оценить степень дефектности металла по заданной величине удельного сопротивления.

4) Рассчитать и построить зависимость электропроводности от толщины металлической пленки при заданной температуре. (Приложение MCAD №4)

5) Определить эффективную массу носителей заряда, их концентрацию и степень вырождения электронно-дырочного газа в примесном полупроводнике в данном диапазоне температур. (Приложение MCAD №2), рассчитать и построить зависимости концентрации, подвижности и электропроводности от температуры для заданного примесного полупроводника. (Приложение MCAD № 5)

6) Рассчитать зависимости энергии Ферми и термодинамической работы выхода для примесного полупроводника от температуры.

7) Построить энергетическую диаграмму заданной пары металл-полупроводник в выбранном масштабе для случаев: без смещения, при прямом и обратном смещениях.

Рассчитать и построить вольт-амперную характеристику контакта в данном диапазоне температур. (Приложение MCAD №6)

8) Рассчитать концентрацию носителей заряда в заданном полупроводнике для создания омического контакта к металлу.

9) Сделать выводы и дать рекомендации по применению исследуемого контакта металл-полупроводник

Рекомендуемый порядок выполнения заданий:

Задание 1. Определить класс и формулу симметрии заданных материалов, построить прямую и обратную элементарные ячейки заданных материалов.

Описание структуры радиоматериалов основано на идеях кристаллофизики. Задачи этой темы посвящены описанию структуры кристаллов, индицированию узлов, ребер и плоскостей, изучению симметричных свойств кристаллических структур. Основными методами изучения физических свойств кристаллов являются методы и принципы кристаллофизики. Рассмотрим примеры для различных кристаллических структур.

Пример 1.1. Написать формулу симметрии прямой тетрагональной призмы, являющейся одной из решеток Браве.

Для решения задачи необходимо воспользоваться основными положениями описания структуры кристалла.

Кристаллическая структура может быть, представлена в виде кристаллической (пространственной) решетки (КР), заполненной базисом (одним атомом или совокупностью атомов).

КР – математическая (геометрическая) абстракция, способ представления периодически повторяющихся в пространстве отдельных атомов (совокупности атомов).

Элементарная ячейка КР может быть построена на элементарных трансляциях (базисных векторах) a, b, c, так что все точки определяются радиус вектором:

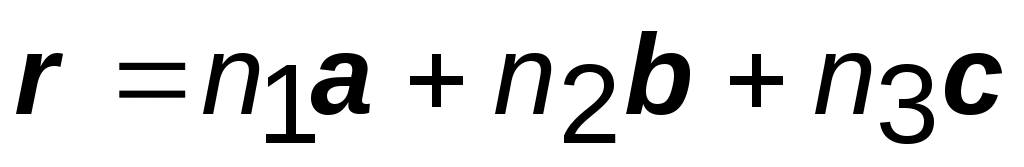, (1.1)

где – произвольные целые числа.

В зависимости от соотношения модулей базисных векторов, углов между ними и положения узлов, все элементарные ячейки можно классифицировать по Браве.

По соотношению между базисными векторами и углами, элементарные ячейки и соответствующие кристаллические многогранники подразделяются на три категории: высшую, среднюю и низшую, и 7сингоний.

Симметричные преобразования над кристаллическим многогранником образуют точечную группу и объединяются в класс симметрии.

Все элементы симметрии данного класса могут быть записаны формулой симметрии: например, для куба, имеющего 6 поворотных осей 2 порядка, 4 поворотные оси 3 порядка, 3 поворотных оси 4 порядка, 9 плоскостей симметрии и центр инверсии, формула симметрии: .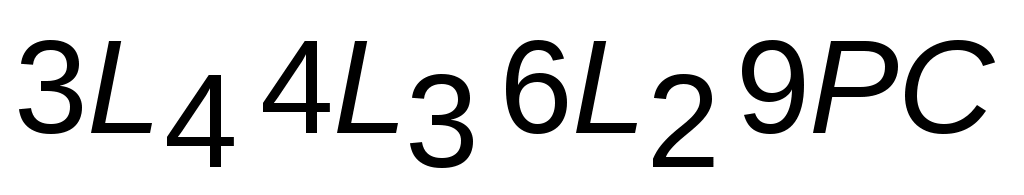

Рассматривая симметрию прямой тетрагональной призмы, выявляем (рис. 1.1) наличие осей 2, 3, 4, 6 порядка (возможных в твердом теле). В нашем случае есть четыре оси ось , нет осей 3 и 6 порядка.

Кроме того, у тетрагональной призмы есть горизонтальная плоскость симметрии P₁, два семейства вертикальных взаимно перпендикулярных плоскостей симметрии P₂, P₃ и P₄, P₅ и центр симметрии.


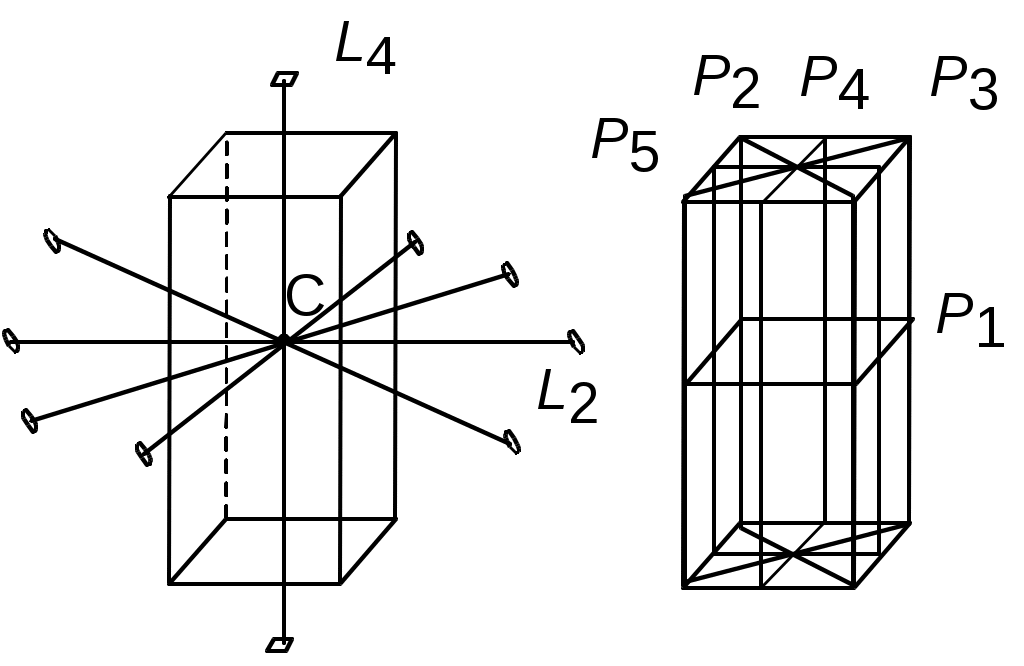
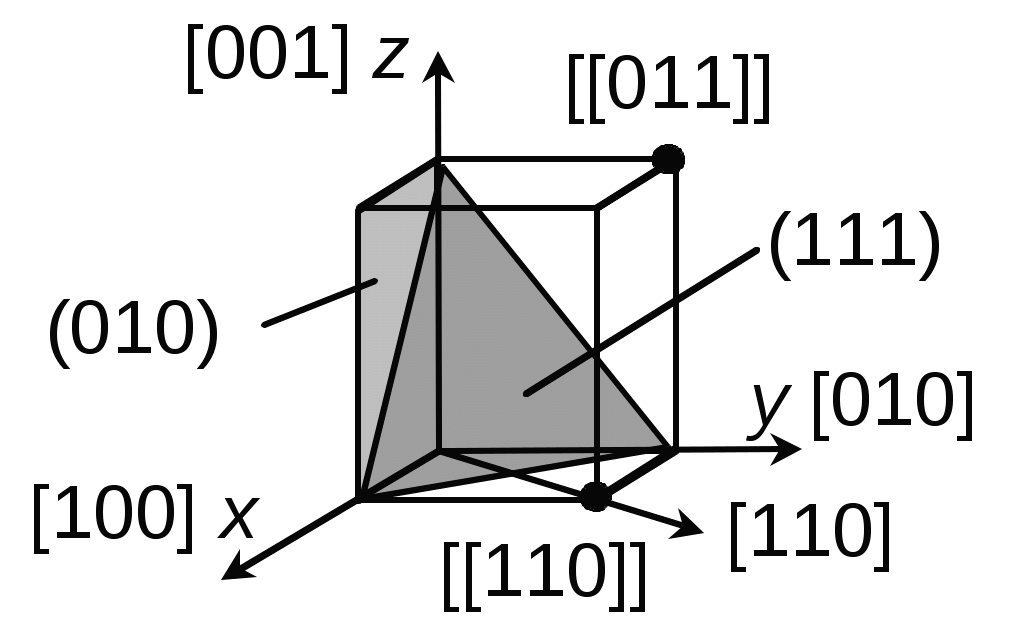
Рис. 1.1 Рис. 1.2
Пример 1.2. Найти векторы обратной решетки для ромбоэдрического кристалла кальция, если a = 5.36 Å, α = 46°.

Для описания свойств волнового вектора служит обратное пространство (или пространство волнового вектора). Связь обратного пространства (обратной решетки) с конфигурационным пространством (прямой решеткой) осуществляется соотношениями



(1.2)
где a*, b*, c*– базисные вектора обратной решетки, a, b, c– базисные вектора прямой решетки, V – объем элементарной ячейки.

В ромбоэдрической ячейке a = b = c, α = β = γ. Следовательно, согласно (1.2), a* = b* = c*, α* = β* = γ* (углы между базисными векторами обратной решетки).

Объем элементарной ячейки

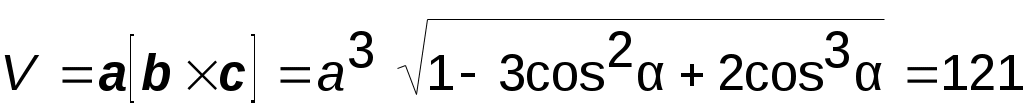(Å)³,

(Å)^–1,


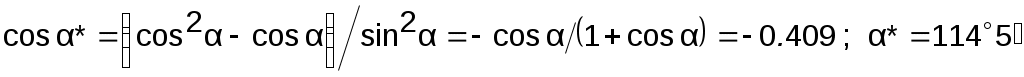
Пример 1.3. Определить базисные вектора прямой a_{i (}a₁,a₂,a₃) и обратной a*i

элементарных ячеек для ОЦК и ГЦК решеток.

Направляющие (базисные) вектора обратной решетки определяются выражениями 1.2


:

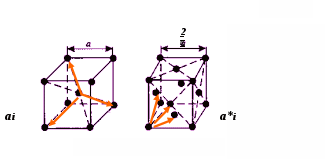
i=1,2,3
Рис. 1.3
Пример 1.4. Определить постоянную решетки кристалла NaCl, плотность кристалла ρ = 2.18·10³ кг/м³.

Плотность вещества зависит от типа структуры, плотности упаковки, атомной массы. С увеличением плотности упаковки возрастает и плотность вещества (кристалла). Плотность кристалла ρ связана с его относительной массой A, объемом элементарной ячейки V, числом атомов N в элементарной ячейке формулой (N_A – число Авогадро):

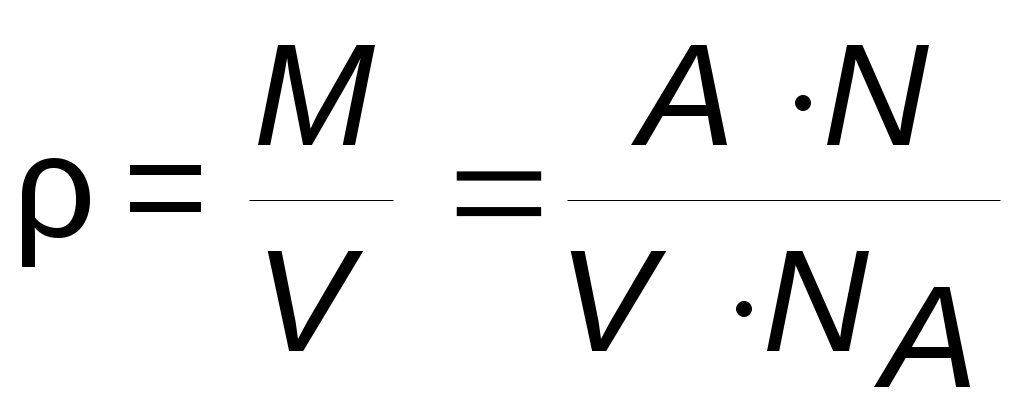. (1.3)

В кристалле NaCl можно выделить ячейку в виде куба, в вершинах которого поочередно находятся атомы Na и Cl. Ребро куба d, объем d³. Такая ячейка содержит 1/2 атома Na и 1/2 атома Cl. Если атомный вес , то масса выделенной ячейки из выражения (1.3):



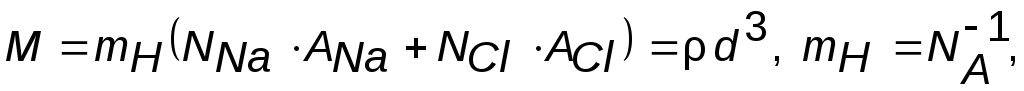
где 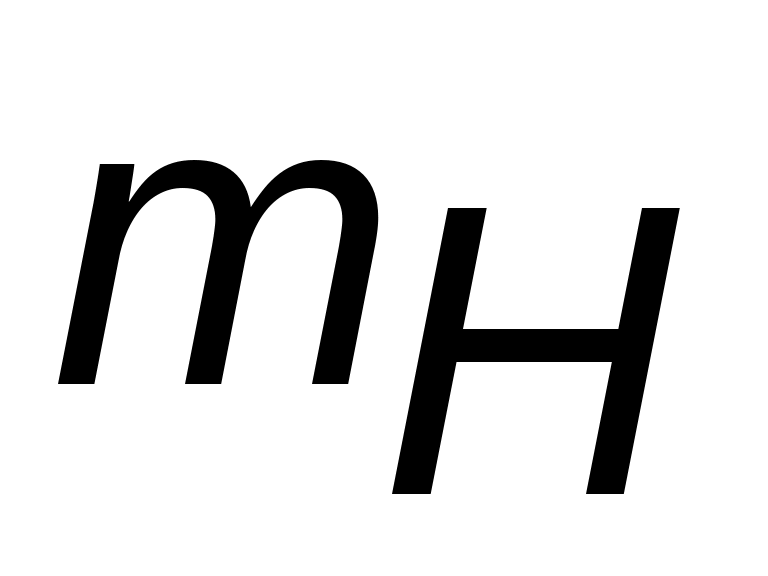– масса атома водорода, m_H= 1.66·10^–27кг, 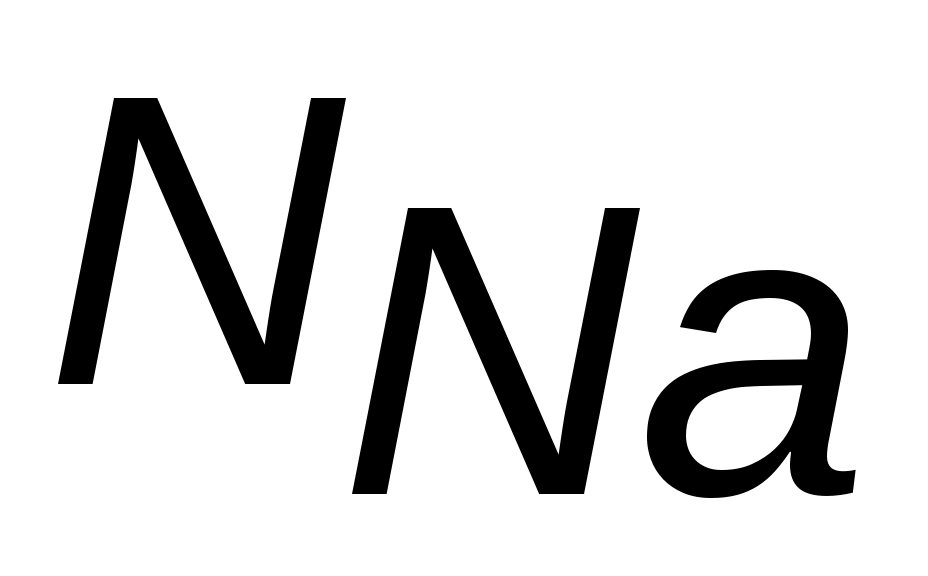и число атомов Na и Сl соответственно в выбранной ячейке. Разрешая формулу относительно d, получим:

.

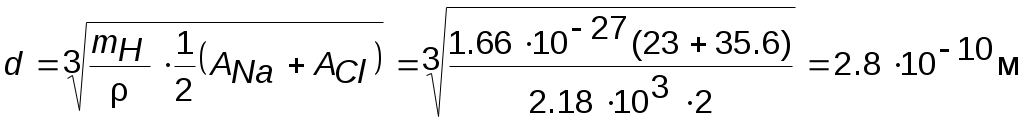Постоянная решетка кристалла определяется расстоянием между двумя одинаковыми атомами, т.е. a= 2d= 5.62Å.

Примечание. Применение соотношения (1.3) может быть полезным при оценке концентрации электронов n в кристаллах металлов по известной концентрации атомов N и валентности Z: n = NZ.

Задание 2. Построить элементарную ячейку Вигнера-Зейтца в обратном пространстве для заданных материалов. Определить размеры Зоны Бриллюэна в направлениях X, L, К. (рис.2.2) Указать индексы направлений X, L, К

Пример 2.1. Построить элементарную ячейку Вигнера-Зейтца для двумерной решетки

Построение ячейки Вигнера-Зейтца: 1. Выбирается узел решетки. 2. Проводятся линии, соединяющие этот узел с соседними узлами. 3. Через середины построенных линий проводятся плоскости, перпендикулярные к ним. Фигура, ограниченная этими плоскостями и есть ячейка Вигнера-Зейтца.(рис.2.1)



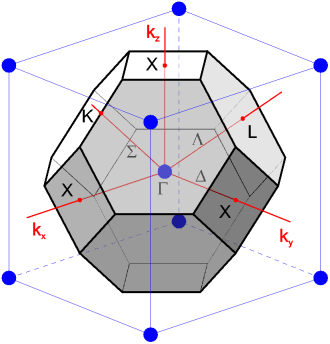
Рис. 2.1 Рис. 2.2

Построение 3-х мерной ячейки Вигнера проводится аналогично. Удобно это построение проследить на примере ГЦК решетки.

Как известно элементарная ячейка в обратном пространстве для ГЦК структур является объемноцентрированной. Выберем центральный узел в точке Г, соединим его с узлами в вершинах куба и через середины полученных отрезков перпендикулярно им проведем плоскости (111), и получим фигуру, называемую «усеченный кубооктаэдр», ограненный квадратными и шестиугольными плоскостями (рис.2.2). На этом же рисунке показаны характерные точки X, L,K, Σ, Δ, Λ, Γ.

Пример 2.2. Найти индексы плоскости, отсекающей по кристаллографическим осям отрезки 9, 10, 30, если базисные вектора ,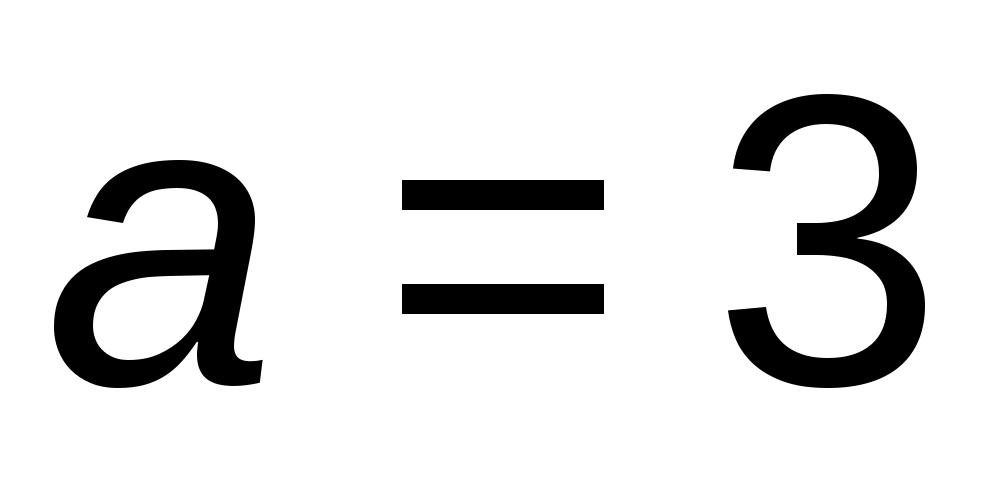

Для индицирования (описания) узлов, направлений и плоскостей в кристаллах используют индексы (рис. 1.2.).

Если r – радиус-вектор, проведенный из начала координат в рассматриваемый узел, то индексами узла будет совокупность чисел 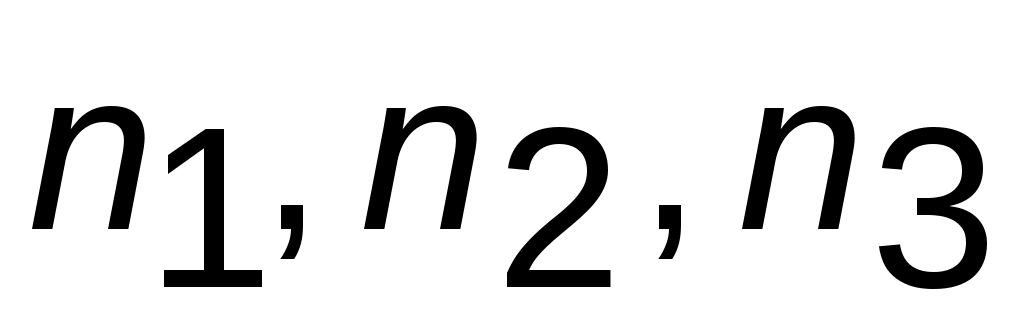в уравнении (1.1), записываемая .

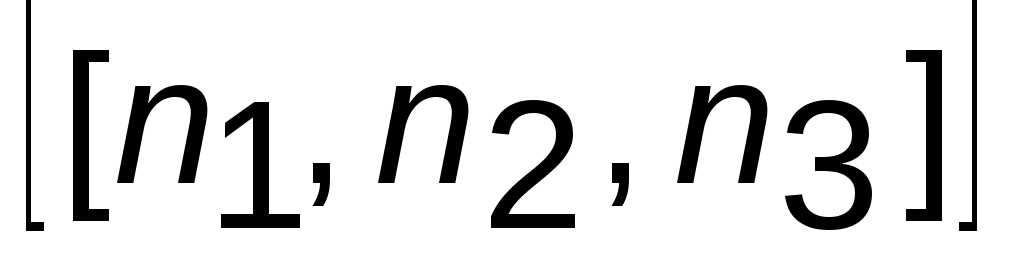За индексы направления ребра принимаются индексы ближайшего к началу координат узла, через которое проходит рассматриваемое направление, проведенное из начала координат .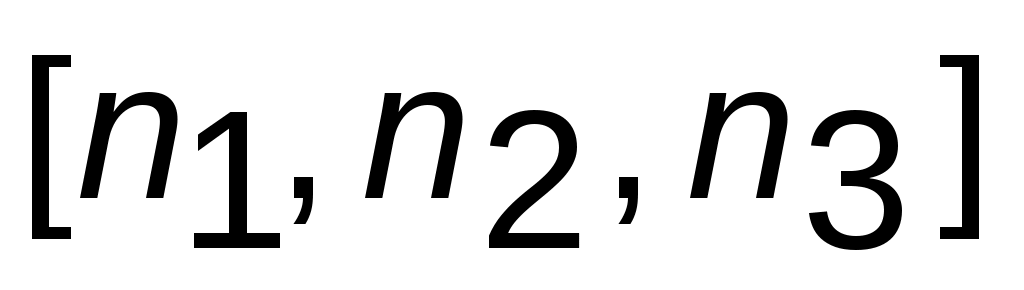

Индексы Миллера для плоскости представляют собой коэффициенты в уравнении плоскости, написанном в параметрическом виде; для нахождения индексов Миллера следует:

а) выразить отрезки, отсекаемые плоскостью на осях координат, через базисные отрезки (вектора)

б) найти обратные значения этих величин; привести их к виду наименьших возможных рациональных дробей, имеющих общий знаменатель;

в) отбросить общий знаменатель и заключить полученные три числа в круглые скобки .

В нашей задаче действуем, согласно указанному правилу:

а) выразим отрезки, отсекаемые плоскостью на осях координат, через базисные вектора:



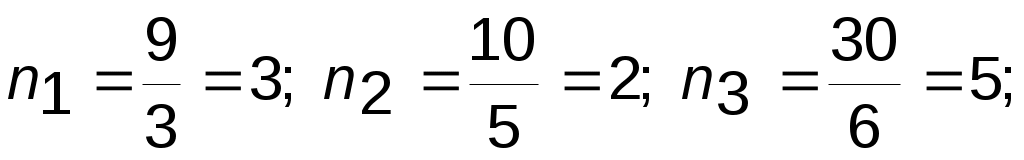
б) найдем обратные числа:



в) приведем их к наименьшему общему знаменателю:



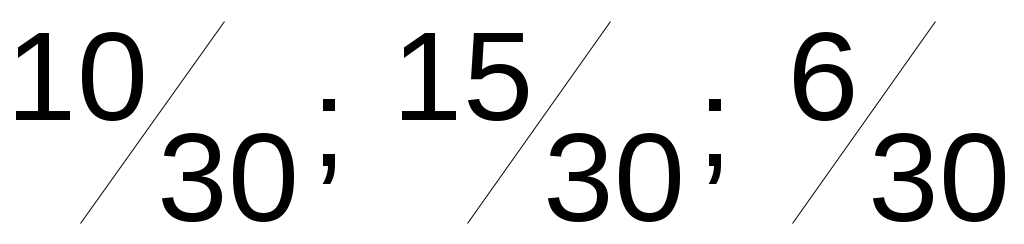
и отбросим знаменатель. Полученные числа есть индексы Миллера искомой плоскости (hkl) = (10,15,6).
Задание 3. Определить симметрию кристаллической решетки в условиях внешнего воздействия.

Пример 3.1. К кубическому кристаллу с симметрией приложили одноосное напряжение растяжения вдоль оси . Какой симметрией будет обладать кристалл?

Взаимосвязь физических свойств кристаллов и симметрии их структуры описывается принципами кристаллофизики.

Принцип Неймана:

Группа симметрии любого физического свойства кристалла должна включать в себя группу симметрии кристалла.

Для описания симметрии физических свойств и внешних воздействий служат предельные группы симметрии (группы Кюри), содержащие оси бесконечного порядка.

Принцип суперпозиции Кюри:

Кристалл, находящийся под влиянием внешнего воздействия, будет обладать теми элементами симметрии, которые являются общими для воздействия и кристалла в отсутствии воздействия. Свойства кристалла, связывающие воздействия явления, можно отобразить схемой:

(явление (эффект)) = (свойство) x (воздействие). (3.1)

По условию задачи, растягивающее напряжение приложено по оси вдоль направления [0 0 0]. Симметрия приложенного воздействия соответствует предельной группе с геометрическим образом в виде покоящегося цилиндра вращения.

Применяя принцип суперпозиции Кюри (3.1), найдем общие элементы для кристалла в отсутствии воздействия и воздействия в отсутствии кристалла (рис. 1.4).

Общими элементами симметрии будут ось , четыре вертикальные плоскости, проходящие параллельно , одна перпендикулярная оси горизонтальная плоскость, четыре оси на пересечении вертикальных плоскостей с горизонтальной плоскостью и центр инверсии.


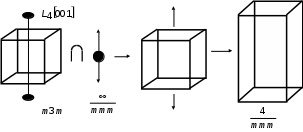
Рис. 3.1

Полученная симметрия соответствует симметрии тетрагональной призмы 4/mmm.

В аналитическом виде схеме (1.2) соответствует операция перемножения матрицы симметрии кристалла и матрицы предельной группы, соответствующей данному физическому воздействию, т.е.:



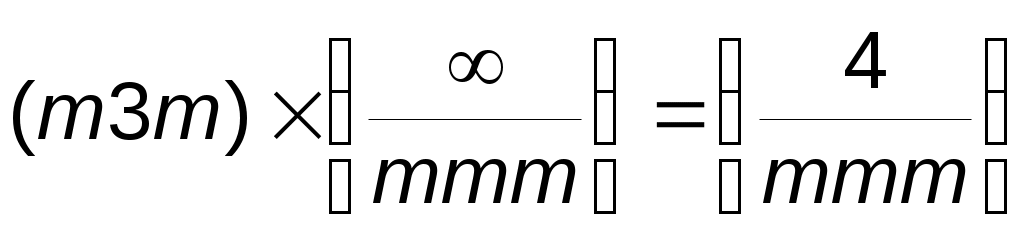
Задание 4. Определить концентрацию электронов для заданного металла из условия касания зоны Бриллюэна и сферы Ферми и оценить возможность применения теории свободных электронов для заданного металла.
Для описания поведения электронов в кристалле воспользуемся вероятностными законами квантовой механики и, так называемым, квазиклассическим приближением. Критерием выбора является соотношение между длиной волны де Бройля для частицы λ_Бр и характерным геометрическим размером системы, например, постоянной решетки a.

Соотношение де Бройля сопоставляет свободной частице с энергией E и импульсом p волну с частотой ω и длинной волны λ_Бр:

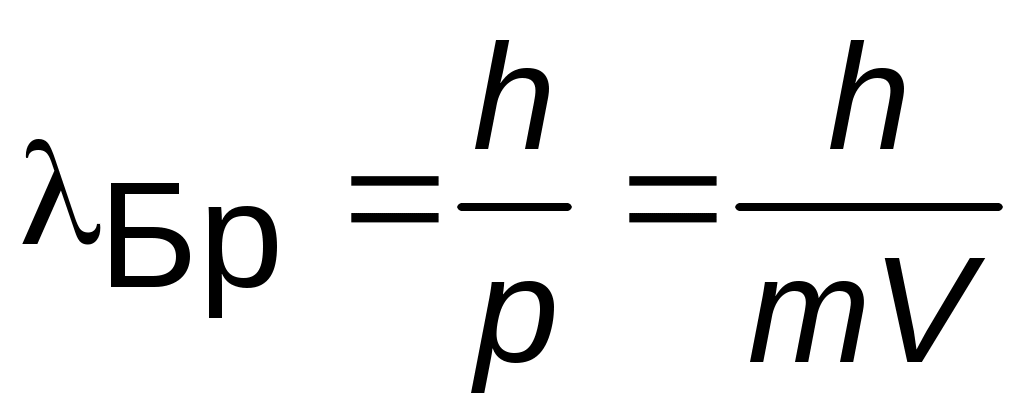. (4.1)

Если λ_Бр становится соизмеримой с a, частица описывается законами квантовой механики. В этом случае движение частицы определяется волновой функцией Ψ(r,t), которую находят из уравнения Шредингера

,

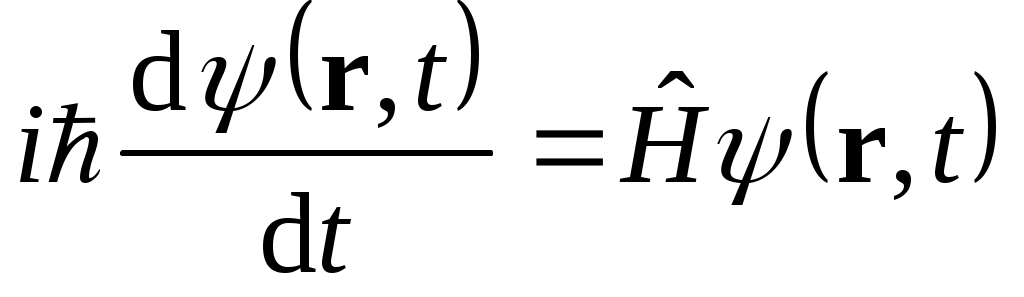где – оператор полной энергии.

Для характеристики частицы в пространстве необходимо решить стационарное уравнение Шредингера:

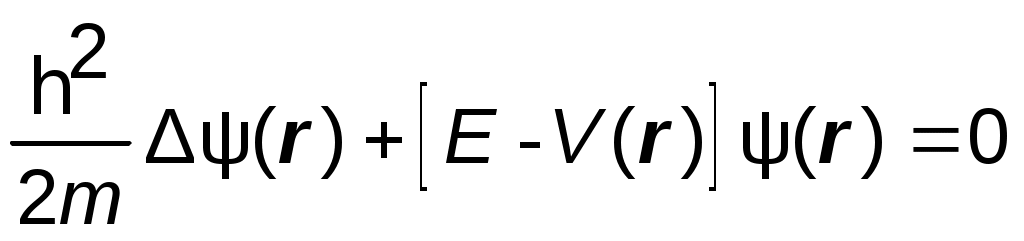(4.2)

и найти энергетический спектр, т.е. зависимость энергии частицы от волнового вектора k – волновой функции Ψ(r).

Пример 4.1. Найти длину волны де Бройля для электронов в электронном микроскопе с ускоряющим напряжением 50 В.

Для частицы в ускоряющем электрическом поле с потенциалом V соотношение (4.1) переходит в соотношение

.

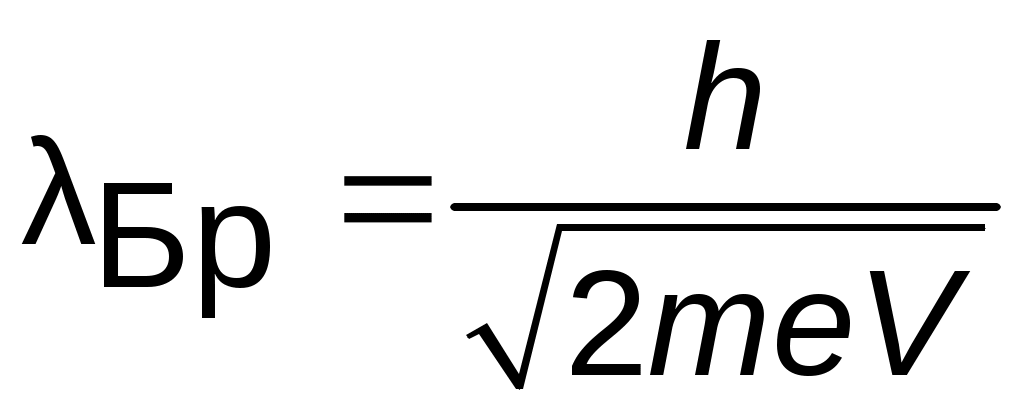Тогда для свободного электрона с массой m₀ и зарядом e имеем:



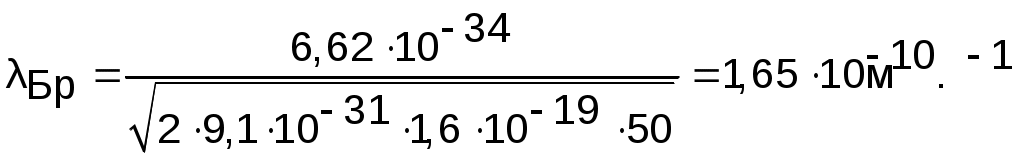
Пример 4.2. Найти энергетический спектр E(k) и волновую функцию Ψ_k(r) для свободных электронов.

Для свободной частицы V(r)=0 и уравнение Шредингера (4.2) имеет вид

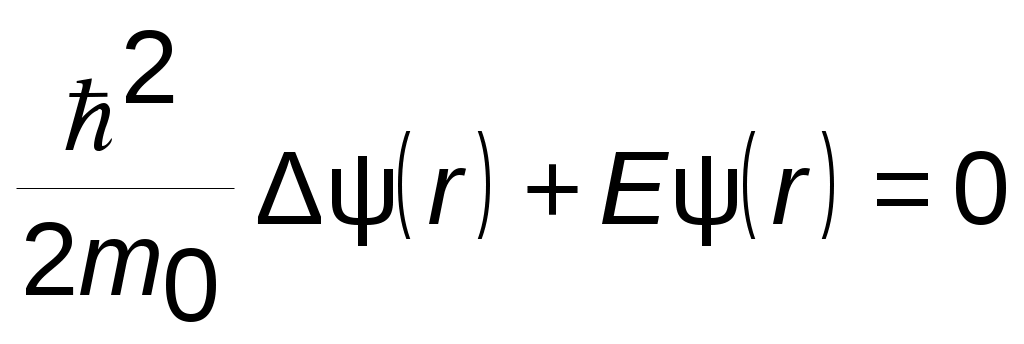. (4.3)

Решением уравнения (4.3) для свободных электронов является плоская волна де Бройля .

Энергия свободных электронов связана со значениями волнового вектора параболической зависимостью

.

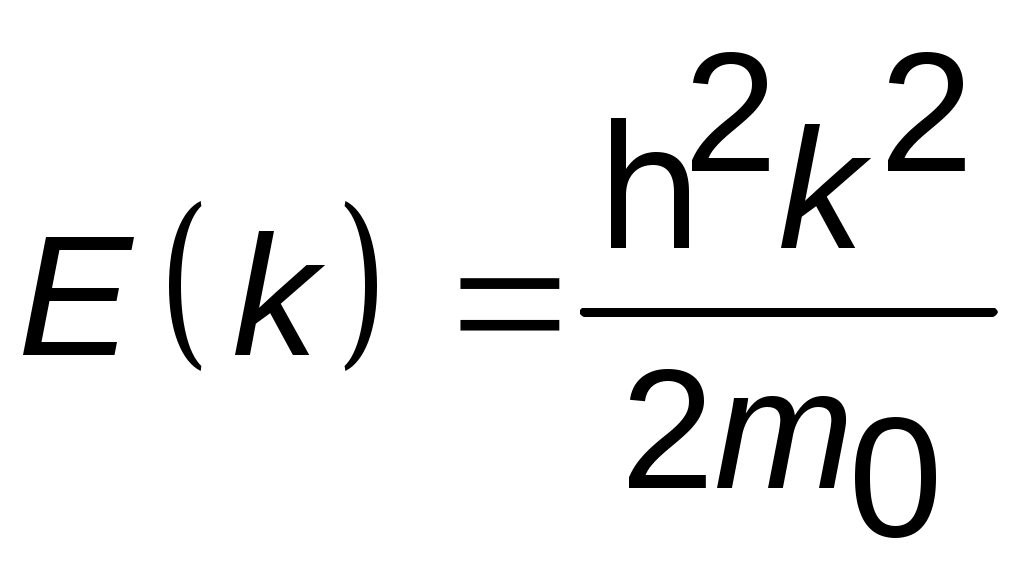Пример 4.3. Определить вид энергетического спектра для электронов в одномерной потенциальной яме с бесконечно высокими стенками и плоским дном. Найти энергию второго квантового состояния, если ширина ямы a = 5Ǻ, m = m₀.

Для частицы в одномерной потенциальной яме с бесконечно высокими стенками и плоским дном из решения (4.2) находим:



Для n= 2 получим

.

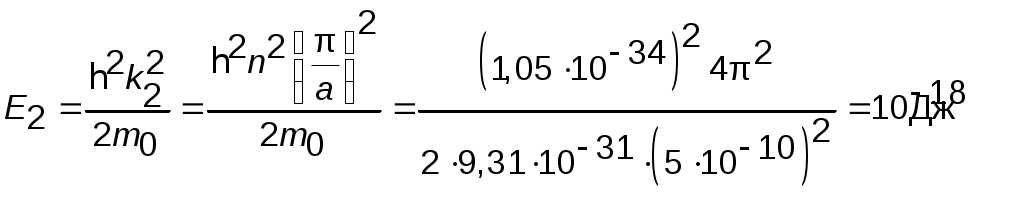Пример 4.4. В приближении слабой связи определить концентрацию электронов в кубических кристаллах из условия касания сферы Ферми и зоны Бриллюэна в обратном пространстве (a = 3Ǻ).

Потенциальное поле кристалла V(r) можно аппроксимировать повторяющимися с периодом a потенциальными барьерами заданной высоты. Решение уравнения Шредингера (4.2) в этом случае приводит к зависимости E(k) в виде повторяющихся разрешенных (РЗ) и запрещенных (33) зон значений энергии электронов (рис. 4.1).





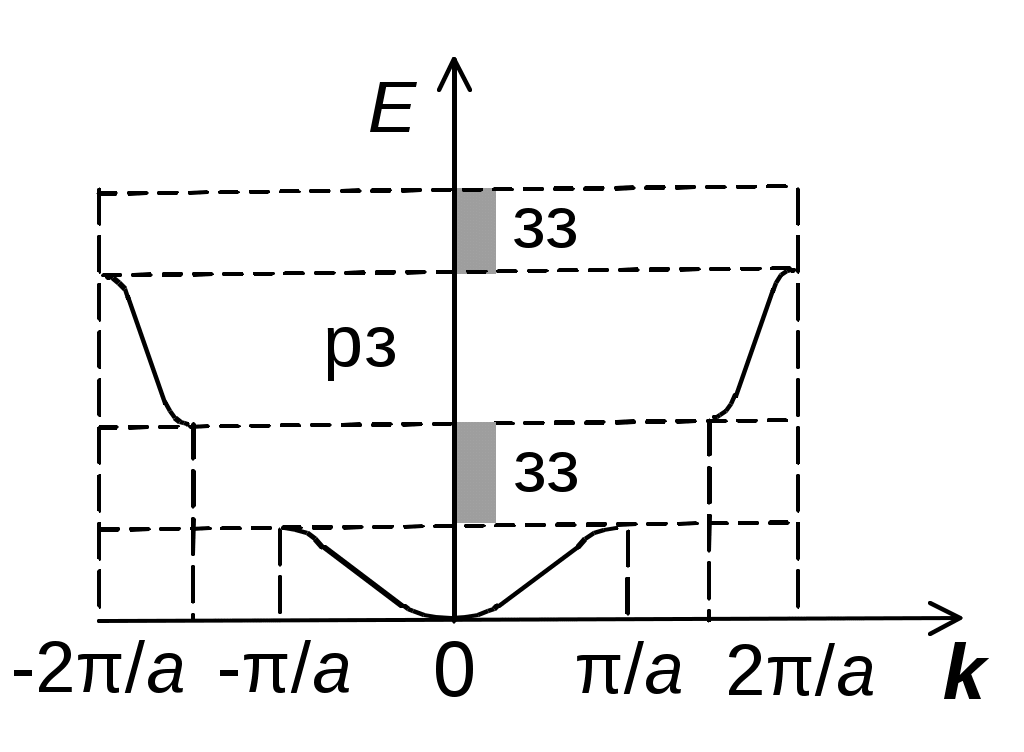
Рис 4.1 Рис 4.2

Функция E(k) имеет разрывы в точках (S=1,2,3…) и описывается выражением

.

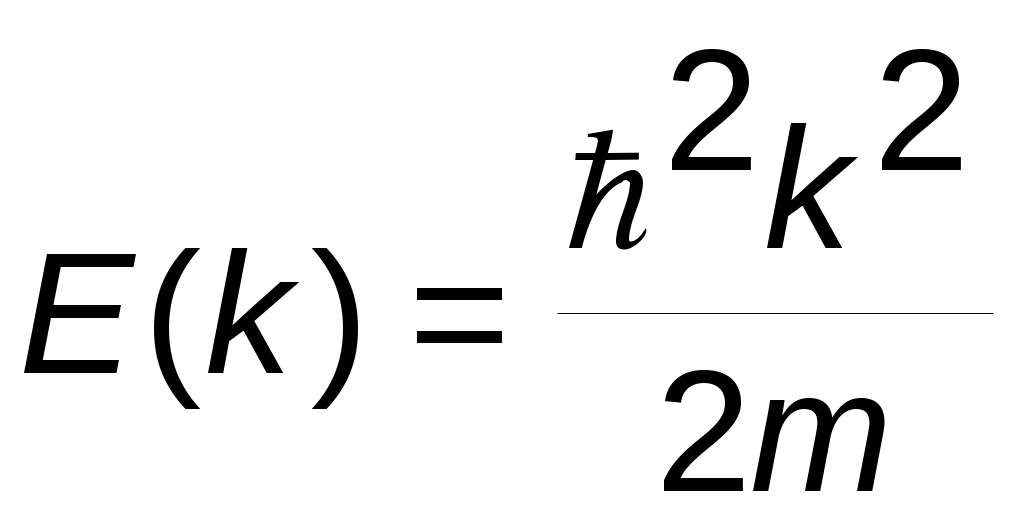Для изотропных кристаллов кубической сингонии зона Бриллюэна представляет собой куб со стороной 2π/a. Для 1 зоны Бриллюэна (s= 1)

k_Бр = ±π/a (рис. 4.2).

Для ГЦК, ОЦК и ГПУ структур выбираем наименьшее значение волнового вектора в направлениях к характерным точкам (границам зоны Бриллюэна) и сравниваем с радиусом поверхности Ферми.

Поверхность Ферми для слабо связанных (свободных) электронов есть сфера, радиус которой k_F связан с концентрацией электронов n зависимостью .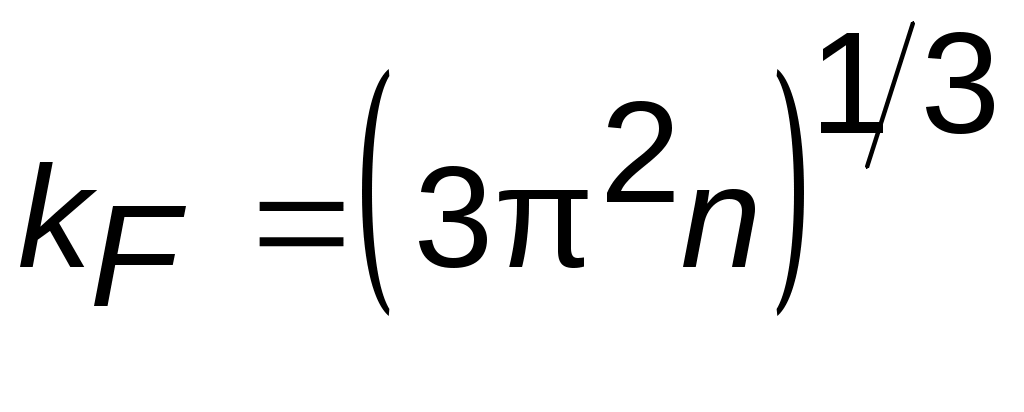

Из условия получаем .

Для заданного металла определяем концентрацию электронов по валентности Z, т. е. количества электронов, отдаваемых одним атомом в обобщенный электронный газ, и числом атомов N, приходящихся на одну элементарную ячейку объемом V: n₀=N*Z/V.

Если n₀ < n, то теория свободных электронов справедлива и применимо понятие Ферми-газа.


Задание 5. Определить эффективную массу носителей заряда, их концентрацию и степень вырождения электронно-дырочного газа в полупроводнике в данном диапазоне температур. (Приложение MCAD №2)

Для характеристики состояния большого числа частиц и квазичастиц в твердом теле, таких как электроны, фононы, дырки, атомы примеси и пр., используют классические и квантовые статистические распределения – статистику Больцмана для классических частиц, статистику Планка для фононов, статистику Ферми–Дирака для электронов и дырок в вырожденном состоянии.

Задачи этой темы способствуют формированию навыков правильного выбора и использования статистики для описания свойств частиц в заданных состояниях, главным образом электронов и дырок в металлах и полупроводниках. Для анализа состояния электронов и дырок студенты могут воспользоваться программой MCAD, приведенной в приложении П5.
Пример 5.1. Определить состояние электронного газа в кристалле кремния

(n = 10¹⁹ м^–3, m* = 0,7m₀) в диапазоне температур T = 77-300 K.

Состояние электронного газа в кристалле может быть вырожденным, т.е. описываться распределением Ферми–Дирака для системы квантовых частиц с полуцелым спином и химическим потенциалом, равным энергии Ферми :

, (5.1)

где – среднее число частиц в соответствии с энергией E_n при температуре T, – функция распределения частиц по состояниям с энергией .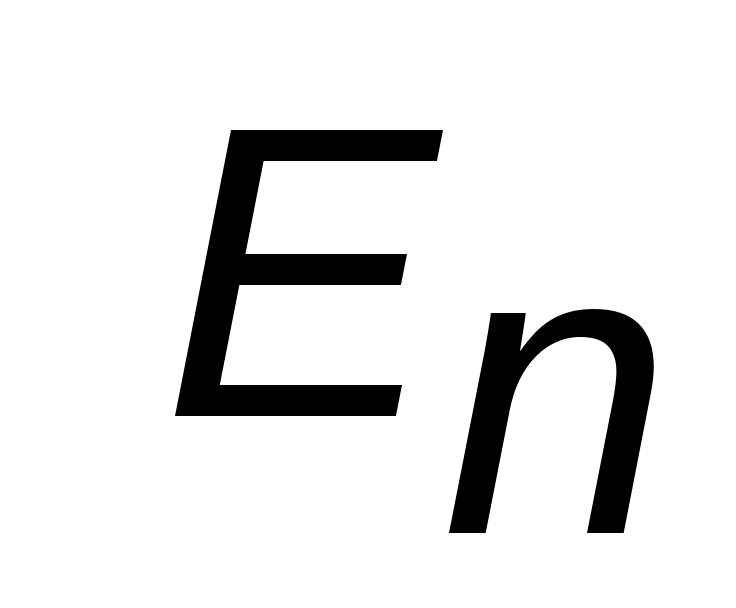

Если 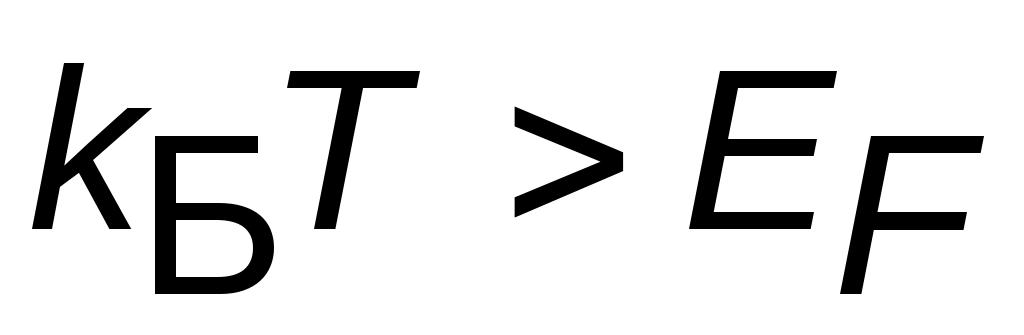для любого 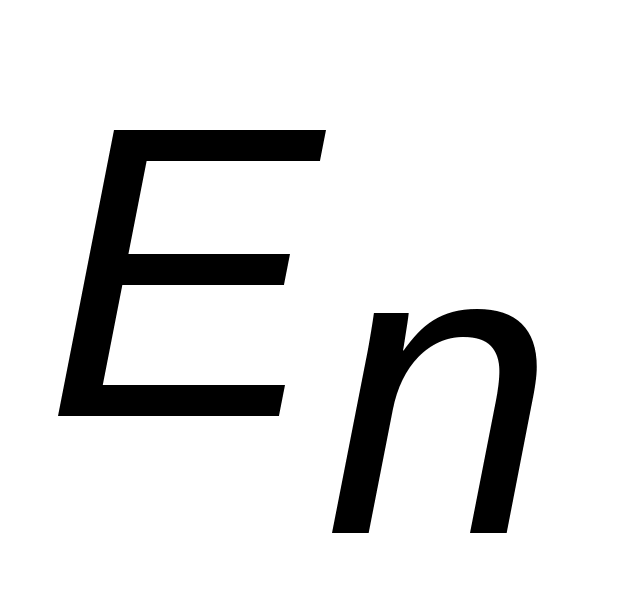, то (5.1) переходит в распределение для идеального газа электронов (дырок), которое называется невырожденным, и описывается распределением Больцмана по состояниям с энергией 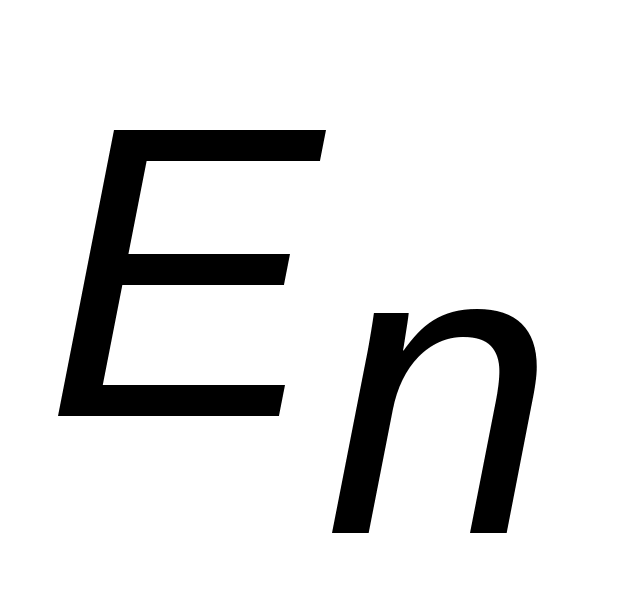для системы классических невзаимодействующих частиц:

,

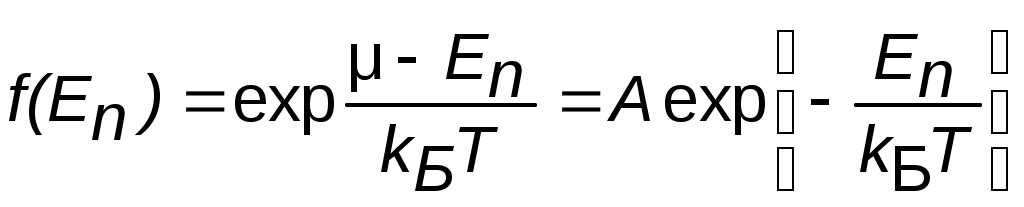где 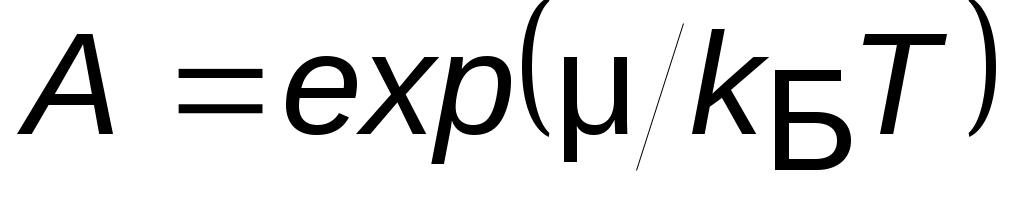, μ – химический потенциал.

Вырожденный электронный газ характеризуется значением параметров Ферми и прежде всего значением энергии Ферми E_F.

Изоэнергетическая поверхность в k – пространстве с энергией E= E_F называется поверхностью Ферми. Для свободного электронного газа с концентрацией электронов n и эффективной массой m* поверхность Ферми – сфера с радиусом k_F, при этом

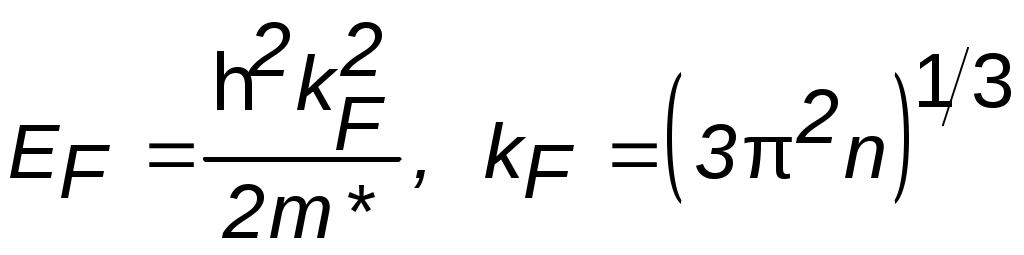. (5.2)

Для оценки степени вырождения электронного газа вычисляем энергию Ферми (5.2):



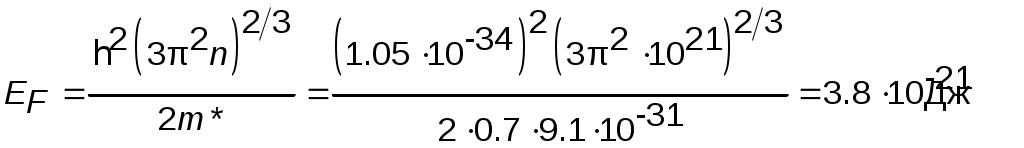
и тепловую энергию в заданном диапазоне температур E_Т:

при Т=77К , E_Т = k_БТ = 1.38∙10^–23∙77 = 1.06∙10^–21Дж < 3.8∙10^–21 Дж,

при Т=300К, E_Т = k_БТ = 1.38∙10^–23∙300 = 4.14∙10^–21Дж>3.8∙10^–21 Дж.
Используя критерий вырождения, в нашем случае для заданной концентрации электронов при Т = 77К имеем слабо вырожденный электронный (дырочный) газ, который при повышении температуры до 300К становится вырожденным и описывается распределением Ферми–Дирака (5.1),
Задание 6. Рассчитать и построить зависимости времени релаксации, средней длины свободного пробега и электропроводности от температуры для заданных материалов. (Приложение MCAD №3, № 5)

Для качественного описания кинетических явлений используют элементарный кинетический метод, в котором носители электрического заряда электроны (дырки) и носители тепла фононы рассматриваются как свободные частицы, при этом расчет ведется по отношению к одной частице, движущейся свободно между двумя последовательными столкновениями с различными рассеивающими центрами, с последующими усреднением по всем частицам. Согласно этой теории с учетом квантовых представлений, определяющих эффективную массу носителя заряда m", для электропроводности твердых тел пользуются выражением:

, (6.1)

где: n₀ - концентрации электронов, τ- время свободного пробега электрона (время релаксации).

Электропроводность материала может быть вычислена также по формуле

σ = enμ ,

где использовано соотношение между средним временем свободного пробега τ и подвижностью носителей заряда μ, μ=e/m*∙τ. Подвижность носителя заряда μ численно равна скорости дрейфа V_др в электрическом поле единичной напряженности ε.

Для решения задач этой темы студенты могут воспользоваться программами MCAD, приведенными в приложениях П6, П7 и П8.
Пример 6.1. Рассчитать удельное сопротивление и теплопроводность алюминия в диапазоне температур T = 77 - 400К, если измеренное удельное сопротивление образца при Т=0°С составляет 2,45 мкОм см и концентрация электронов n₀=10²⁹м^-3.

Для Al из П.1. находим a = 4.05Ǻ, T_D = 394K, T_пл = 933K.

Процессы рассеяния электронов в твердом теле можно подразделить на несколько видов, из которых в данной задаче будем рассматривать два: рассеяние электронов на фононах (тепловых колебаниях решетки) и рассеяние электронов на дефектах структуры.

Рассеяние электронов на фононах по-разному зависит от температуры.

Общее выражение для электропроводности, справедливое во всем температурном диапазоне, дается следующими соотношениями Блоха-Грюнайзена:

,

,

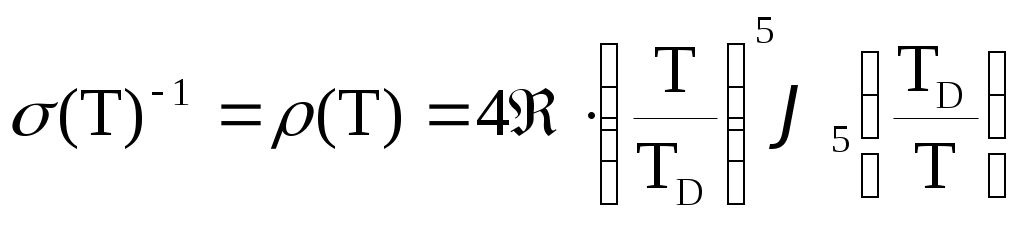где - приведенное идеальное сопротивление, z =hω/2πkT, x = T_D /T.

Приведенные соотношения позволяют определить электропроводность металла в двух предельных случаях: T >> T_D и T << T_D, используемых на практике для расчета.

При высоких температурах T >> T_D (температура Дебая) процесс рассеяния носит упругий характер, и средняя длина свободного пробега λ(T) определяется простой приближенной формулой:

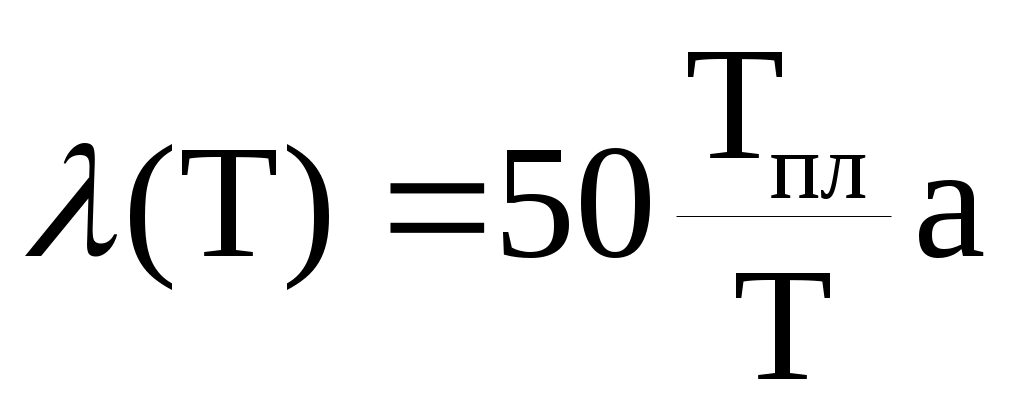, (6.2)

где: T_пл - температура плавления, a - параметр решетки материала.

При T << T_D характер рассеяния становится неупругим и λ(T) имеет вид:

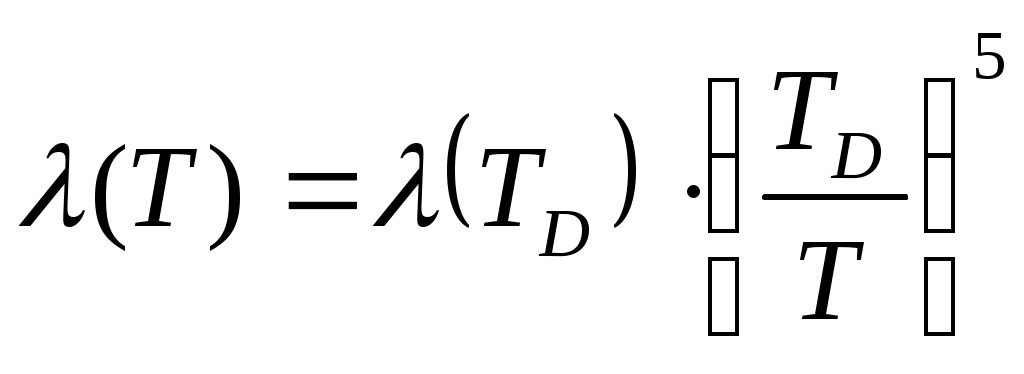. (6.3)

Соотношения (6.2), (6.3) позволяют приближенно оценить длину свободного пробега, определяемую рассеянием электронов на тепловых колебаниях решетки (фононах). На рис. 6.1 представлены зависимости λ₁(T) и λ₂(T), рассчитанные по формулам (6.2) и (6.3) соответственно для Al. Синим цветом выделена результирующая зависимость λ(T).


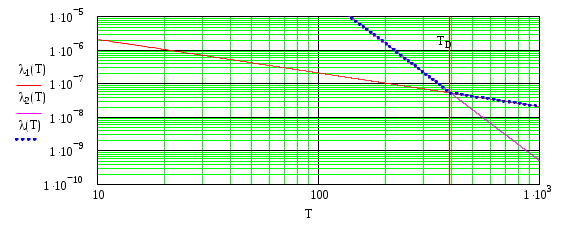
Рис.6.1

Время свободного пробега электронов в чистом металле τ_f(T):

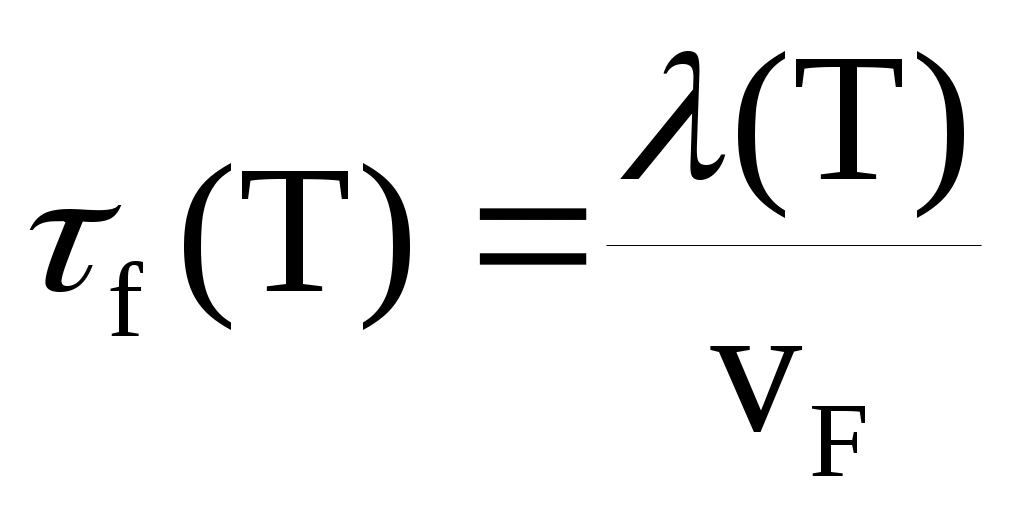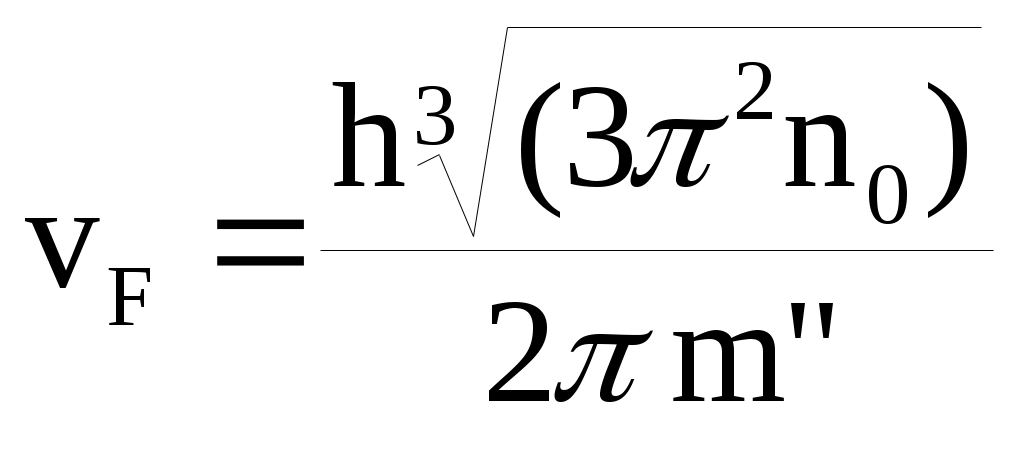, , (6.4)

где - скорость Ферми, h - постоянная Планка.

Время релаксации при рассеянии электронов на дефектах структуры в металле τ_d не зависит от температуры. Результирующее время релаксации τ_Σ при учете обоих механизмов рассеяния определяется правилом Маттиссена

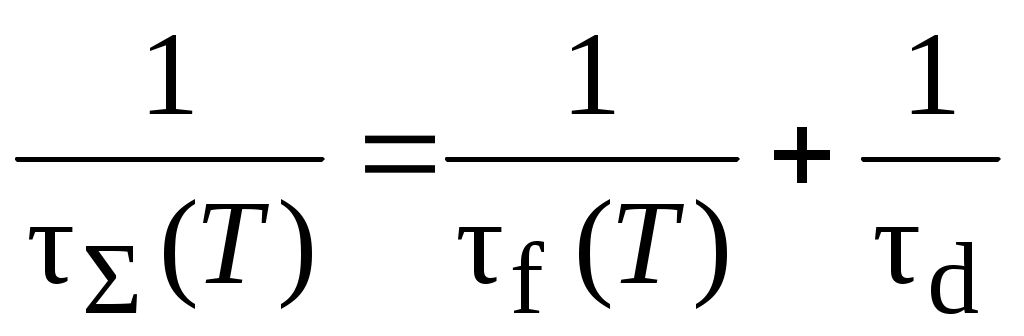, (6.5)

Формула 6.5 представляет собой алгебраическую сумму при условии преобладания одного из механизмов рассеяния.

Чтобы оценить вклад в электропроводность, вносимый рассеянием на дефектах структуры, сравним время свободного пробега электронов в чистом металле и для заданной задачи при 273К с результирующим временем релаксации τ_Σ(273). Из рис. 6.1 находим λ(273) =10^-7м, а согласно (6.4) получаем для скорости Ферми v_F= 2,1*10⁶м/c и времени свободного пробега электронов в чистом металле τ_f(273) =5* 10^-14 с. Используя выражение (5.1), по заданному измеренному значению удельного сопротивления образца при Т=0°С равному ρ=2,45 мкОм см находим результирующее время релаксации при учете обоих механизмов рассеяния: τ_Σ(273)10

---

^-15 с.

Сравнение показывает, что преобладающим является процесс рассеяния на дефектах структуры, т.к. он имеет меньшее значение на порядок (10^-15< 10^-14).

Теплопроводность κ(T) металла может быть определена на основе закона Видемана-Франца, который справедлив при высоких температурах (T >> T_D), а также при температурах столь низких, что рассеяние стационарными дефектами становится преобладающим:

, , (6.7)

где L₀ - число Лоренца. На рис. 6.2 и 6.3 представлены зависимости σ(T) и k(T) для металла различной степени очистки (стрелкой обозначен сдвиг кривых при увеличении концентрации дефектов в металле).



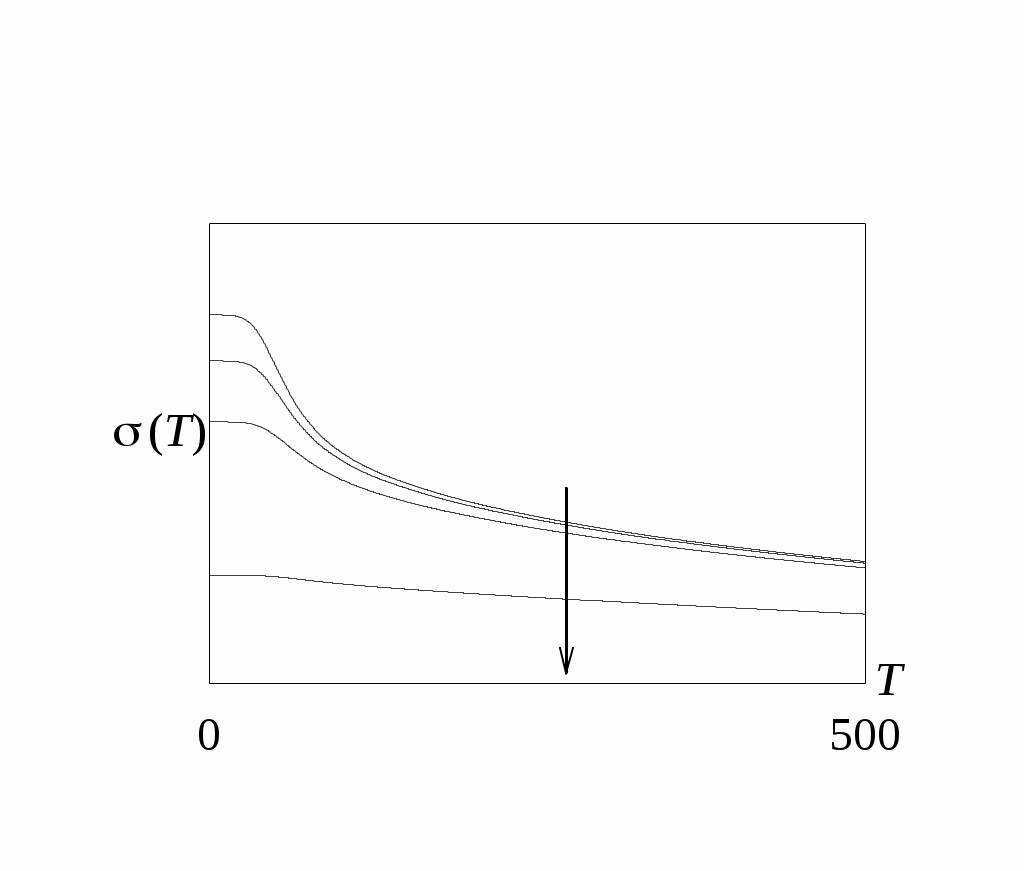
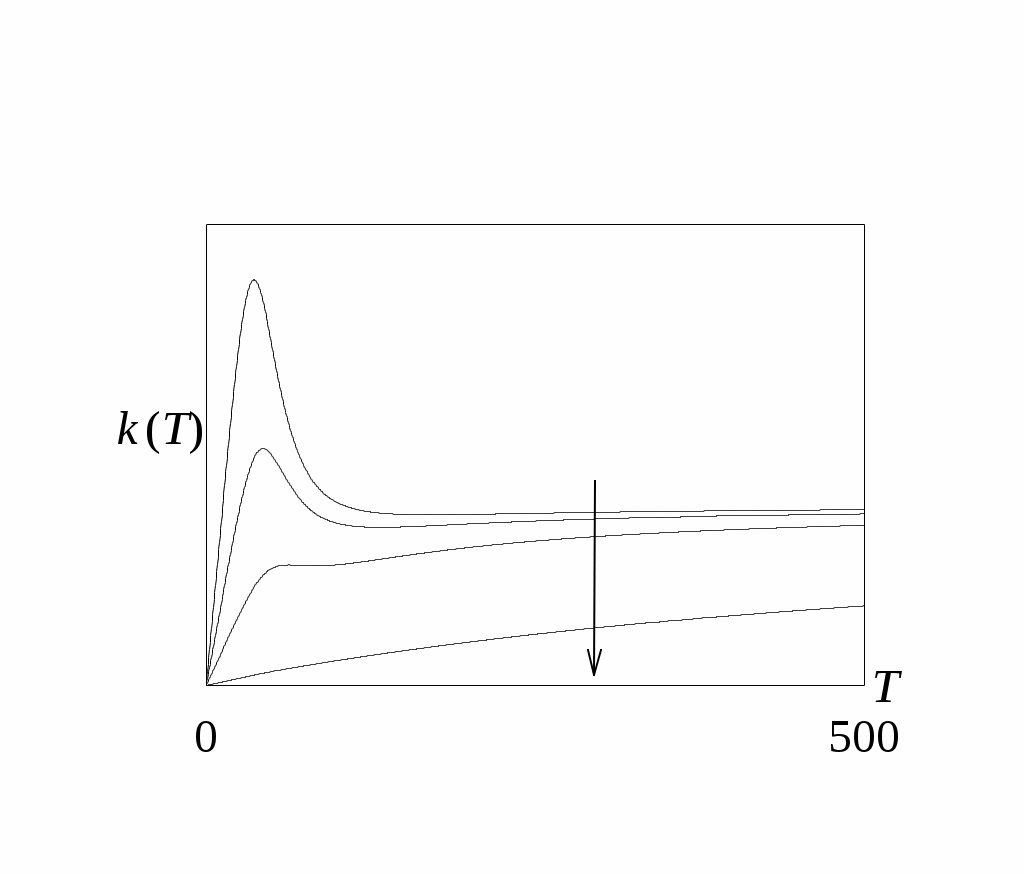
Рис. 6.2 Рис. 6.3

Задание 7. Рассчитать и построить зависимость электропроводности от толщины металлической пленки при заданной температуре. (Приложение MCAD №4)

Если уменьшать один из линейных размеров образца, т.е. переходить к определению электропроводности пленки, необходимо учитывать так называемые размерные эффекты.

Квантовый размерный эффект может возникать в пленках, толщина которых сравнима с длиной волны де Бройля.

При толщине металлической пленки соизмеримой со средней длиной свободного пробега, границы пленки накладывают ограничение на движение электронов проводимости. Возникающие при этом физические эффекты называются классическими размерными эффектами.

Различают зеркальное и диффузное отражение электронов от границ поверхности. Коэффициент зеркальности p зависит от шероховатости поверхности и определяется отношением зеркально отраженных электронов к полному числу электронов, падающих на поверхность.

Электропроводность тонкой пленки как функция толщины d определяется следующим интегральным выражением:

,

где: σ_пл и σ_беск электропроводность пленки и электропроводность бесконечно толстого (объемного) образца, ρ_пл и ρ_беск – соответствующие значения удельного сопротивления, – безразмерная толщина, γ =d / λ

---

Смотрите также файлы

• Реализация потребностей молодежи в волонтерской деятельности щербакова А. И.pptx

• Практическая работа 3 по теме Особенности конструирования современного урока математики.docx

• Практическая работа 3 Особенности конструирования современного урока.docx

• Образовательная программа робототехника.pdf

• Тест Основы вик. Оптические свойства глаза.docx