Файл: Методические указания к решению задач на практических занятиях по дисциплине Основы электроники и радиоматериалы К. т н. доцент Ситникова М. Ф.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.01.2024
Просмотров: 191
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
,беск, λ,беск - средняя длина свободного пробега бесконечно толстого образца, a - параметр, определяемый углом отражения электронов от границ поверхности.
На практике для расчета электропроводности как функции толщины используют приближенные выражения
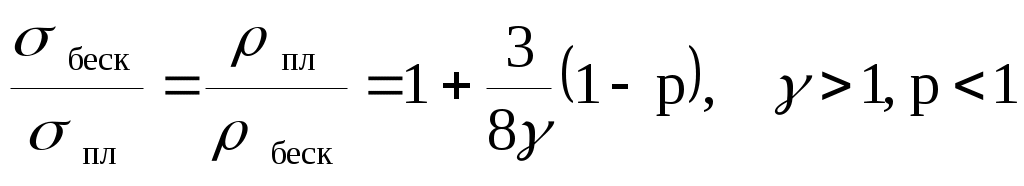, (7.1)
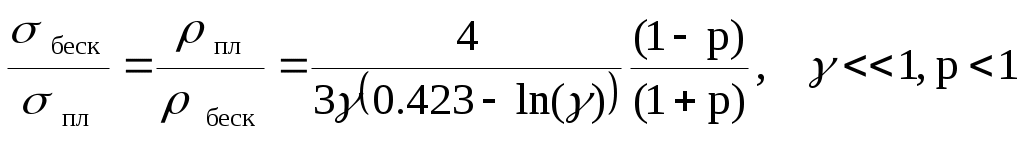, (7.2)
Отметим, что последнее из приведенных соотношение справедливо лишь для малых значений p и γ < 0.5.
При зеркальном отражении электронов от поверхности (p= 1) угол падения электронов на поверхность равен углу отражения от поверхности, и проекции импульса электрона в направлении электрического поля, приложенного к образцу, сохраняются, а следовательно, электропроводность образца не меняется.
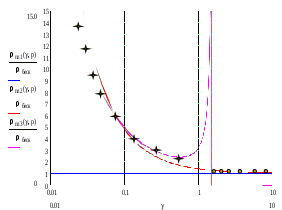
Рис.7.1 Зависимость удельного сопротивления пленки от толщины (в относительных координатах) р=0,3.
При диффузном отражении угол отражения может быть произвольным и равновероятно меняться от 0 до π. Количественное изменение электропроводности в этом случае учитываются выражениями (7.1) и (7.2) как функции параметра p.
ρпл (d,p,T)
Задача 7.2. Рассчитать удельное сопротивление пленки алюминия толщиной d = 1000 Ǻ, p = 0.5 при T = 77K.
Для Al из П.1. находим a = 4.05Ǻ, TD = 394K, Tпл = 933K.
В нашей задаче p = 0,5, что соответствует равенству диффузного и зеркального отражения
Средняя длина свободного пробега при T< TD (7.3) для объемного образца:
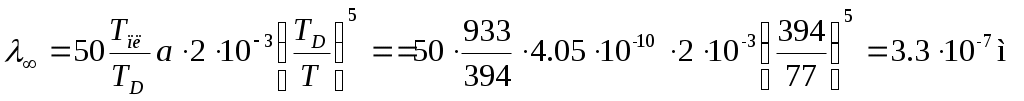
Полученное значение λ∞>d; выбираем для расчета формулу (7.4):
.
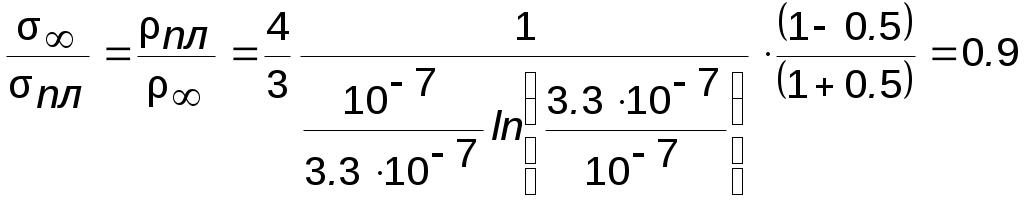Из П.1. для Alρ∞=0.3мкОм·см, следовательно, искомое удельное сопротивление пленки ρпл ≈ ρ∞ = 0.3мкОм·см.
Пример 6.5. Рассчитать электропроводность собственного Si при T=77K и T=300K.
Электропроводность полупроводников с концентрацией электронов n0, дырок p0 и подвижностью электронов и дырок соответственно μn и μp определяется как:
σ = en0μn +ep0μp (6.8)
Зависимость σ(T) определяется температурными зависимостями концентраций
n0(T), p0(T) и подвижностью μn(T), μp(T).
Концентрации электронов n0(T) и дырок p0(T)при температуре T в собственном невырожденном полупроводнике определяются выражениями
; (6.9)
,
(6.10)
где h – постоянная Планка, EF(T) – энергия Ферми при температуре T; EG – ширина запрещенной зоны; k – постоянная Больцмана; m"p, m"n – эффективные массы дырок и электронов соответственно. Если m0= m"p=m"n и EG – ширина запрещенной зоны равна 1,2 эВ, получаем искомую зависимость для вычисления концентрации электронов n0(T) и дырок p0(T)при заданных температурах.
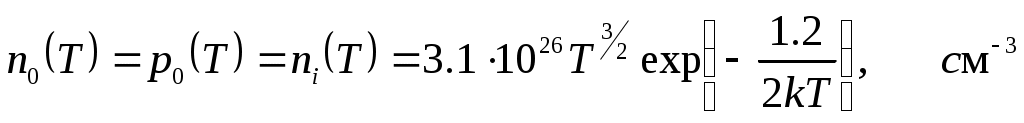
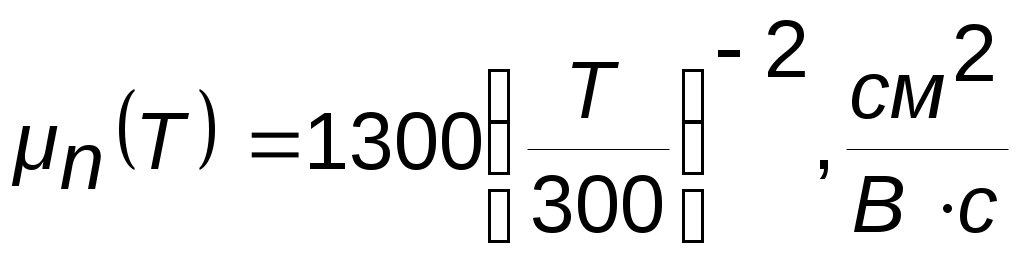(6.11)
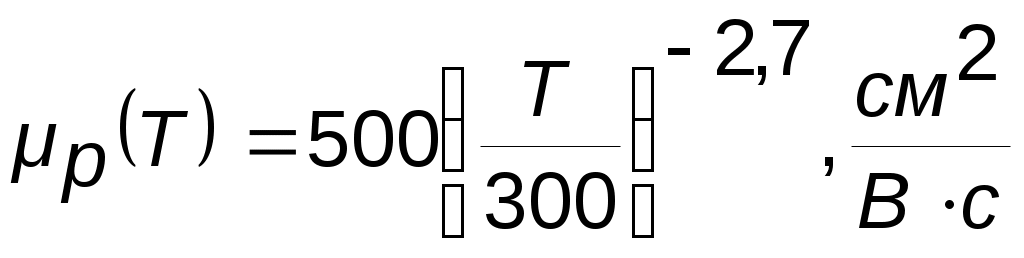
(6.12)
Выражения (6.10), 6(511) учитывают рассеяние электронов и дырок на тепловых колебаниях решетки. Последние три формулы дают возможность рассчитать электропроводность собственного Si при T=77K и T=300K.
Для нашей задачи:
ni(300) = 1.2∙1010 см–3, ni(77) = 0.6∙1010 см–3,
μn(300) = 1350 см2/(В∙с), μn(300) = 10400 см2/(В∙с),
μp(300) = 480 см2/(В∙с), μp(77) = 11000 см2/(В∙с),
σ(300) = 0.36 (Ом∙м)–1, σ(77) = 1.6 (Ом∙м)–1.
Пример 6.6. Определить электропроводность дырочного кремния с концентрацией носителей p=1015см–3 и подвижностью носителей μp=480см2/(В∙с) при T=300K.
Электропроводность полупроводников с концентрацией электронов n(T)и дырок p(T)и с подвижностью электронов и дырок, соответственно, μn(T) и μp(T) определяется как
.
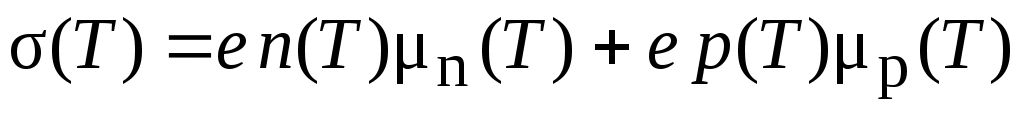Для примесного (донорного) полупроводника концентрация электронов проводимости nd(T) дается приближенным выражением в области возрастания примесной электропроводности при T≥T1 (рис.6.4):
, (6.13)
где Nd– концентрация донорной примеси; Eg – энергия активации примеси.
В области истощения примеси при T≤T2:
nd(T)=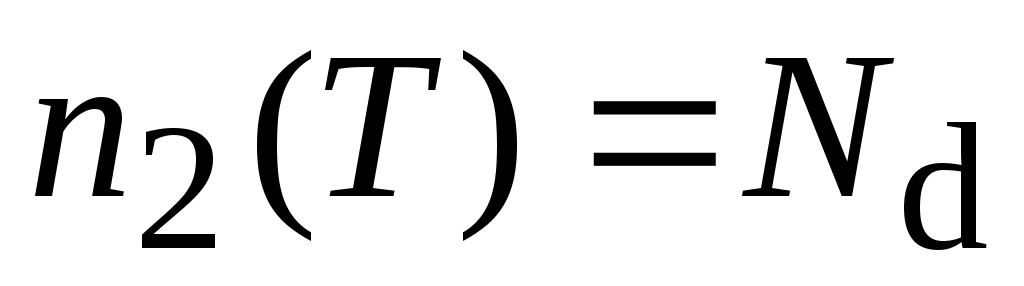
. (6.14)
Полная концентрация электронов
n(T)= n0(T) + nd(T)
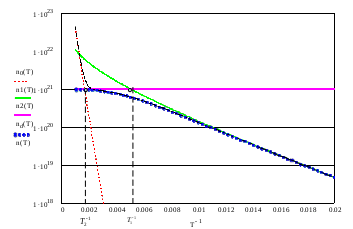
Рис. 6.4
На рисунке 6.4 в логарифмическом масштабе приведены представленные ранее зависимости, а также температурная зависимость полной концентрации электронов для донорного полупроводника.
Апроксимационные зависимости μn(T) и μp(T), как и прежде, имеют вид 6.11 и 6.12. Для электронного или дырочного полупроводника (5.8) упрощается, т.е. в условиях нашей задачи получаем
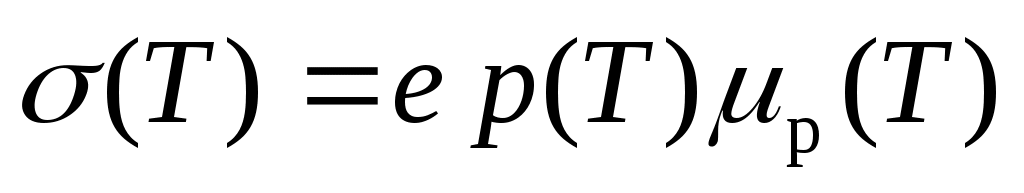=σp=1.6∙10–19∙1021∙480∙10–4 =7.7 (Ом∙м)–1
Задание 8. Рассчитать зависимости энергии Ферми и термодинамической работы выхода для примесного полупроводника от температуры.
Построить энергетическую диаграмму заданной пары металл-полупроводник в выбранном масштабе для случаев: без смещения, при прямом и обратном смещениях.
Рассчитать вольтамперную характеристику контакта в данном диапазоне температур. (Приложение MCAD №6)
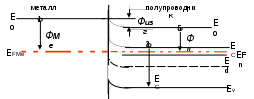
Энергия Ферми и термодинамическая работа выхода для собственного и примесного полупроводников в зависимости от температуры определяются выражениями (рис.8):
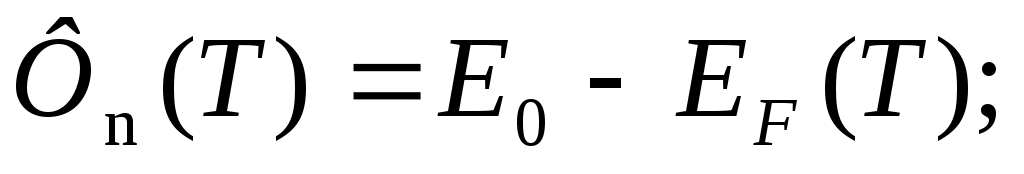
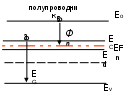
Рис.8
Рассмотрим контакт металл - полупроводник. Если приповерхностная область полупроводника обеднена основными носителями, то в области контакта со стороны полупроводника формируется область пространственного заряда ионизованных доноров или акцепторов и реализуется блокирующий контакт, или барьер Шоттки. В полупроводниковых приборах наибольшее применение получили блокирующие контакты металл - полупроводник или барьеры Шоттки.
Для контакта металл - полупроводник n-типа выберем условие, чтобы термодинамическая работа выхода из полупроводника Ф
п/п была меньше чем термодинамическая работа выхода из металла ФМе. В этом случае согласно уравнению (8.1) ток термоэлектронной эмиссии с поверхности полупроводника jп/п будет больше, чем ток термоэлектронной эмиссии с поверхности металла:
ФМе > Фп/п
При контакте таких материалов в начальный момент времени ток из полупроводника в металл будет превышать обратный ток из металла в полупроводник, и в приповерхностных областях полупроводника и металла будут накапливаться объемные заряды - отрицательные в металле и положительные в полупроводнике. В области контакта возникнет электрическое поле, в результате чего произойдет изгиб энергетических зон. Вследствие эффекта поля термодинамическая работа выхода на поверхности полупроводника возрастет. Этот процесс будет проходить до тех пор, пока в области контакта не выровняются токи термоэлектронной эмиссии и соответственно значения термодинамических работ выхода на поверхности. На рисунке 6.1 показаны зонные диаграммы различных этапов формирования контакта металл - полупроводник. В условиях равновесия в области контакта токи термоэлектронной эмиссии выровнялись, вследствие эффекта поля возник потенциальный барьер, высота которого равна разности термодинамических работ выхода: eφк = ФМе - Фп/п.Для контакта металл - полупроводник p-типа выберем условие, чтобы термодинамическая работа выхода из полупроводника Фп/п была больше, чем термодинамическая работа выхода из металла ФМе. В этом случае ток термоэлектронной эмиссии с поверхности полупроводника jп/п будет меньше, чем ток термоэлектронной эмиссии с поверхности металла согласно уравнению (6.1). При контакте таких материалов в начальный момент времени ток из металла в полупроводник p-типа будет превышать обратный ток из полупроводника в металла, и в приповерхностных областях полупроводника и металла будут накапливаться объемные заряды - положительные в металле и отрицательные в полупроводнике.
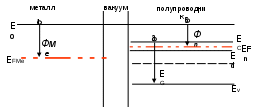
а)
b)
Рис. 8.1. Зонная диаграмма, иллюстрирующая образование барьера Шоттки
а) при отсутствии контакта, b) при контакте (без смещения)
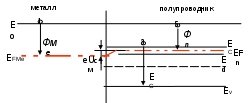
Рис. 8.2. Зонная диаграмма барьера Шоттки в случае прямого смещения (режим плоских зон)
Пример 8.1. Для заданной пары металл-полупроводник рассчитать и построить энергетическую диаграмму
барьера Шоттки и вольт-амперную характеристику контакта в данном диапазоне температур.
Ток термоэлектронной эмиссии с поверхности любого твердого тела определяется уравнением Ричардсона:
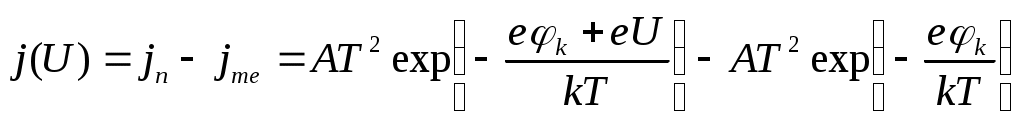
(8.1)
где: eφк = ФМе - Фп/п , Φ - работа выхода металла и полупроводника соответственно, А- константа Ричардсона,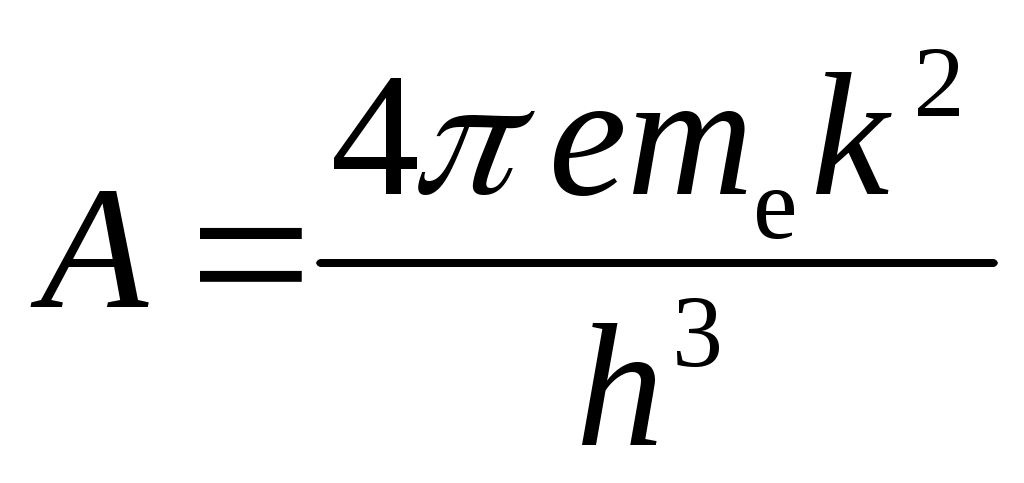
, me – масса электрона.
Вольтамперную характеристику контакта металл–полупроводник можно представить в виде (рис.8.2):
,
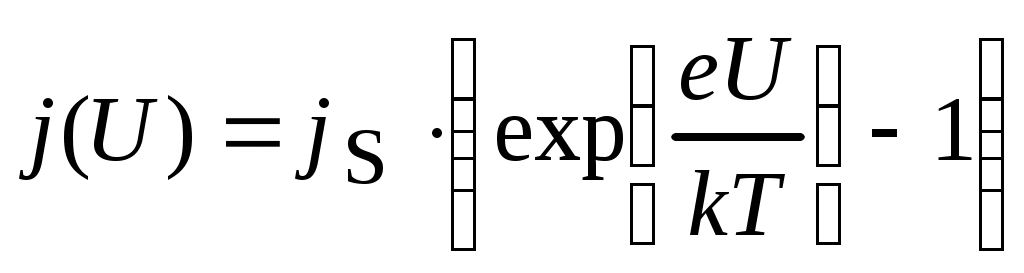где e – заряд электрона; j S – плотность тока насыщения. Для контакта металл–полупроводник плотность тока насыщения можно представить в виде
,
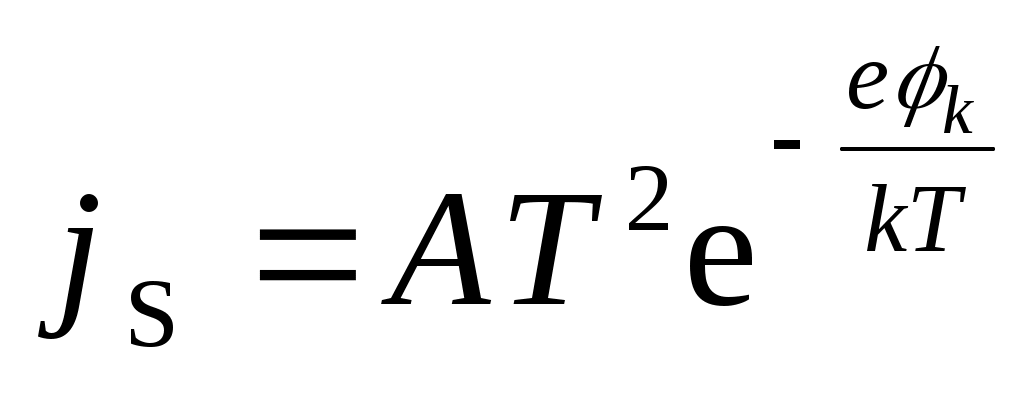где φк – контактная разность потенциалов.
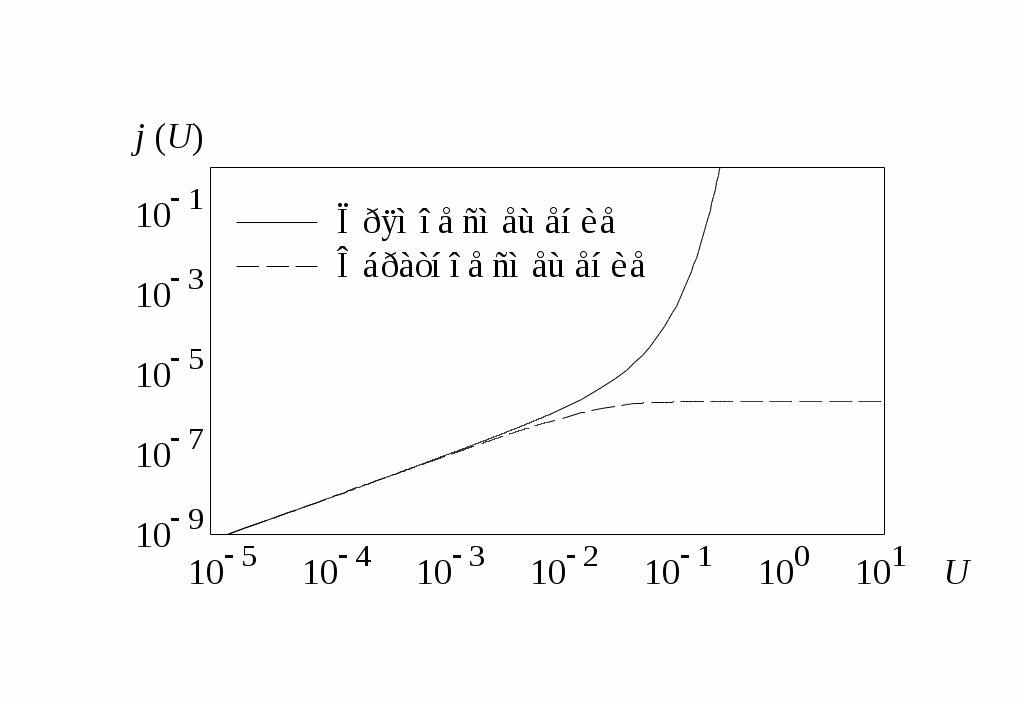
Рис. 9.2
Задание 9. Рассчитать концентрацию носителей заряда в заданном полупроводнике для создания омического контакта к металлу.
Омический контакт — контакт между металлом и полупроводником, характеризующийся линейной и симметричной вольт-амперной характеристикой (Рис.9.1). Такую ВАХ можно получить в случае обогащения приконтактного слоя основными носителями, что возможно при ФМе < Фп/п ..
Однако на практике такого соотношения между работой выхода металла и полупроводника достичь сложно. В модели барьера Шоттки выпрямление зависит от разницы между работой выхода металла и электронного сродства полупроводника Кроме того, контакты металл-полупроводник в действительности, точно не следуют модели Шоттки, так как наличие внешних поверхностных состояний на границе раздела фаз (например, оксиды и дефекты) может сделать поведение перехода практически не зависящим от разницы между работой выхода металла и электронного сродства.
Поэтому идут по другому пути. В производстве полупроводниковых приборов и интегральных схем, для создания
На практике для расчета электропроводности как функции толщины используют приближенные выражения
, (7.1) , (7.2)Отметим, что последнее из приведенных соотношение справедливо лишь для малых значений p и γ < 0.5.
При зеркальном отражении электронов от поверхности (p= 1) угол падения электронов на поверхность равен углу отражения от поверхности, и проекции импульса электрона в направлении электрического поля, приложенного к образцу, сохраняются, а следовательно, электропроводность образца не меняется.
Рис.7.1 Зависимость удельного сопротивления пленки от толщины (в относительных координатах) р=0,3.
При диффузном отражении угол отражения может быть произвольным и равновероятно меняться от 0 до π. Количественное изменение электропроводности в этом случае учитываются выражениями (7.1) и (7.2) как функции параметра p.
ρпл (d,p,T)
Задача 7.2. Рассчитать удельное сопротивление пленки алюминия толщиной d = 1000 Ǻ, p = 0.5 при T = 77K.
Для Al из П.1. находим a = 4.05Ǻ, TD = 394K, Tпл = 933K.
В нашей задаче p = 0,5, что соответствует равенству диффузного и зеркального отражения
Средняя длина свободного пробега при T< TD (7.3) для объемного образца:
Полученное значение λ∞>d; выбираем для расчета формулу (7.4):
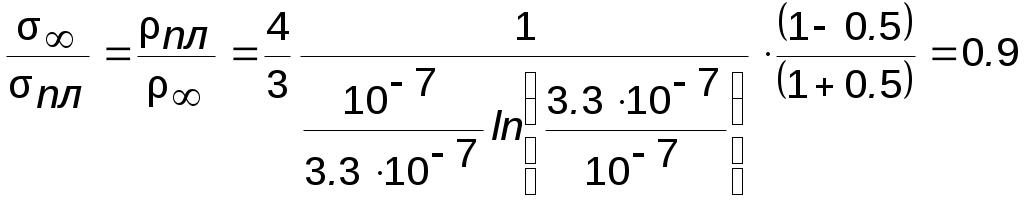.Из П.1. для Alρ∞=0.3мкОм·см, следовательно, искомое удельное сопротивление пленки ρпл ≈ ρ∞ = 0.3мкОм·см.
Пример 6.5. Рассчитать электропроводность собственного Si при T=77K и T=300K.
Электропроводность полупроводников с концентрацией электронов n0, дырок p0 и подвижностью электронов и дырок соответственно μn и μp определяется как:
σ = en0μn +ep0μp (6.8)
Зависимость σ(T) определяется температурными зависимостями концентраций
n0(T), p0(T) и подвижностью μn(T), μp(T).
Концентрации электронов n0(T) и дырок p0(T)при температуре T в собственном невырожденном полупроводнике определяются выражениями
; (6.9)
,
(6.10)
где h – постоянная Планка, EF(T) – энергия Ферми при температуре T; EG – ширина запрещенной зоны; k – постоянная Больцмана; m"p, m"n – эффективные массы дырок и электронов соответственно. Если m0= m"p=m"n и EG – ширина запрещенной зоны равна 1,2 эВ, получаем искомую зависимость для вычисления концентрации электронов n0(T) и дырок p0(T)при заданных температурах.
(6.11) (6.12)
Выражения (6.10), 6(511) учитывают рассеяние электронов и дырок на тепловых колебаниях решетки. Последние три формулы дают возможность рассчитать электропроводность собственного Si при T=77K и T=300K.
Для нашей задачи:
ni(300) = 1.2∙1010 см–3, ni(77) = 0.6∙1010 см–3,
μn(300) = 1350 см2/(В∙с), μn(300) = 10400 см2/(В∙с),
μp(300) = 480 см2/(В∙с), μp(77) = 11000 см2/(В∙с),
σ(300) = 0.36 (Ом∙м)–1, σ(77) = 1.6 (Ом∙м)–1.
Пример 6.6. Определить электропроводность дырочного кремния с концентрацией носителей p=1015см–3 и подвижностью носителей μp=480см2/(В∙с) при T=300K.
Электропроводность полупроводников с концентрацией электронов n(T)и дырок p(T)и с подвижностью электронов и дырок, соответственно, μn(T) и μp(T) определяется как
.Для примесного (донорного) полупроводника концентрация электронов проводимости nd(T) дается приближенным выражением в области возрастания примесной электропроводности при T≥T1 (рис.6.4):
, (6.13)
где Nd– концентрация донорной примеси; Eg – энергия активации примеси.
В области истощения примеси при T≤T2:
nd(T)=
. (6.14)Полная концентрация электронов
n(T)= n0(T) + nd(T)
Рис. 6.4
На рисунке 6.4 в логарифмическом масштабе приведены представленные ранее зависимости, а также температурная зависимость полной концентрации электронов для донорного полупроводника.
Апроксимационные зависимости μn(T) и μp(T), как и прежде, имеют вид 6.11 и 6.12. Для электронного или дырочного полупроводника (5.8) упрощается, т.е. в условиях нашей задачи получаем
=σp=1.6∙10–19∙1021∙480∙10–4 =7.7 (Ом∙м)–1Задание 8. Рассчитать зависимости энергии Ферми и термодинамической работы выхода для примесного полупроводника от температуры.
Построить энергетическую диаграмму заданной пары металл-полупроводник в выбранном масштабе для случаев: без смещения, при прямом и обратном смещениях.
Рассчитать вольтамперную характеристику контакта в данном диапазоне температур. (Приложение MCAD №6)
Энергия Ферми и термодинамическая работа выхода для собственного и примесного полупроводников в зависимости от температуры определяются выражениями (рис.8):
Рис.8
Рассмотрим контакт металл - полупроводник. Если приповерхностная область полупроводника обеднена основными носителями, то в области контакта со стороны полупроводника формируется область пространственного заряда ионизованных доноров или акцепторов и реализуется блокирующий контакт, или барьер Шоттки. В полупроводниковых приборах наибольшее применение получили блокирующие контакты металл - полупроводник или барьеры Шоттки.
Для контакта металл - полупроводник n-типа выберем условие, чтобы термодинамическая работа выхода из полупроводника Ф
п/п была меньше чем термодинамическая работа выхода из металла ФМе. В этом случае согласно уравнению (8.1) ток термоэлектронной эмиссии с поверхности полупроводника jп/п будет больше, чем ток термоэлектронной эмиссии с поверхности металла:
ФМе > Фп/п
При контакте таких материалов в начальный момент времени ток из полупроводника в металл будет превышать обратный ток из металла в полупроводник, и в приповерхностных областях полупроводника и металла будут накапливаться объемные заряды - отрицательные в металле и положительные в полупроводнике. В области контакта возникнет электрическое поле, в результате чего произойдет изгиб энергетических зон. Вследствие эффекта поля термодинамическая работа выхода на поверхности полупроводника возрастет. Этот процесс будет проходить до тех пор, пока в области контакта не выровняются токи термоэлектронной эмиссии и соответственно значения термодинамических работ выхода на поверхности. На рисунке 6.1 показаны зонные диаграммы различных этапов формирования контакта металл - полупроводник. В условиях равновесия в области контакта токи термоэлектронной эмиссии выровнялись, вследствие эффекта поля возник потенциальный барьер, высота которого равна разности термодинамических работ выхода: eφк = ФМе - Фп/п.Для контакта металл - полупроводник p-типа выберем условие, чтобы термодинамическая работа выхода из полупроводника Фп/п была больше, чем термодинамическая работа выхода из металла ФМе. В этом случае ток термоэлектронной эмиссии с поверхности полупроводника jп/п будет меньше, чем ток термоэлектронной эмиссии с поверхности металла согласно уравнению (6.1). При контакте таких материалов в начальный момент времени ток из металла в полупроводник p-типа будет превышать обратный ток из полупроводника в металла, и в приповерхностных областях полупроводника и металла будут накапливаться объемные заряды - положительные в металле и отрицательные в полупроводнике.
а)
b)
Рис. 8.1. Зонная диаграмма, иллюстрирующая образование барьера Шоттки
а) при отсутствии контакта, b) при контакте (без смещения)
Рис. 8.2. Зонная диаграмма барьера Шоттки в случае прямого смещения (режим плоских зон)
Пример 8.1. Для заданной пары металл-полупроводник рассчитать и построить энергетическую диаграмму
барьера Шоттки и вольт-амперную характеристику контакта в данном диапазоне температур.
Ток термоэлектронной эмиссии с поверхности любого твердого тела определяется уравнением Ричардсона:
(8.1)
где: eφк = ФМе - Фп/п , Φ - работа выхода металла и полупроводника соответственно, А- константа Ричардсона,
, me – масса электрона.Вольтамперную характеристику контакта металл–полупроводник можно представить в виде (рис.8.2):
,где e – заряд электрона; j S – плотность тока насыщения. Для контакта металл–полупроводник плотность тока насыщения можно представить в виде
, где φк – контактная разность потенциалов.
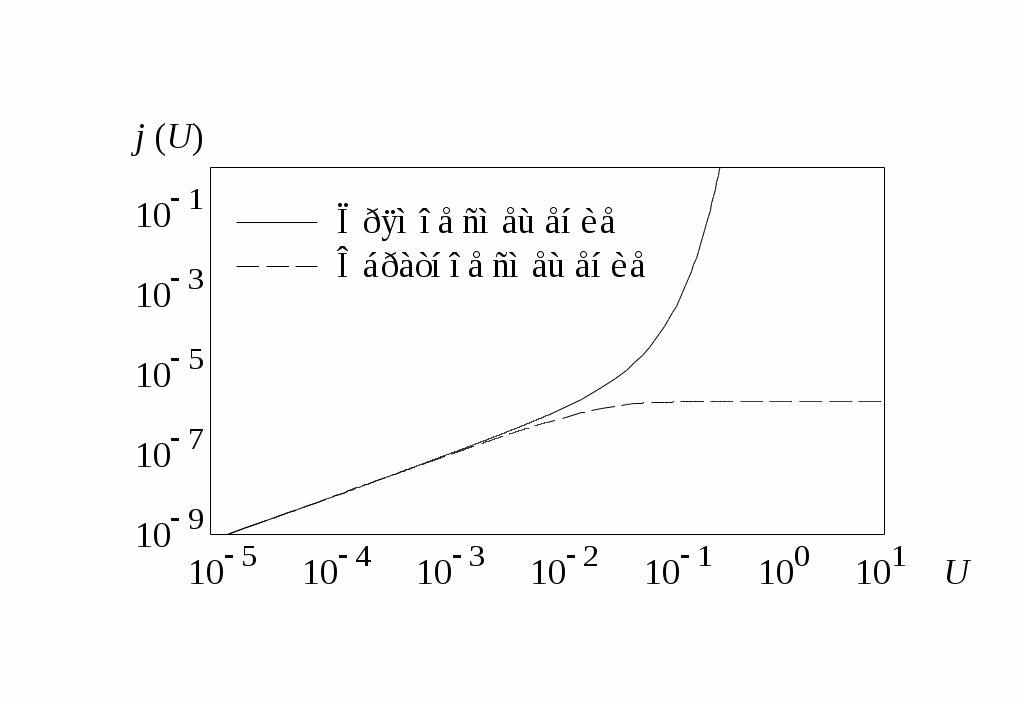
Рис. 9.2
Задание 9. Рассчитать концентрацию носителей заряда в заданном полупроводнике для создания омического контакта к металлу.
Омический контакт — контакт между металлом и полупроводником, характеризующийся линейной и симметричной вольт-амперной характеристикой (Рис.9.1). Такую ВАХ можно получить в случае обогащения приконтактного слоя основными носителями, что возможно при ФМе < Фп/п ..
Однако на практике такого соотношения между работой выхода металла и полупроводника достичь сложно. В модели барьера Шоттки выпрямление зависит от разницы между работой выхода металла и электронного сродства полупроводника Кроме того, контакты металл-полупроводник в действительности, точно не следуют модели Шоттки, так как наличие внешних поверхностных состояний на границе раздела фаз (например, оксиды и дефекты) может сделать поведение перехода практически не зависящим от разницы между работой выхода металла и электронного сродства.
Поэтому идут по другому пути. В производстве полупроводниковых приборов и интегральных схем, для создания