Файл: 1. выбор на основе классического определения вероятности.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.01.2024
Просмотров: 93
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
1. ВЫБОР на основе классического
определения вероятности
1.1. Основы выбора на базе классического
определения вероятности
Пусть имеется n элементов, различающихся свойствами или качествами. Причем среди них r элементов одного типа, lэлементов другого типа и т.д., q элементов последнего типа, так что выполняется условие
n = r + l + … + q.
Случайным образом отбирают m элементов, причем порядок выбора не важен, важен только состав отобранной группы элементов. Вероятность того, что в отобранной группе оказалось kэлементов первого типа, jэлементов второго типа и т. д., i элементов последнего типа, так чтобы
m = k + j + … + i,
вычисляется по формуле
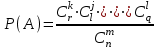 , (1.1)
, (1.1) где
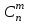 ‑ число сочетаний из n элементов по m:
‑ число сочетаний из n элементов по m: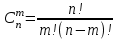 . (1.2)
. (1.2)Полезно знать и уметь использовать следующие свойства сочетаний:
1.
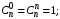
2.
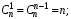 (1.3)
(1.3)3.
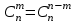 .
.1.2. Решение типового задания по теме «Выбор на основе
классического определения вероятности»
Задание № 1. В академической группе 10 студентов проживают в Санкт-Петербурге, 7 приехали из других городов России и 3 иностранца. На прием в деканат пришли 5 студентов из этой группы. Найти вероятности событий:
А. Все – из Санкт-Петербурга.
В. 2 – из других городов России и 3 иностранца.
С. 3 – из Санкт-Петербурга, 1 – из другого города России и 1 иностранец.
D. Все иностранцы пришли на прием.
Решение. Поскольку порядок выбора не важен в условиях задачи, то пользуемся формулой (1.1).
Определим значения параметров: n= 20, m= 5, r = 10, l= 7, q= 3.
Найдем Р(А). Изобразим графически схему выбора. В левом блоке – общее число участников выбора (20) и их распределение по трем категориям – жители Петербурга, другие россияне и иностранцы (10 + 7 + 3). Стрелки означают выбор. Стрелка слева направо показывает выбор общего числа, вне зависимости от категорий. Стрелки сверху вниз указывают на конкретный выбор из каждой категории.
| 2  0 0 | | 5 | ||
| 1 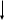 0 0 | 7 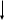 | 3 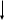 | | |
| | | | | |
| 5 | 0 | 0 | | |
Тогда параметрызадачи принимают значения:k= 5, j=i= 0.
Тогда
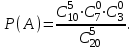
Вычислим
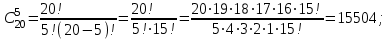
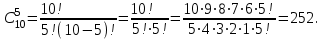
В соответствии со свойствами сочетаний
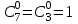 .
.Тогда
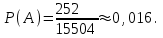
Найдем Р(В). Изобразим графически схему выбора
| 2  0 0 | | 5 | ||
| 1  0 0 | 7  | 3 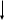 | | |
| | | | | |
| 0 | 2 | 3 | | |
Тогда параметрызадачи принимают значения: k= 0, j= 2, i= 3.
Тогда

Вычислим
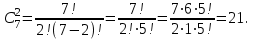
В соответствии со свойствами сочетаний
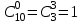 .
. Тогда
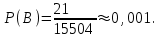
Найдем Р(С). Изобразим графически схему выбора
| 2  0 0 | | 5 | ||
| 1  0 0 | 7  | 3  | | |
| | | | | |
| 3 | 1 | 1 | | |
Тогда параметрызадачи принимают значения: k= 3, j= 1, i= 1.
Тогда
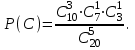
Вычислим
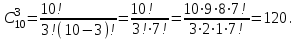
В соответствии со свойствами сочетаний
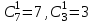 .
.Тогда
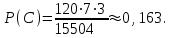
Вычисленные вероятности событий А, В и Свполне подтверждаются обыденной логикой. Например, студенты из Санкт-Петербурга составляют половину всей академической группы и не встретить их около деканата среди других студентов этой группы – маловероятное событие. Действительно, вероятность события В– наименьшая из всех вычисленных, в частности она приблизительно в 160 раз меньше ближайшей к ней по значению вероятности события С.
Для того, чтобы найти Р(D), необходимо изменить схему выбора. Действительно, на прием в деканат пришли все иностранцы, т.е. 3 из 3. Для ответа на вопрос задачи не важно, какие именно 2 других студента пришли на прием. То есть выбор производится из двух категорий: «иностранцы» и «не иностранцы». Поэтому исходные параметры таковы:
n= 20, m= 5, r = 3, l= 17 (количество «не иностранцев» l= 20 – 3 = 17). Графическая схема выбора такова:
| 2  0 0 | | 5 | ||
| 3  | 1  7 7 | | | |
| | | | | |
| 3 | 2 | | ||
Тогда параметрызадачи принимают значения: k= 3, j= 2.
Тогда
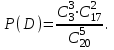
Вычислим
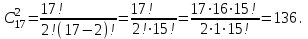
В соответствии со свойствами сочетаний
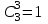 .
.Тогда
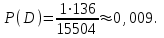
Действительно, выбор всей малочисленной категории с математической точки зрения маловероятен, что и демонстрирует значение вероятности события D.
Задания по теме «Выбор на основе классического
определения вероятности»
| 1. В художественной галере из 16 картин – 7 подделок. Коллекционер случайно выбрал 3 картины. Найти вероятности событий: А – все картины – подделки, В – 1 подлинная и 2 подделки, С – 2 подлинные и 1 подделка, D – все картины подлинные. | 2. На экзамене по курсу – 20 вопросов. Студент знает 12 из них. Каковы вероятности, что в вытащенном на экзамене билете: А – нет знакомых вопросов, В – 1 знакомый вопрос, С – 2 знакомых вопроса, D – все 3 вопроса знакомы. | |
| | | |
| 3. В результате 20 переговоров были заключены 4 сделки, что соответствует уровню успешности переговоров 20%. Найти вероятности, что в 5 анализируемых переговорах было заключено: А – 5 сделок, В – 4 сделки, С – 2 сделки. | 4. На прием к врачу пришли 20 иностранных студентов, из них 10 из Китая, 5 – из других стран Азии, 4 – из Африки, 1 – из Европы. 5 из них были госпитализированы. Найти вероятности, что это: А – все китайцы, В – 2 китайца, 1 другой азиат, 1 африканец и 1 европеец. | |
| 5. В репертуаре театра 20 спектаклей, из них 12 – успешных, 5 – средних, остальные – провальные. Купили 4 билета на разные спектакли. Найти вероятности событий: А – все спектакли успешные, В – 2 спектакля успешных, 1 средний и 1 провальный, С – 1 спектакль средний, остальные – провальные. | 6. Фирма ведет 14 проектов. Из них 8 – международные, 4 – общероссийские, 2 – городские. Для презентации взяли 4 проекта. Каковы вероятности событий: А – все проекты международные, В – 2 проекта международных, 1 российский и 1 городской, С – 3 проекта российских и 1 городской. | |
| | |
| 7. Покупатель отобрал по каталогу фирмы 18 коттеджей: 10 одноэтажных, 5 двухэтажных, остальные – трехэтажные. За день он осмотрел 5 коттеджей в поселке «Высота». Найти вероятность, что он осмотрел коттеджи: А – все одноэтажные, В – 3 одноэтажных и 2 двухэтажных, С – все трехэтажные, D – 2 двухэтажных и все трехэтажные. | 8. В отделе академических обменов есть 20 вакансий на семестр. Из них 15 – в Финляндию, 4 – в Германию и 1 – в США. 5 студентов экономического факультета стали участниками обмена. Найти вероятности, что они поехали учиться: А – все в Финляндию, В – 4 в Финляндию и 1 в Германию, С – 1 в Финляндию, 3 в Германию и 1 в США. D – все не в Финляндию. |
| 9. 10 студентов группы из 20 человек сдали математику в сессию, 6 - в допсессию, а остальные – на комиссии. Найти вероятность, что среди 6 друзей сдали экзамен: А – все на допсессии, В – все в сессию, С – 4 на комиссии, D – 3 в сессию, 2 надопсессии и 1 на комиссии. | 10. В общежитии есть по одному свободному месту в 2 одноместных номерах, 5 в двухместных и 8 в трехместных. По обмену на семестр приехали 5 иностранных студентов. Найти вероятности, что они разместились: А – все в трехместных номерах, В – 1 – в одноместном, 3 – в двухместных и 1 - в трехместном, С – все в двухместных. |