Файл: Разработка программы, реализующей алгоритмы сортировки и поиска.docx
Добавлен: 12.01.2024
Просмотров: 175
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
2).
2. Сортировка пузырьком реализует алгоритм сравнения пар значений при полном прохождении списка, если первое значение больше второго в паре, происходит обмен этих же значений. Максимальные отсортированные значения в итоге оказываются в конце списка, и не затрагиваются при дальнейшей сортировке. Преимуществом такого алгоритма сортировки является простота реализации, а минусом – крайне медленная скорость работы метода, если более мелкие значения находятся в конце списка, то алгоритм затрачивает довольно много времени, чтобы их переместить ближе к началу списка. Затрачиваемое время сортировки данных в лучшем случае – O(n), в худшем случае – O(n2). Хоть и сортировка не используется на данный момент, кроме как в учебных целях, тем не менее, ее принципы используются в сортировке шейкером(перемешиванием).
3. Сортировка шейкером(перемешиванием) реализует алгоритм двунаправленной сортировки, в отличие от пузырьковой, которая реализует только однонаправленную сортировку значений. Принцип сортировки тот же, отличие только в том, что алгоритм перемещается по значениям сначала слева направо, а потом справа налево. В данном случае, устраняется проблема пузырьковой сортировки – медленное время работы, при наличии минимальных значений в конце списка. Ведь при прохождении алгоритмом списка справа налево, эти же значения будут отодвигаться в начало списка. Затрачиваемое время сортировки данных в лучшем случае - O(n), в худшем случае – O(n2). Хоть и теоретически время сортировки совпадает с пузырьковой, однако в реальной работе, и с большими списками, сортировка шейкером показывает себя лучше.
4. Сортировка вставками реализует алгоритм перемещения нужного значения в начало списка, при полном прохождении списка. Данный метод сортировки обрабатывает элементы массива по порядку, все что находится слева от определенного индекса – уже отсортировано. Алгоритм в течение прохождения по списку, сравнивает второе значение с первым, если больше, ничего не делает, если меньше, производит так называемую вставку – вырезает элемент, весь, или часть списка сдвигаются вправо, и вырезанный элемент вставляется на нужное место. И крайнее значение отсортированного списка будет сравниваться с следующими значениями после него. Затрачиваемое время сортировки данных в лучшем случае – O(n) для сравнения, и O(1) для перестановок, а в худшем случае - O(n
2) для сравнений и перестановок. Отличие данного метода сортировки от предыдущих заключается в том, что для произведения вставки элементов, нужна дополнительно выделенная память.
5. Сортировка Шелла реализует усовершенствованный алгоритм вставками. Главным его отличием от сортировки вставками – сравнение элементов, стоящих не только рядом, но и на определенном расстоянии. Можно сказать, что это сортировка вставками с “грубыми” проходами, не требующими строгого задания шагов между элементами списка. Затрачиваемое время сортировки данных в лучшем случае - O(nlog2n), в худшем случае O(n2). Данный метод сортировки данных быстрее предыдущих, но медленнее быстрой сортировки, однако у нее есть и преимущества – отсутствие дополнительного потребления памяти, и даже при самых худших условиях, среднее время сортировки слабо изменяется.
6. Быстрая сортировка реализует совершенно иной алгоритм, с своими особенностями. Сначала из списка выбирается один элемент, который является опорным, другие элементы в списке распределяют и сортируют так, чтобы элементы меньше опорного оказались до него, а большие или такие же, после него. Затем, такой же алгоритм применяется рекурсивно для частей списка, находящихся слева и справа от опорного элемента. Такой метод сортировки списка значительно быстрее предыдущих, однако, зависит от выбора опорного элемента, при неправильном выборе, сортировка крайне медленна, и выполняется за O(n2) времени. Наилучшее же время сортировки – O(nlogn). Алгоритм отвечает типу – “разделяй и властвуй” (разделение списка на две части, и сортировка рекурсивно).
7. Сортировка слиянием реализует схожий принцип алгоритма быстрой сортировки. Происходит также деление списка на более мелкие части и сортировка их. Единственное отличие от быстрой сортировки – нет какого-либо опорного элемента, список делится пополам, и этот же процесс совершается рекурсивно для каждой части списка до тех пор, пока не будут отсортированы элементы, а затем эти же элементы будут вставлены обратно в верном порядке. Однако, у такого метода есть значительный минус – алгоритм выполняет все те же действия даже для частично отсортированного списка, что может повлиять на работу над такими списками. При таком раскладе, прочие методы сортировки справятся с списком значительно быстрее, чем сортировка слиянием. Сортировка слиянием использует тот же принцип, что и быстрая сортировка – “разделяй и властвуй”. Затрачиваемое время сортировки данных в лучшем случае – O(nlogn), в худшем случае все также – O(nlogn). Данный алгоритм довольно стабилен, однако он требует дополнительного выделения памяти под подсписки, которые возникают в процессе разделения и сортировки отдельных элементов, причем, процесс выделения памяти происходит постоянно, может произойти перевыделение памяти для списков.
8. Сортировка подсчетом реализует алгоритм с помощью подсчета, используется диапазон чисел сортируемого списка для подсчитывания количества совпадающих элементов. Такой метод применяется только в том случае, если значения подпадающие под алгоритм сортировки подсчетом, имеют сравнительно малый диапазон возможных значений по сравнению с сортируемым множеством. Как пример, сотни тысяч числовых значений, имеющих диапазон от 0 до 100. Обычные алгоритмы сортировки будут затрачивать в разы больше времени, чем сортировка подсчетом, которая каждое значение записывает в список отдельный, и так с каждым последующим значением. Однако, эта же сортировка крайне неэффективна для обычных списков, где диапазон значений схож с количеством их же.
9. Поразрядная сортировка реализует алгоритм сортировки целых числовых значений. Однако, такой алгоритм можно применить и для любых объектов, запись которых возможна с помощью деления на разряды. К этим данным можно отнести цифры, строки с набором символов, произвольные значения в памяти, которые представлены набором байтов. Сравнение в таких алгоритмах происходит с помощью разрядов, то есть, поразрядно, сравниваются значения одного крайнего разряда, и по этому результату сравнения, элементы группируются. Затем, значения следующих разрядов, и соседнего сравниваются, и опять элементы сортируются по порядку. Таким образом, алгоритм проходит до конца, до последнего разряда и сортирует все элементы. Затрачиваемое время сортировки данных в худшем случае – O(w*n), где w – это количество бит, которые требуется для хранения ключа, формула расхода памяти также аналогична [3].
Методы поиска
Для работы со структурами данных, необходима реализация алгоритмов поиска, ведь в значительно крупных списках, поиск нужного элемента осложняется, поиск вручную может занять множество времени. Исследования по нахождению новых методов поиска продолжаются и по сей день. Каждый алгоритм имеет свои плюсы и минусы, рассмотрим поподробнее основные методы поиска:
1. Последовательный поиск.
2. Бинарный поиск.
3. Интерполяционный поиск.
1. Последовательный поиск называется также линейным, является самым простым методом поиска. Алгоритм его реализуется следующим образом – указатель наводится на начало списка, и идет последовательно по всему списку, пока не будет найден нужный элемент, затем указатель будет остановлен. Главным его недостатком является низкая скорость при больших размерах списка, время работы пропорционально количеству элементов в структурах данных. Данный метод используется только в списках небольшого размера [4].
2. Бинарный поиск реализует алгоритм деления пополам, а затем сравнения среднего значения первого и второго частей списка с искомым значением, и при ближайшем совпадении, выбирается нужная часть списка, и поиск продолжается по такому же принципу. В конце концов, будет найден искомый элемент, либо же нет. Такой метод значительно быстрее работает при реализации поиска по спискам большого размера [5].
3. Интерполяционный поиск реализует алгоритм интерполирования, который подобен бинарному, но вместо деления области поиска на две равные части, интерполяционный поиск работает в отсортированном массиве значений, и сравнивает искомое значение с средним значением в части массива, если искомое значение меньше или больше части массива, он его отсекает, и продолжает поиск с таким же принципом до тех пор, пока не будет найдено искомое значение. Особенностью такого поиска является отсекание значительно больших значений, чем искомое, или значительно меньших, что позволяет сэкономить время и ресурсы. Данный алгоритм поиска определяется формулой 1 [6].
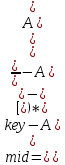 (1)
(1)
2. Список очередь
Цель курсового проекта – реализация списка типа очереди, как типа данных, а также реализация функций работы с ним: добавление и удаление элементов, поиск, открытие из файла и сохранение в файл.
Для определения структуры в программном коде C++, используется функция struct. Пример реализации односвязной структуры данных в виде списка изображен на рисунке 4. В данной структуре название списка: “node”. А int data и node*next – компоненты структуры.
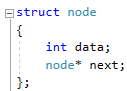
Рисунок 4 – Реализация структуры данных в виде списка
Целью курсовой работы является работа со списком типа очередь. Данный тип структуры данных представлен на рисунке 5 и работает по принципу FIFO – первый пришел, первый ушел.

Рисунок 5 – Список типа очереди
Добавление элементов в таких структурах данных происходит с конца списка, а удаление с начала. Очередь является динамической структурой, так как предполагает вставку и удаление элементов. Так как по заданию необходима реализация односвязного списка, то каждый элемент имеет только один указатель, на следующий элемент в списке, либо на конец.
2.1 Генерация очереди
Для генерации очереди и его элементов, была реализована функция Insert(), вставленная в цикл, зависящий от переменной int n, которая определяет размер списка, пример реализации генерации очереди представлен на рисунке 6.

Рисунок 6 – Генерация списка типа очереди
Переменная n задается пользователем, вводящим целочисленное значение с клавиатуры. В процессе генерации значений, используется функция rand(), которая производит случайную генерацию целочисленных значений, находящихся в промежутке от 0 до 99. Однако, эта же функция при повторных генерациях значений, берет те же самые значения из первой попытки генерации для правильной отладки разрабатываемой программы. Для полной рандомизации значений была использована функция srand(), которая при каждом запуске программы, генерирует совершенно новые случайные значения. Чтобы не менять каждый раз аргумент в функции srand(), используется функция time() в аргументах которой используется нулевой указатель - NULL, при выполнении time() с нулевым указателем, возвращается время системы, что обеспечивает полную рандомизацию значений при запуске программы. Реализация генерации случайных значений изображена на рисунке 7.
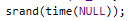
2. Сортировка пузырьком реализует алгоритм сравнения пар значений при полном прохождении списка, если первое значение больше второго в паре, происходит обмен этих же значений. Максимальные отсортированные значения в итоге оказываются в конце списка, и не затрагиваются при дальнейшей сортировке. Преимуществом такого алгоритма сортировки является простота реализации, а минусом – крайне медленная скорость работы метода, если более мелкие значения находятся в конце списка, то алгоритм затрачивает довольно много времени, чтобы их переместить ближе к началу списка. Затрачиваемое время сортировки данных в лучшем случае – O(n), в худшем случае – O(n2). Хоть и сортировка не используется на данный момент, кроме как в учебных целях, тем не менее, ее принципы используются в сортировке шейкером(перемешиванием).
3. Сортировка шейкером(перемешиванием) реализует алгоритм двунаправленной сортировки, в отличие от пузырьковой, которая реализует только однонаправленную сортировку значений. Принцип сортировки тот же, отличие только в том, что алгоритм перемещается по значениям сначала слева направо, а потом справа налево. В данном случае, устраняется проблема пузырьковой сортировки – медленное время работы, при наличии минимальных значений в конце списка. Ведь при прохождении алгоритмом списка справа налево, эти же значения будут отодвигаться в начало списка. Затрачиваемое время сортировки данных в лучшем случае - O(n), в худшем случае – O(n2). Хоть и теоретически время сортировки совпадает с пузырьковой, однако в реальной работе, и с большими списками, сортировка шейкером показывает себя лучше.
4. Сортировка вставками реализует алгоритм перемещения нужного значения в начало списка, при полном прохождении списка. Данный метод сортировки обрабатывает элементы массива по порядку, все что находится слева от определенного индекса – уже отсортировано. Алгоритм в течение прохождения по списку, сравнивает второе значение с первым, если больше, ничего не делает, если меньше, производит так называемую вставку – вырезает элемент, весь, или часть списка сдвигаются вправо, и вырезанный элемент вставляется на нужное место. И крайнее значение отсортированного списка будет сравниваться с следующими значениями после него. Затрачиваемое время сортировки данных в лучшем случае – O(n) для сравнения, и O(1) для перестановок, а в худшем случае - O(n
2) для сравнений и перестановок. Отличие данного метода сортировки от предыдущих заключается в том, что для произведения вставки элементов, нужна дополнительно выделенная память.
5. Сортировка Шелла реализует усовершенствованный алгоритм вставками. Главным его отличием от сортировки вставками – сравнение элементов, стоящих не только рядом, но и на определенном расстоянии. Можно сказать, что это сортировка вставками с “грубыми” проходами, не требующими строгого задания шагов между элементами списка. Затрачиваемое время сортировки данных в лучшем случае - O(nlog2n), в худшем случае O(n2). Данный метод сортировки данных быстрее предыдущих, но медленнее быстрой сортировки, однако у нее есть и преимущества – отсутствие дополнительного потребления памяти, и даже при самых худших условиях, среднее время сортировки слабо изменяется.
6. Быстрая сортировка реализует совершенно иной алгоритм, с своими особенностями. Сначала из списка выбирается один элемент, который является опорным, другие элементы в списке распределяют и сортируют так, чтобы элементы меньше опорного оказались до него, а большие или такие же, после него. Затем, такой же алгоритм применяется рекурсивно для частей списка, находящихся слева и справа от опорного элемента. Такой метод сортировки списка значительно быстрее предыдущих, однако, зависит от выбора опорного элемента, при неправильном выборе, сортировка крайне медленна, и выполняется за O(n2) времени. Наилучшее же время сортировки – O(nlogn). Алгоритм отвечает типу – “разделяй и властвуй” (разделение списка на две части, и сортировка рекурсивно).
7. Сортировка слиянием реализует схожий принцип алгоритма быстрой сортировки. Происходит также деление списка на более мелкие части и сортировка их. Единственное отличие от быстрой сортировки – нет какого-либо опорного элемента, список делится пополам, и этот же процесс совершается рекурсивно для каждой части списка до тех пор, пока не будут отсортированы элементы, а затем эти же элементы будут вставлены обратно в верном порядке. Однако, у такого метода есть значительный минус – алгоритм выполняет все те же действия даже для частично отсортированного списка, что может повлиять на работу над такими списками. При таком раскладе, прочие методы сортировки справятся с списком значительно быстрее, чем сортировка слиянием. Сортировка слиянием использует тот же принцип, что и быстрая сортировка – “разделяй и властвуй”. Затрачиваемое время сортировки данных в лучшем случае – O(nlogn), в худшем случае все также – O(nlogn). Данный алгоритм довольно стабилен, однако он требует дополнительного выделения памяти под подсписки, которые возникают в процессе разделения и сортировки отдельных элементов, причем, процесс выделения памяти происходит постоянно, может произойти перевыделение памяти для списков.
8. Сортировка подсчетом реализует алгоритм с помощью подсчета, используется диапазон чисел сортируемого списка для подсчитывания количества совпадающих элементов. Такой метод применяется только в том случае, если значения подпадающие под алгоритм сортировки подсчетом, имеют сравнительно малый диапазон возможных значений по сравнению с сортируемым множеством. Как пример, сотни тысяч числовых значений, имеющих диапазон от 0 до 100. Обычные алгоритмы сортировки будут затрачивать в разы больше времени, чем сортировка подсчетом, которая каждое значение записывает в список отдельный, и так с каждым последующим значением. Однако, эта же сортировка крайне неэффективна для обычных списков, где диапазон значений схож с количеством их же.
9. Поразрядная сортировка реализует алгоритм сортировки целых числовых значений. Однако, такой алгоритм можно применить и для любых объектов, запись которых возможна с помощью деления на разряды. К этим данным можно отнести цифры, строки с набором символов, произвольные значения в памяти, которые представлены набором байтов. Сравнение в таких алгоритмах происходит с помощью разрядов, то есть, поразрядно, сравниваются значения одного крайнего разряда, и по этому результату сравнения, элементы группируются. Затем, значения следующих разрядов, и соседнего сравниваются, и опять элементы сортируются по порядку. Таким образом, алгоритм проходит до конца, до последнего разряда и сортирует все элементы. Затрачиваемое время сортировки данных в худшем случае – O(w*n), где w – это количество бит, которые требуется для хранения ключа, формула расхода памяти также аналогична [3].
- 1 2 3
Методы поиска
Для работы со структурами данных, необходима реализация алгоритмов поиска, ведь в значительно крупных списках, поиск нужного элемента осложняется, поиск вручную может занять множество времени. Исследования по нахождению новых методов поиска продолжаются и по сей день. Каждый алгоритм имеет свои плюсы и минусы, рассмотрим поподробнее основные методы поиска:
1. Последовательный поиск.
2. Бинарный поиск.
3. Интерполяционный поиск.
1. Последовательный поиск называется также линейным, является самым простым методом поиска. Алгоритм его реализуется следующим образом – указатель наводится на начало списка, и идет последовательно по всему списку, пока не будет найден нужный элемент, затем указатель будет остановлен. Главным его недостатком является низкая скорость при больших размерах списка, время работы пропорционально количеству элементов в структурах данных. Данный метод используется только в списках небольшого размера [4].
2. Бинарный поиск реализует алгоритм деления пополам, а затем сравнения среднего значения первого и второго частей списка с искомым значением, и при ближайшем совпадении, выбирается нужная часть списка, и поиск продолжается по такому же принципу. В конце концов, будет найден искомый элемент, либо же нет. Такой метод значительно быстрее работает при реализации поиска по спискам большого размера [5].
3. Интерполяционный поиск реализует алгоритм интерполирования, который подобен бинарному, но вместо деления области поиска на две равные части, интерполяционный поиск работает в отсортированном массиве значений, и сравнивает искомое значение с средним значением в части массива, если искомое значение меньше или больше части массива, он его отсекает, и продолжает поиск с таким же принципом до тех пор, пока не будет найдено искомое значение. Особенностью такого поиска является отсекание значительно больших значений, чем искомое, или значительно меньших, что позволяет сэкономить время и ресурсы. Данный алгоритм поиска определяется формулой 1 [6].
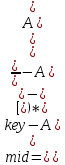 (1)
(1)2. Список очередь
Цель курсового проекта – реализация списка типа очереди, как типа данных, а также реализация функций работы с ним: добавление и удаление элементов, поиск, открытие из файла и сохранение в файл.
Для определения структуры в программном коде C++, используется функция struct. Пример реализации односвязной структуры данных в виде списка изображен на рисунке 4. В данной структуре название списка: “node”. А int data и node*next – компоненты структуры.

Рисунок 4 – Реализация структуры данных в виде списка
Целью курсовой работы является работа со списком типа очередь. Данный тип структуры данных представлен на рисунке 5 и работает по принципу FIFO – первый пришел, первый ушел.

Рисунок 5 – Список типа очереди
Добавление элементов в таких структурах данных происходит с конца списка, а удаление с начала. Очередь является динамической структурой, так как предполагает вставку и удаление элементов. Так как по заданию необходима реализация односвязного списка, то каждый элемент имеет только один указатель, на следующий элемент в списке, либо на конец.
2.1 Генерация очереди
Для генерации очереди и его элементов, была реализована функция Insert(), вставленная в цикл, зависящий от переменной int n, которая определяет размер списка, пример реализации генерации очереди представлен на рисунке 6.

Рисунок 6 – Генерация списка типа очереди
Переменная n задается пользователем, вводящим целочисленное значение с клавиатуры. В процессе генерации значений, используется функция rand(), которая производит случайную генерацию целочисленных значений, находящихся в промежутке от 0 до 99. Однако, эта же функция при повторных генерациях значений, берет те же самые значения из первой попытки генерации для правильной отладки разрабатываемой программы. Для полной рандомизации значений была использована функция srand(), которая при каждом запуске программы, генерирует совершенно новые случайные значения. Чтобы не менять каждый раз аргумент в функции srand(), используется функция time() в аргументах которой используется нулевой указатель - NULL, при выполнении time() с нулевым указателем, возвращается время системы, что обеспечивает полную рандомизацию значений при запуске программы. Реализация генерации случайных значений изображена на рисунке 7.