Файл: l_12.doc

Изохорический процесс

Изохорический процесс происходит при постоянном объеме. Зависимость давления от температуры описывается уравнением:

- закон Шарля , (2)

который читается: для данной массы газа при постоянном объеме давление газа линейно возрастает с увеличением температуры.

Изобарический процесс

Изобарический процесс. Это процесс, происходящий при постоянном давлении, Р=const.

Зависимость объема от температуры описывается законом:

- закон Гей-Люсака, (3)

который читается: для данной массы газа при постоянном давлении объем газа линейно возрастает с ростом температуры.

Адиабатический процесс

Адиабатическим процессом называется процесс, происходящий без теплообмена с окружающей средой (dQ = 0). Он описывается уравнением Пуассона:

, (4)

где  -постоянная адиабатического процесса. Постоянная адиабатического процесса равна:

. (5)

При адиабатическом процессе изменяются все параметры газа: давление, объем и температура.

2. Теплоемкость газа

Количество теплоты dQ , сообщенное телу при нагревании, равно

,

где с - удельная теплоемкость вещества, равная количеству теплоты, сообщаемой единице массы вещества для нагревания ее на один градус.

Помимо удельной теплоемкости вводится понятие мольной теплоемкости. Мольная теплоемкость С - равная количеству теплоты, сообщаемой одному молю вещества для нагревания его на один градус.

Мольная и удельная теплоемкости связаны между собой соотношением:

С = с, (6)

где С - мольная теплоемкость,  - молярная масса.

---

Газ можно нагревать при постоянном давлении и при постоянном объеме, поэтому для газа вводятся две теплоемкости: изобарическая и изохорическая. Мольная изобарическая и мольная изохорическая теплоемкости газа связаны с соответственными соотношениями:

; .

Отсюда видно, что отношение мольных теплоемкостей газа равно отношению удельных.

Количество теплоты, сообщенное 1 молю газа при изохорическом процессе, равно:

, (7)

а при изобарическом процессе

. (8)

3 Первое начало термодинамики

Количество теплоты dQ , сообщенное термодинамической системе, расходуется на увеличение ее внутренней энергии dU и на работу dA системы против внешних сил.

dQ = dU + dA . (9)

Внутренняя энергия U- суммарная энергия всех молекул в газе для идеального газа – кинетическая энергия вращательного и поступательного движения. Для одного моля газа определяется выражением

. (10)

Работа совершаемая газом равна

dA = pdV . (11)

где dV- изменение его объема.

Применение первого начало термодинамики Изотермический процесс

При этом процессе температура остается постоянной (Т=const) В этом случае dT=0 и внутренняя энергия не изменяется dU=0 dQ=dA, т.е. вся подводимая теплота расходуется газом на совершение работы против внешних сил.

Изохорический процесс

При изохорическом процессе V=const, dV=0 и dA=0. Т.е. при этом процессе работа не совершается, т.к. объем не изменяется. Тогда 1 начало запишется:

dQ = dU.

Т.е. количество теплоты расходуется на изменение внутренней энергии. Но по определению (для 1 моля). Следовательно,.

---

Из этой формулы видно, что изменение внутренней энергии газа определяется только изменением его температуры. Теплоемкость при постоянном объеме (изохорная теплоемкость) равна:

---

Изобарический процесс

В этом процессе изменяются и внутренняя энергия и работа против внешних сил:

,

т.е. теплота, подводимая к системе, идет на увеличение внутренней энергии и на совершение работы против внешних сил.

Для 1 моля газа уравнение Менделеева-Клапейрона

pV=RT ; pdV=RdT ,

но pdV=dA , поэтому dA=RdT , тогда

(Напомним, что С_ и C_p - мольные теплоемкости)

, (12)

R - универсальная газовая постоянная равная работе расширения одного моля газа при нагревании на один градус в изобарическом процессе.

Уравнение (12) называется уравнением Роберта Майера. Из него следует: при изобарном нагревании 1 моля газа на часть теплоты, равная, идет на увеличение внутренней энергии, а другая часть, равнаяR, - на совершение работы против внешних сил.

Адиабатический процесс

Так как при адиабатическом процессе dQ=0, то dA=-dU. Первое начало термодинамики будет иметь вид

dU+dA=0 или С_VdT+PdV=0

Откуда следует, что при адиабатическом процессе работа совершается за счет изменения внутренней энергии.

Например, если открыть ниппель у автомобильного колеса, то выходящий воздух можно рассматривать как адиабатическое расширение. Работа по расширению воздуха происходит за счет уменьшения внутренней энергии, что приведет к охлаждению воздуха и ниппель станет холодным.

Степени свободы

Согласно молекулярно-кинетической теории внутренняя энергия, которая обусловлена движением молекул как поступательным так и вращательным, определяется (6), где i- число степеней свободы

Числом степеней свободы i называется число независимых координат, полностью определяющих положение молекулы в пространстве.

---

В случае жесткой связи например:

1. У одноатомной молекулы только три степени свободы поступательного движения, i=3 (для атома как материальной точки не учитывается вращательное движение); (рис.1).

2. У двухатомной молекулы три степени свободы поступательного движения и две степени свободы вращательного движения, i=5 (рис.2);

3. У трехатомной молекулы три степени свободы поступательного движения и три степени свободы вращательного движения; i=6 (рис. 3).

Из (6) и (8) можно вычислить внутреннюю энергию и теплоемкости газа, а по формуле (1) определить адиабатическую постоянную .

1. Для одноатомного газа i=3

;

;

.

Адиабатическая постоянная .

2. Для двухатомного газа i=5 и аналогично предыдущему получим

3. Для трехатомного газа i=6

;

В общем случае:

; ; .

4.Теория метода и описание установки

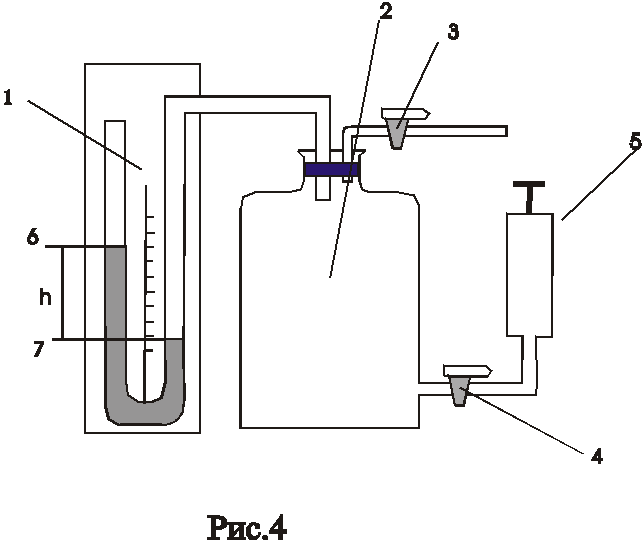
Рис.4.

Э

Рис.5.

кспериментальная установка состоит из стеклянного баллона2 (рис.4), соединенного с манометром 1 и насосом 5. Посредством крана 3 баллон 2 может быть соединен с атмосферой. Давление в манометре h определяется по разности уровней жидкости левого колена 6 и правого колена 7. Для накачки воздуха в баллон надо открыть кран 4 и закрыть кран 3.Если при помощи насоса накачать в баллон некоторое количество воздуха, а затем закрыть кран 4, то давление и температура воздуха внутри баллона повысятся(внешними силами совершается работа по сжатию газа). Выждав определенное время (2-3 мин), вследствие теплообмена воздуха с окружающей средой температура воздуха, находящегося в баллоне, сравняется с комнатной температурой , а давление при этом слегка понизится, о чем можно судить по показанию манометра.

---