§ 36. Уравнения линии. Задача о пересечении

трёх поверхностей.

Линия в пространстве определяется совместным заданием двух урав­нений

как пересечение двух поверхностей F(х, у, z) = 0 и Ф(x, у, z) = 0. Если F(x, у, z) = 0, Ф(х, у, z)==0, Ψ(х, у, z) = 0 суть уравнения трёх поверх­ностей, то для разыскания точек их пересечения нужно совместно решить систему:

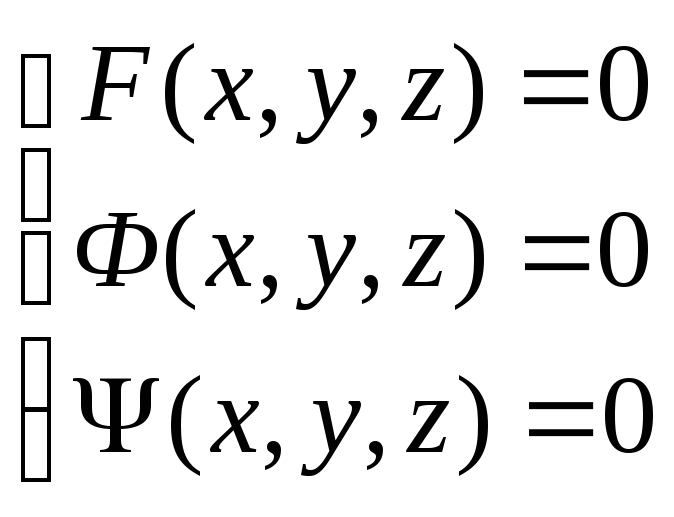
Каждое решение х, у, z этой системы представляет собой координаты одной из точек пересечения данных поверхностей.

900. Даны точки M₁(3; 4; —4), M₂(—3; 2; 4), М₃(— 1— 4; 4) и M₄(2; 3; —3). Определить, какие из них лежат на линии

и какие не лежат на ней.

901. Определить, какие из следующих линий проходят через начало координат:

1) 2)

3)

902. На линии найти точку:

1) абсцисса которой равна 3; 2) ордината которой равна 2; 3) апликата которой равна 8.

903. Установить, какие линии определяются следующими урав­нениями:

1) 2) 3) 4) 5)

6) 7) 8) 9)

---

10) 11)

904. Составить уравнения линии пересечения плоскости Oxz и сферы с центром в начале координат и радиусом, равным 3.

905. Составить уравнения линии пересечения сферы, центр ко­торой находится в начале координат и радиус равен 5, с плоско­стью, параллельной плоскости Охz и лежащей в левом полупро­странстве на расстоянии двух единиц от неб.

906. Составить уравнения линии пересечения плоскости Oyz и сферы, центр которой находится в точке С(5; —2; 1) и радиус равен 13.

907. Составить уравнения линии пересечения двух сфер, одна из которых имеет радиус, равный 6, и центр в начале координат, дру­гая имеет радиус, равный 5, и центр С(1; —2; 2).

908. Найти точки пересечения трех поверхностей:

х² +y²+x^{2 =}49, у — 3 = 0, z + 6 = 0.

909. Найти точки пересечения трёх поверхностей:

х² +y²+x^{2 =}9, x²+y² +(z — 2)² = 5, y - 2 = 0.

---

Смотрите также файлы

• kletenik_35.doc

• kletenik_34.doc

• kletenik_33.doc

• kletenik_32.doc

• kletenik_31.doc