ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 19.07.2024
Просмотров: 20
Скачиваний: 0
§ 41. Уравнения прямой
Прямая как пересечение двух плоскостей определяется совместным заданием двух уравнений первой степени:
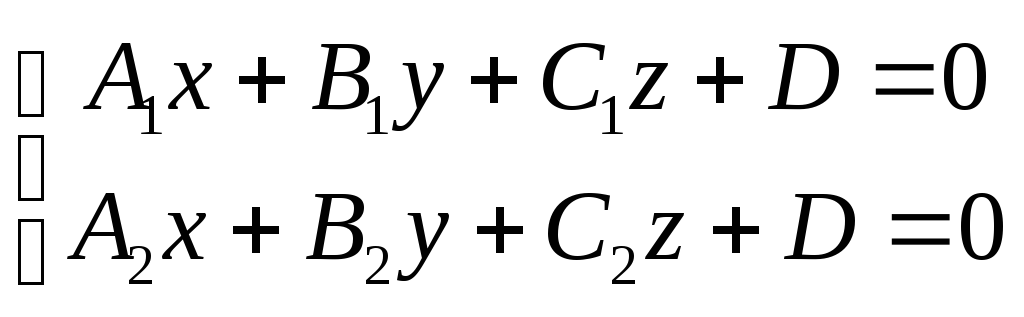
при условии, что коэффициенты A1, B1 C1 первого из них не пропорциональны коэффициентам A2, B2 C2 второго (в противном случае эти уравнения будут определять параллельные или слившиеся плоскости).
Пусть некоторая прямая а определена уравнениями (1) и α и β — какие угодно числа, одновременно не равные нулю; тогда уравнение
α (A1 x + B1y + C1z + D) + β (A2 x + B2y + C2 z + D) = 0 (2)
определяет плоскость, проходящую через прямую а.
Уравнением вида (2) (при соответствующем выборе чисел α, β) можно определить любую плоскость, проходящую через прямую а.
Совокупность всех плоскостей, проходящих через одну и ту же прямую, называется пучком плоскостей. Уравнение вида (2) называется уравнением пучка плоскостей.
Если α 0
то полагая
![]() ,
уравнение (2) можно привести к виду
,
уравнение (2) можно привести к виду
А 1 x + B1y + C1z + D1 + (А2 х + B2y + С2z + D 2) = 0. (3)
В таком виде уравнение пучка плоскостей более употребительно, чем уравнение (2), однако уравнением (3) можно определить все плоскости пучка, за исключением той, которой соответствует α = 0, т. е. за исключением плоскости
А 2 x + B2y + C2z + D2 = 0.
982. Составить уравнения прямых, образованных пересечением плоскости
5х — 7у + 2z — 3 = 0
с координатными плоскостями.
983. Составить уравнения прямой, образованной пересечением плоскости 3х — у - 7z + 9 = 0 с плоскостью, проходящей через ось Ох и точку E (3; 2; —5).
984. Найти точки пересечения прямой
![]()
с координатными плоскостями.
985. Доказать, что прямая
![]()
пересекает ось Оу.
986. Определить, при каком значении D прямая
![]()
пересекает: 1) ось Ох; 2) ось Оу; 3) ось Oz.
987. Найти соотношения, которым должны удовлетворять коэффициенты уравнений прямой
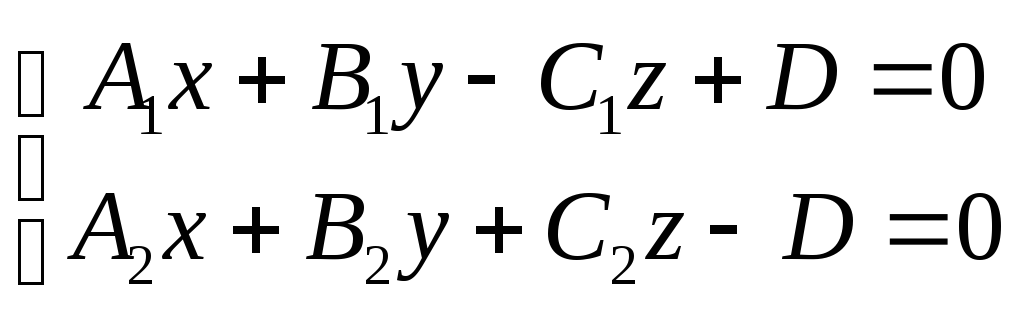
для того, чтобы эта прямая была параллельна: 1) оси Ох; 2) оси Оу; 3) оси Oz.
988. Найти соотношения, которым должны удовлетворять коэффициенты уравнений прямой
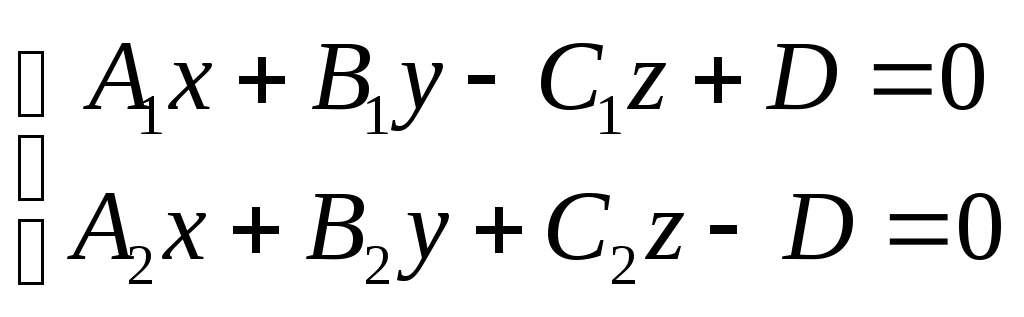
для того, чтобы эта прямая пересекала: 1) ось абсцисс; 2) ось ординат; 3) ось апликат; 4) совпадала с осью абсцисс; 5) совпадала с осью ординат; 6) совпадала с осью апликат.
989. В пучке плоскостей
2х— 3у + z — 3 + (х + 3у + 2z+1) = 0
найти плоскость, которая: 1) проходит через точку М1 (1;—2; 3); 2) параллельна оси Ох; 3) параллельна оси Оу; 4) параллельна оси Oz.
990. Составить уравнение плоскости, которая проходит через прямую пересечения плоскостей 3х — у + 2z + 9 = О, х + z — 3 = 0: 1) и через точку M1(4; —2; —3); 2) параллельно оси Ох; 3) параллельно оси Оу; 4) параллельно оси Oz.
991. Составить уравнение плоскости, проходящей через прямую пересечения плоскостей 2х—у + 3z — 5 = 0, х + 2у —z + 2 = 0 параллельно вектору l = {2; — 1; —2 }.
992. Составить уравнение плоскости, проходящей через прямую пересечения плоскостей 5х — 2у — z — 3 = 0, х + 3у — 2z + 5 = 0 параллельно вектору l = {7; 9; 17 }.
993. Составить уравнение плоскости, проходящей через прямую пересечения плоскостей 3х — 2у + z — 3 = 0, х— 2z = 0 перпендикулярно плоскости х — 2у + z + 5 = 0.
994. Составить уравнение плоскости, проходящей через прямую
![]()
перпендикулярно плоскости х + 19у — 7z— 11 =0.
995. Составить уравнение плоскости, которая проходит через прямую пересечения плоскостей 2х + у— z+1=0, х + у + 2z + 1 = 0 параллельно отрезку, ограниченному точками M1 (2; 5; — 3) 2), M2 (3; — 2; — 2).
996. Написать уравнение плоскости, принадлежащей пучку плоскостей
А 1 x + B1y + C1z + D1 + (А2 х + B2y + С2z + D 2) = 0.
и равноудалённой от точек M1(3; —4; —6), M2(1; 2; 2).
997. Определить, принадлежит ли плоскость
4х — 8у + 17z — 8 = 0
пучку плоскостей
α(5х — y + 4z— 1)+ β(2х + 2у — 3z + 2) = 0.
998. Определить, принадлежит ли плоскость
5х — 9у — 2z + 12 = 0
пучку плоскостей
α(2х — 3y + 4z—5) + β (х — 2у — z — 7) = 0.
999. Определить, при каких значениях l и т плоскость
5х + lу + 4z + т = 0
принадлежит пучку плоскостей
α(3х—7y +z—3) + β(х - 9у — 2z + 5) = 0.
1000. Написать уравнение плоскости, которая принадлежит пучку плоскостей
α(х—3y+7z +36) + β(2х + у —z —15) = 0.
и отстоит от начала координат на расстоянии р = 3.
1001. Написать уравнение плоскости, которая принадлежит пучку плоскостей
α(10х—8y — 15z + 56) + β(4х + у + 3z —1) = 0.
и отстоит от точки С(3; —2; —3) на расстоянии d = 7.
1002. Найти уравнение плоскости, которая принадлежит пучку плоскостей
α(4х+13y - 2z -60) + β(4х +3 у + 3z -30) = 0.
и отсекает от координатного угла Оху треугольник с площадью, равной 6 кв. ед.
1003. Составить уравнения плоскостей, проектирующих прямую —
![]()
на координатные плоскости.
1004. Составить уравнения проекций прямой
![]()
на координатные плоскости.
1005. Составить уравнение плоскости, проектирующей прямую
![]()
на плоскость х + 2у + 3z — 5 = 0.
1006. Составить уравнения проекции прямой
![]()
на плоскость 2х — у + 2— 1 = 0.