ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 20.07.2024
Просмотров: 15
Скачиваний: 0
ОТВЕТЫ (Глава 8)
885. Точки
M1,
M2,
M4,
лежат на поверхности,
точки М3,
М5,
М6
не лежат на ней.
Уравнение определяет сферу с центром
в начале координат и радиусом, равным
7. 886.
1) (1; 2; 2) и (1; 2; —2); 2) на данной поверхности
нет такой точки; 3) (2; 1; 2) и (2; — 1; 2); 4) на
данной поверхности нет такой точки.
887.
1) Плоскость Оуz;
2) плоскость Охz;
3) плоскость Оху;
4) плоскость, параллельная
плоскости Оуz
и лежащая в ближнем
полупространстве на расстоянии двух
единиц от неё; 5) плоскость, параллельная
плоскости Охz
и лежащая в левом
полупространстве на расстоянии двух
единиц от неё; 6) плоскость, параллельная
плоскости Оху и
лежащая в нижнем полупространстве на
расстоянии пяти единиц от неё; 7) сфера
с центром в начале координат и радиусом,
равным 5; 8) сфера с центром (2; —3; 5) и
радиусом, равным 7; 9) уравнение определяет
единственную точку — начало координат;
10) уравнение никакого геометрического
образа в пространстве не определяет;
11) плоскость, которая делит пополам
двугранный угол между плоскостями Охz,
Оуz
и проходит в 1, 3, 5 и 7
октантах; 12) плоскость, которая делит
пополам двугранный угол между плоскостями
Оху, Оуz
и проходит во 2, 3, 5 и
8 октантах; 13) плоскость, которая делит
пополам двугранный угол между плоскостями
Оху, Охz
и проходит в 1, 2, 7 и 8
октантах; 14) плоскости Охz
и Оуz;
15) плоскости Оху
и Оуz;
16) плоскости Оху
и Охz;
17) совокупность всех
трёх координатных плоскостей; 18) плоскость
Оуz
и плоскость, параллельная
плоскости Оуz
и лежащая а ближнем
полупространстве на расстоянии
четырёх единиц от неё; 19) плоскость Охz
и плоскость, которая
делит пополам двугранный угол между
плоскостями Охz,
Оуz
и проходит в 1, 3, 5 и 7
октантах; 20) плоскость Оху
и плоскость, которая
делит пополам двугранный угол между
плоскостями Оху, Охz
и проходит в 3, 4, 5 и 6
октантах. 889.
x2
+ y2
+ z2
= r2
890.
(х
— α)2
+ (у —
β)2
+ (z
— γ)
2 = r2.
891.
у — 3
=0. 892.
2z
—7
= 0. 893.
2x
+ 3 = 0. 894.
20y
+ 53 = 0. 895.
х2
+ у2
+ z2
= a2.
396.
х2
+ у2
+ z2
= a2.
897.
х +
2z
= 0. 893.
![]() 899.
899.
![]() 900.
Точки M1,
M3
лежат на данной линии;
точки M2
M4
не лежат на ней.
901.
Линии 1) и 3) проходят через начало
координат. 902.
1) (3; 2; 6) и (3; —2; 6); 2) (3; 2; 6) и (—3; 2; 6); 3) на
данной линии нет такой точки. 903.
1) Ось апликат; 2) ось
ординат; 3) ось абсцисс; 4) прямая, проходящая
через точку (2; 0; 0) параллельно оси Оz;
5) прямая, проходящая через точку (—2; 3;
0) параллельно оси Оz;
6) прямая, проходящая
через точку
(5; 0; — 2) параллельно оси Оу;
7) прямая, проходящая
через точку (0; — 2; 5) параллельно оси Ох;
8) окружность, лежащая
на плоскости Оху с
центром в начале координат и радиусом,
равным 3; 9) окружность, лежащая на
плоскости Охz
с центром в начале
координат и радиусом, равным 7; 10)
окружность, лежащая на плоскости Oyz
с центром в начале
координат и радиусом, равным 5; 11)
окружность, лежащая на плоскости z
— 2 = 0 с центром в точке (0; 0; 2) и радиусом,
равным 4.
900.
Точки M1,
M3
лежат на данной линии;
точки M2
M4
не лежат на ней.
901.
Линии 1) и 3) проходят через начало
координат. 902.
1) (3; 2; 6) и (3; —2; 6); 2) (3; 2; 6) и (—3; 2; 6); 3) на
данной линии нет такой точки. 903.
1) Ось апликат; 2) ось
ординат; 3) ось абсцисс; 4) прямая, проходящая
через точку (2; 0; 0) параллельно оси Оz;
5) прямая, проходящая через точку (—2; 3;
0) параллельно оси Оz;
6) прямая, проходящая
через точку
(5; 0; — 2) параллельно оси Оу;
7) прямая, проходящая
через точку (0; — 2; 5) параллельно оси Ох;
8) окружность, лежащая
на плоскости Оху с
центром в начале координат и радиусом,
равным 3; 9) окружность, лежащая на
плоскости Охz
с центром в начале
координат и радиусом, равным 7; 10)
окружность, лежащая на плоскости Oyz
с центром в начале
координат и радиусом, равным 5; 11)
окружность, лежащая на плоскости z
— 2 = 0 с центром в точке (0; 0; 2) и радиусом,
равным 4.
904.
![]() 905.
905.
![]()
906.
![]() 907.
907.
![]()
909. (1; 2;
2), (—1; 2; 2). 910.
1) Цилиндрическая поверхность с
образующими, параллельными оси Оу,
имеющая направляющей
окружность, которая на плоскости Охz
определяется уравнением
x2
+ z2
= 25; 2) цилиндрическая поверхность с
образующими, параллельными оси Ох,
имеющая направляющей
эллипс, который на плоскости Oyz
определяется уравнением
![]() ;
3) цилиндрическая поверхность с
образующими, параллельными оси Oz,
имеющая направляющей
гиперболу, которая на плоскости Оху
определяется
уравнением
;
3) цилиндрическая поверхность с
образующими, параллельными оси Oz,
имеющая направляющей
гиперболу, которая на плоскости Оху
определяется
уравнением
![]() 4) цилиндрическая поверхность с
образующими, параллельными оси Оу,
имеющая направляющей
параболу, которая на плоскости Охг
определяется уравнением
х* =
6z;
5) цилиндрическая поверхность с
образующими, параллельными оси Oz,
имеющая направляющей
пару прямых, которые на плоскости
Оху определяются
уравнениями х = 0, х —
у = 0; эта цилиндрическая
поверхность состоит из двух плоскостей;
6) цилиндрическая поверхность с
образующими, параллельными оси Оу,
имеющая направляющей
пару прямых, которые на плоскости Охг
определяются
уравнениями х —
2 = 0, x +
2 = 0; эта цилиндрическая поверхность
состоит из двух плоскостей; 7) ось абсцисс;
8) уравнение никакого геометрического
образа в пространстве не определяет;
9) цилиндрическая поверхность с
образующими, параллельными оси Оу,
имеющая направляющей
окружность; направляющая на плоскости
Охг определяется
уравнением хг
+ (z
— 1)2 =
1; 10) цилиндрическая поверхность с
образующими, параллельными оси Ох;
направляющая на
плоскости Oyz
определяется уравнением
у2
+ (z
+
4) цилиндрическая поверхность с
образующими, параллельными оси Оу,
имеющая направляющей
параболу, которая на плоскости Охг
определяется уравнением
х* =
6z;
5) цилиндрическая поверхность с
образующими, параллельными оси Oz,
имеющая направляющей
пару прямых, которые на плоскости
Оху определяются
уравнениями х = 0, х —
у = 0; эта цилиндрическая
поверхность состоит из двух плоскостей;
6) цилиндрическая поверхность с
образующими, параллельными оси Оу,
имеющая направляющей
пару прямых, которые на плоскости Охг
определяются
уравнениями х —
2 = 0, x +
2 = 0; эта цилиндрическая поверхность
состоит из двух плоскостей; 7) ось абсцисс;
8) уравнение никакого геометрического
образа в пространстве не определяет;
9) цилиндрическая поверхность с
образующими, параллельными оси Оу,
имеющая направляющей
окружность; направляющая на плоскости
Охг определяется
уравнением хг
+ (z
— 1)2 =
1; 10) цилиндрическая поверхность с
образующими, параллельными оси Ох;
направляющая на
плоскости Oyz
определяется уравнением
у2
+ (z
+
![]() )2
=
)2
=
![]() .
911.
1) x2
+ 5у2
— 8у
— 12 = 0; 2) 4x2
+ 5a2
+ 4z
— 60 = 0; 3) 2у
— 2z
— 2 = 0. 912.
1)
.
911.
1) x2
+ 5у2
— 8у
— 12 = 0; 2) 4x2
+ 5a2
+ 4z
— 60 = 0; 3) 2у
— 2z
— 2 = 0. 912.
1)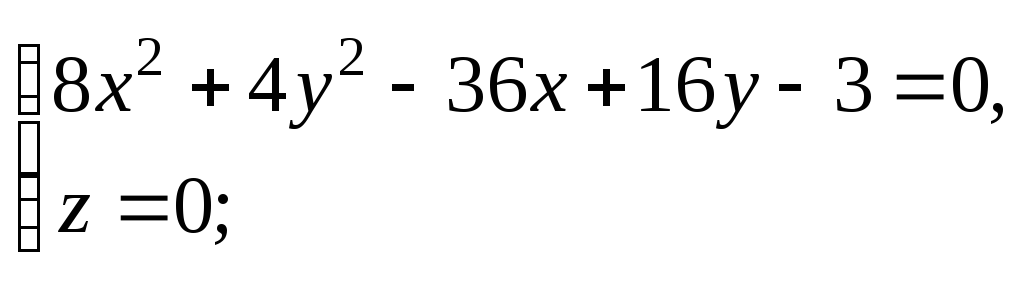 2)
2)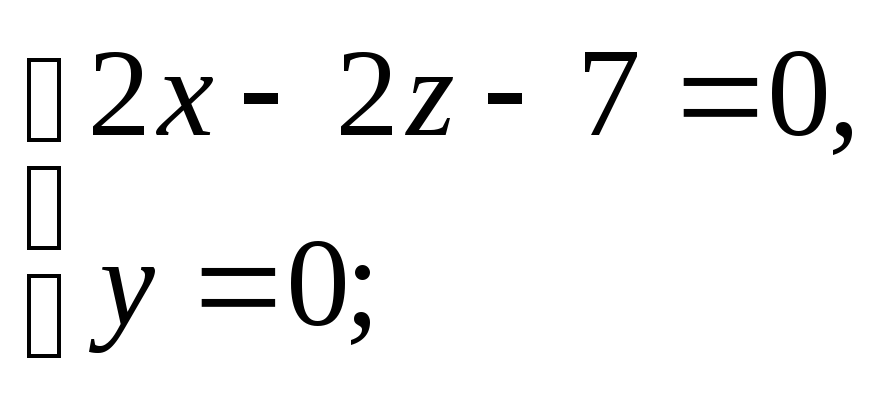 3)
3)