Файл: ЛабПр ТДиТМО.doc

При теплопроводности носителями тепловой энергии являются микрочастицы вещества – атомы и молекулы, при тепловом излучении – электромагнитные волны.

Конвекция– это способ переноса теплоты за счёт перемещения макроскопических количеств вещества из одной точки пространства в другую.

Таким образом, конвекция возможна только в средах, обладающих свойством текучести – газах и жидкостях. В теории теплообмена они обобщенно обозначаются термином «жидкость», не проводя различия, если это отдельно не требуется оговаривать, между капельными жидкостями и газами. Процесс переноса теплоты конвекцией, как правило, сопровождается теплопроводностью. Такой процесс называетсяконвективным теплообменом.

Конвективный теплообмен– это совместный процесс переноса теплоты конвекцией и теплопроводностью.

В инженерной практике чаще всего имеют дело с процессом конвективного теплообмена между поверхностью твердого тела (например, поверхность стенки печи, нагревательного прибора и т.п.) и текучей средой, омывающей эту поверхность. Этот процесс называется теплоотдачей.

Теплоотдача– частный случай конвективного теплообмена между поверхностью твердого тела (стенкой) и омывающей её текучей средой.

Различают вынужденную и свободную (естественную)конвекцию.

Вынужденная конвекцияпроисходит под действием сил давления, которые создаются принудительно, например насосом, вентилятором и т.п.

Свободная или естественная конвекцияпроисходит под действием массовых сил, имеющих различную природу: гравитационных, центробежных, электромагнитных и др.

На Земле свободная конвекция происходит в условиях действия силы тяжести, поэтому её называют тепловой гравитационной конвекцией. Движущей силой процесса в этом случае является подъёмная сила, которая возникает в среде при наличии неоднородности в распределении плотности внутри рассматриваемого объёма. При теплообмене такая неоднородность возникает за счет того, что отдельные элементы среды могут находиться при различной температуре. При этом более нагретые, а значит, менее плотные элементы среды под действием подъёмной силы будут перемещаться вверх, перенося вместе с собой теплоту, а более холодные, и значит, более плотные элементы среды будут перетекать на освободившееся место, как это показано на рис. 1.

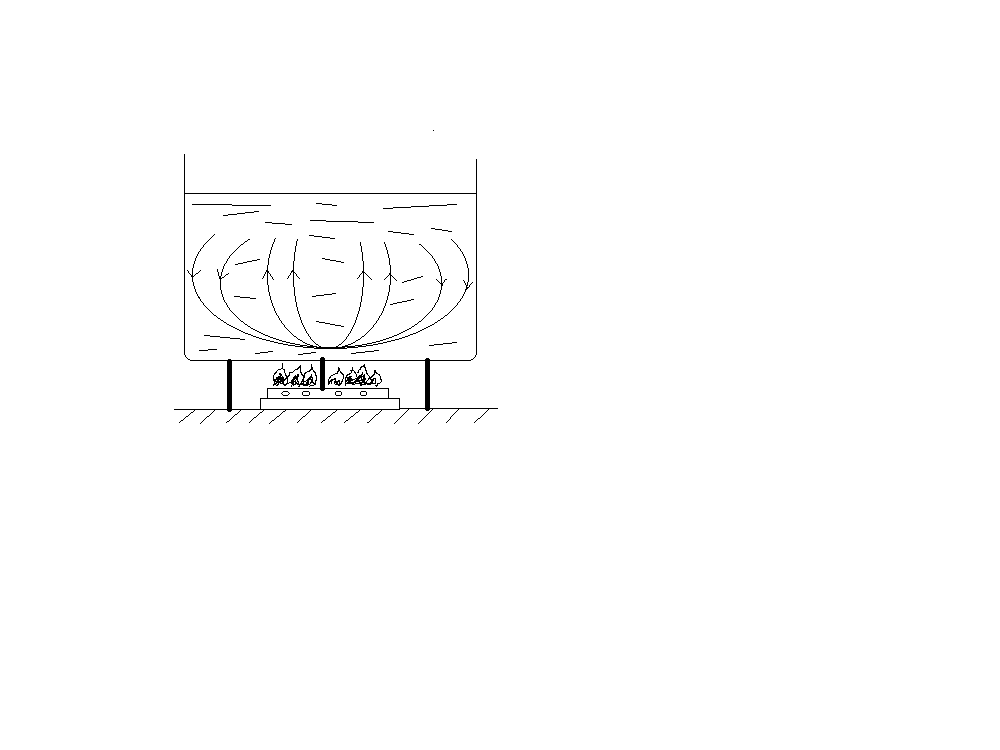
Рис. 1. Характер движения потоков в жидкости при свободной конвекции

Если в этом месте расположен постоянный источник теплоты, то при нагреве плотность нагреваемых элементов среды уменьшится, и они также начнут всплывать вверх. Так, пока будет иметь место разность плотностей отдельных элементов среды, будет продолжаться их круговорот, т.е. будет продолжаться свободная конвекция. Свободная конвекция, происходящая в больших объёмах среды, где ничто не препятствует развитию конвективных потоков, называется свободной конвекцией в неограниченном пространстве. Свободная конвекция в неограниченном пространстве, например, имеет место при отоплении помещений, нагреве воды в водогрейных котлах и многих других случаях. Если развитию конвективных потоков препятствуют стенки каналов или прослоек, которые заполнены текучей средой, то процесс в этом случае называетсясвободной конвекцией в ограниченном пространстве. Такой процесс имеет место, например, при теплообмене внутри воздушных прослоек между оконными рамами.

Основной закон, описывающий процесс конвективного теплообмена, – закон Ньютона-Рихмана. В аналитической форме для стационарного температурного режима теплообмена он имеет следующий вид:

,

где - элементарное количество теплоты, отдаваемое за элементарный промежуток времениот элементарной поверхности площадью;

- температура стенки;

- температура жидкости;

- коэффициент теплоотдачи.

Коэффициент теплоотдачипоказывает какое количество теплоты отдается в единицу времени от единицы поверхности при разности температур между стенкой и жидкостью в один градус. Единица измерения коэффициента теплоотдачи в системе СИ – Вт/м²∙град. При установившемся стационарном процессе коэффициент теплоотдачи можно определить из выражения:

, Вт/м²∙град

где - тепловой поток, Вт;

- площадь поверхности теплообмена, м²;

- температурный напор между поверхностью и жидкостью, град.

Коэффициент теплоотдачи характеризует интенсивность теплообмена между стенкой и омывающей её жидкостью. По своему физическому характеру конвективный теплообмен является весьма сложным процессом. Коэффициент теплоотдачи зависит от очень большого количества разнообразных параметров – физических свойств жидкости, характера течения жидкости, скорости течения жидкости, размера и формы канала, а также множества других факторов. В связи с этим невозможно дать общую зависимость для нахождения коэффициента теплоотдачи теоретическим путем

Коэффициент теплоотдачи наиболее точно и надежно может быть определен экспериментальным путем на основе уравнения (2). Однако в инженерной практике при расчете процессов теплообмена в различных технических устройствах, как правило, не представляется возможным выполнить опытное определение значения коэффициента теплоотдачи в условиях реального натурного объекта по причине сложности и дороговизны постановки такого эксперимента. В этом случае для решения задачи определения на помощь приходиттеория подобия.

Основное практическое значение теории подобия заключается в том, что она позволяет обобщить результаты отдельного опыта, проведенного на модели в лабораторных условиях, на весь класс реальных процессов и объектов, подобных процессу, изученному на модели. Понятие подобия, хорошо известное в отношении геометрических фигур, может быть распространено и на любые физические процессы и явления.

Класс физических явлений– это совокупность явлений, которые могут быть описаны одной общей системой уравнений и имеющие одинаковую физическую природу.

Единичное явление– это часть класса физических явлений, отличающихся определенными условиями однозначности (геометрическими, физическими, начальными, граничными).

Подобные явления– группа явлений одного класса с одинаковыми условиями однозначности, кроме числовых значений величин, содержащихся в этих условиях.

Теория подобия основана на том, что размерные физические величины, характеризующие явление, можно объединить в безразмерные комплексы, причем так, что число этих комплексов будет меньше, чем число размерных величин. Полученные безразмерные комплексы называютсякритериями подобия. Критерии подобия имеют определенный физический смысл и отражают влияние не одной физической величины, а всей их совокупности, входящей в критерий, что существенно упрощает анализ изучаемого процесса. Сам процесс в этом случае можно представить в виде аналитической зависимостимежду критериями подобия, характеризующими его отдельные стороны. Такие зависимости называютсякритериальными уравнениями. Критерии подобия получили названия по именам ученых, которые внесли существенный вклад в развитие гидродинамики и теории теплообмена – Нуссельта, Прандтля, Грасгофа, Рейнольдса, Кирпичева и других.

Теория подобия базируется на 3-х теоремах подобия.

1-я теорема:

Подобные между собой явления имеют одинаковые критерии подобия.

Эта теорема показывает, что в опытах нужно измерять лишь те физические величины, которые содержатся в критериях подобия.

2-я теорема:

Исходные математические уравнения, характеризующие данное физическое явление, всегда могут быть представлены в виде зависимости между критериями подобия, характеризующими это явление.

Эти уравнения называются критериальными. Эта теорема показывает, что результаты опытов следует представлять в виде критериальных уравнений.

3-я теорема.

Подобны те явления, у которых критерии подобия, составленные из условий однозначности, равны.

Эта теорема определяет условие необходимое для установления физического подобия. Критерии подобия, составленные из условий однозначности, называются определяющими. Они определяют равенство всех остальных илиопределяемыхкритериев подобия, что собственно является уже предметом 1-й теоремы подобия. Таким образом, 3-я теорема подобия развивает и углубляет 1-ю теорему.

При изучении конвективного теплообмена чаще всего используются следующие критерии подобия.

Критерий Рейнольдса (Re)– характеризует соотношение между силами инерции и силами вязкого трения, действующими в жидкости. Значение критерия Рейнольдса характеризует режим течения жидкости при вынужденной конвекции.

,

где - скорость движения жидкости;

- коэффициент кинематической вязкости жидкости;

- определяющий размер.

Критерий Грасгофа (Gr)– характеризует соотношение между силами вязкого трения и подъёмной силой, действующими в жидкости, при свободной конвекции. Значение критерия Грасгофа характеризует режим течения жидкости при свободной конвекции.

,

где - ускорение свободного падения;

- определяющий размер;

- температурный коэффициент объёмного расширения жидкости (для газов, где- определяющая температура по шкале Кельвина);

- температурный напор между стенкой и жидкостью;

- соответственно температура стенки и жидкости;

- коэффициент кинематической вязкости жидкости.

Критерий Нуссельта (Nu)– характеризует соотношение между количеством теплоты, передаваемой посредством теплопроводности и количеством теплоты, передаваемой посредством конвекции при конвективном теплообмене между поверхностью твердого тела (стенкой) и жидкостью, т.е. при теплоотдаче.

,

где - коэффициент теплоотдачи;

- определяющий размер;