ВУЗ: Пермский национальный исследовательский политехнический университет
Категория: Учебное пособие
Дисциплина: Информатика
Добавлен: 25.10.2018
Просмотров: 9573
Скачиваний: 96
131
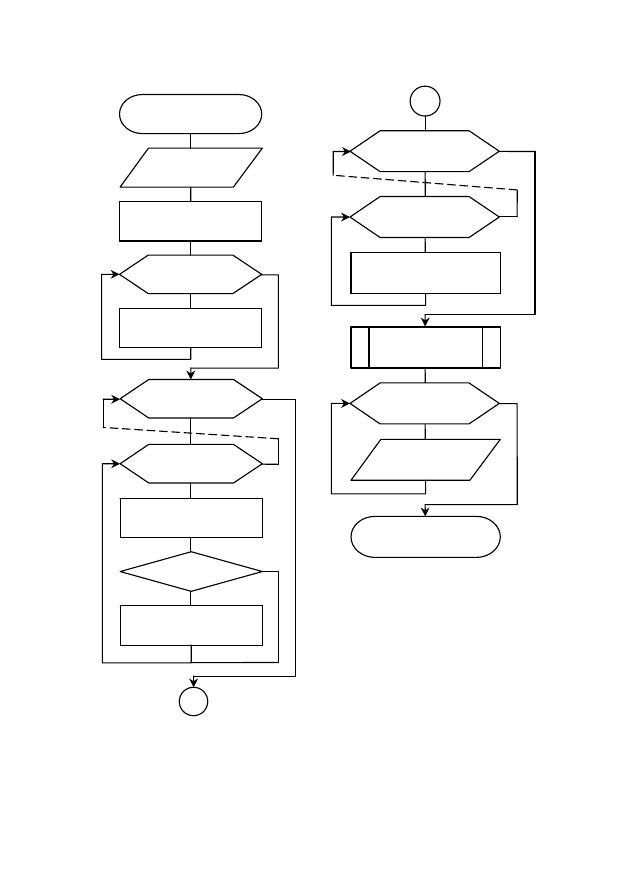
Рис. 29. Блок-схема алгоритма аппроксимации табличных
зависимостей многочленом степени m для n точек методом
наименьших квадратов
1
i = 1, m + 1
j = 1, m + 1
k = i + j – 1
a
ij
= w
k
Метод Гаусса
i = 1, m + 1
Вывод
a
i–1
=
, b
i
Конец
Начало
Ввод n, m,
x(n), y(n)
w
1
= n
i = 1, n
b
1
= b
1
+ y
i
i = 2, 2m+1
k = 1, n
w
i
= w
i
+ x
k
i–1
i
m + 1
b
i
= b
i
+ y
k
x
k
i–1
нет
да
1

132
массив w – вектор с количеством элементов, равным 2
1
m
. Кроме
этого, в блок-схеме использованы следующие обозначения: векто-
ры x и y – исходные табличные данные; n – количество точек таб-
лицы; m – степень многочлена (аппроксимирующей функции); b
i
–
вектор свободных членов. В результате выполнения приведенного
на рис. 29 алгоритма получаем: a
0
= b
1
, a
1
= b
2
, …, a
m
= b
m+1
.
Численные методы решения дифференциальных урав-
нений
Моделирование самых разнообразных процессов, разработ-
ка и исследование новых систем автоматического управления
различными объектами и многие другие проблемы связаны
с необходимостью численного решения дифференциальных
уравнений и их систем.
Уравнение, связывающее искомую функцию одной или не-
скольких переменных, эти переменные и производные различ-
ных порядков данной функции, называется дифференциальным
уравнением. Например, дифференциальными уравнениями будут
6 ,
10 3
y
x
y
x
.
В общем случае дифференциальное уравнение можно запи-
сать в виде
( , , , ,
) 0
n
G x y y
y
,
где G – некоторая функция от n + 2 переменных, при этом поря-
док n старшей производной, входящей в запись уравнения, на-
зывается порядком дифференциального уравнения.
Решением дифференциального уравнения называется такая
функция
( )
y
y x
, которая при подстановке ее в это уравнение
обращает его в тождество.
Задача о нахождении решения некоторого дифференциаль-
ного уравнения называется задачей интегрирования данного
дифференциального уравнения. График решения дифференци-
ального уравнения называется интегральной кривой. Без допол-
нительных предположений решение дифференциального урав-

133
нения принципиально неоднозначно, так как дифференциальное
уравнение задает семейство интегральных кривых на плоскости.
Для выделения однозначно определенной кривой (решения) не-
обходимо указать точку плоскости, через которую проходит ин-
тегральная кривая, и направление, в котором она проходит через
эту точку. Дополнительные условия такого рода называют на-
чальными, поскольку часто дифференциальные уравнения ис-
пользуются для описания динамических процессов – процессов,
проходящих во времени.
Математическое описание многих явлений часто сводится
к системе дифференциальных уравнений вида
1
1
1
2
2
2
1
2
1
2
, , ,...,
,
, , ,...,
,
...................................
, , ,...,
.
n
n
n
n
n
dy
f x y y
y
dx
dy
f x y y
y
dx
dy
f x y y
y
dx
(12)
Задача Коши для системы дифференциальных уравнений
(12) заключается в отыскании функций y
1
, y
2
, …, y
n
, удовлетво-
ряющих этой системе и начальным условиям
0
0
0
1
0
1
2
0
2
0
( )
,
( )
,
.................
( )
,
n
n
y x
y
y x
y
y x
y
где x – независимая переменная; y
1
(x), y
2
(x), …, y
n
(x) – неизвест-
ные (искомые) функции.
Существует возможность перехода от одной формы записи
к другой. Так, от записи в виде одного дифференциального
уравнения n-го порядка можно перейти к записи в виде системы
n дифференциальных уравнений 1-го порядка и наоборот.

134
Дифференциальное уравнение n-го порядка
( )
(
1)
( , , ,...,
)
n
n
y
f x y y
y
(13)
приводится к виду (12) с помощью замены (следующих преобра-
зований):
(
1)
0
1
2
1
,
,
, ...,
,
n
n
y
y
y
y
y
y
y
y
в результате получаем систему n дифференциальных уравнений
1-го порядка:
0
1
1
2
2
1
1
0
1
2
1
,
,
............
,
( , , , ,...,
).
n
n
n
n
dy
y
dx
dy
y
dx
dy
y
dx
dy
f x y y y
y
dx
(14)
Следовательно, решение дифференциального уравнения n-
го порядка сводится к решению системы n дифференциальных
уравнений 1-го порядка.
Например, дифференциальное уравнение 2-го порядка
2
5
x
y
y
y
xe
с помощью замены
0
1
,
y
y
y
y
приводит-
ся к системе дифференциальных уравнений 1-го порядка
0
1
1
0
1
,
5
2 .
x
dy
y
dx
dy
xe
y
y
dx
Методика численного решения дифференциального урав-
нения 1-го порядка на отрезке [x
0
, x
k
]
( )
( , )
dy
y x
f x y
dx
(15)

135
с начальными условиями
0
0
0
,
( )
x
y x
y
базируется на разложе-
нии искомой функции в ряд Тейлора в h-окрестности точки x
0
:
2
1
0
0
0
0
(
)
( )
( )
( ) ...
2!
h
y
y x
h
y x
h y x
y x
(16)
Численные методы решения дифференциальных уравнений
позволяют получить искомую функцию в виде таблицы ее при-
ближенных значений y
1
(x
1
), y
2
(x
2
), …, y
k
(x
k
).
Метод Эйлера
При отбрасывании всех членов ряда (16), содержащих про-
изводные 2-го и высших порядков, с учетом (15) получаем
1
0
0
0
0
(
)
( , )
y
y x
h
y
h f x y
,
где
0
0
( , )
f x y – правая часть дифференциального уравнения (15).
Пользуясь значением y
1
, получим значение искомой функ-
ции в следующей точке
2
1
x
x
h
:
2
1
1
1
1
(
)
( , )
y
y x
h
y
h f x y
.
Таким образом, если y
i
– приближенное значение искомой
функции в точке x
i
, тогда y
i+1
в следующей точке
1
i
i
x
x
h
на
каждом шаге интегрирования по методу Эйлера вычисляется по
формуле
1
( , )
i
i
i
i
y
y
h f x y
. (17)
Алгоритм решения дифференциального уравнения 1-го по-
рядка методом Эйлера представляет собой циклический процесс
вычислений искомой функции y по формуле (17) при изменении
аргумента x от x
0
до x
k
с шагом h.
Блок-схема алгоритма численного решения дифференци-
ального уравнения 1-го порядка вида (15) методом Эйлера при-
ведена на рис. 30.
Погрешность метода Эйлера
определяется отбрасываемой
частью разложения функции в ряд Тейлора (16),
= h
2
. Следова-