Файл: История развития средств вычислительной техники (Начало вычислений – ручной счёт).pdf

ВВЕДЕНИЕ

Сейчас, когда у каждого в кармане есть устройство (смартфон) по производительности превосходящее любую ЭВМ^[1] 50 лет назад, когда компьютер есть практически в каждом доме, а количество программ под эти типы устройств уже не поддаётся исчислению и перевалило за несколько миллионов^[2] не стоит забывать, что так было не всегда и их появление, и дальнейшее развитие было в первую очередь направлено на ускорение расчётов и автоматизацию процессов.

«..Ибо достойные люди недостойны терять часы, как рабы в вычислительном труде, который можно было бы безопасно отнести к кому-либо еще, если бы использовались машины»^[3] - Лейбниц, Готфрид Вильгельм.

В основном использованы англоязычные источники ввиду наибольшего вклада англоязычных авторов, ученых и изобретателей в развитие средств вычислительной техники. Использованы материалы национальных библиотек (Deutschen National Bibliothek, Biblioteca Nacional de Espana, Национальная библиотека им. Н. Э. Баумана), энциклопедий (Encyclopædia Britannica, Большая российская энциклопедия), музеев (Computer History Museum), университетов (University of St Andrews, MIT Libraries, Редакционно-издательский отдел Санкт-Петербургского государственного университета информационных технологий, механики и оптики), а так же электронные копии документов, рукописей и изданий размешенные на этих ресурсах, достоверность которых не может вызывать сомнений. А также в меньшей степени - книги и материалы с различных сайтов при использовании автором ссылок на проверенные источники.

1. Начало вычислений – ручной счёт

1.1 Пальцевый счёт

Самым первым, самым удобным способом расчётов при выполнении различных бытовых, обменных и торговых операций были пальцы рук. Пальцевый счёт, счёт на пальцах или дактилономия - математические вычисления, осуществляемые человеком с помощью сгибания, разгибания или указывания пальцев рук (иногда и ног). - древнейший способ счёта, используемый всеми известными народами. (Пал)

Частые наблюдения множеств, состоящих из пары предметов (глаза, уши, крылья, руки), привели человека к представлению о числе два. До сих пор слово "два" на некоторых языках звучит так же, как "глаза" или "крылья".

Если предметов было больше двух, то первобытный человек говорил «много». Лишь постепенно человек научился считать до трех, затем до пяти и до десяти и т.д. Название каждого числа отдельным словом было великим шагом вперед.

Для счета люди использовали пальцы рук, ног. Ведь и маленькие дети тоже учатся считать по пальцам. Однако этот способ годился только в пределах 20.

Известный русский путешественник Н. Миклухо-Маклай описал, как пользуются пальцевым счетом туземцы Новой Гвинеи — папуасы. Папуас загибает один за другим пальцы руки, повторяя: «бе, бе, ...». Загнув все пальцы, он говорит: «ибон-бе» (рука). Переходит на другую руку; загнув все пальцы, произносит: «ибон-али» (две руки). Далее переходит на ноги и поочередно говорит: «самба-бе» (одна нога), «самба-али» (две ноги). Если собственных рук и ног не хватает, папуас пользуется чужими конечностями.^[4]

Выход нашелся: считать на пальцах до 10, а затем начинать сначала, отдельно подсчитывая количество десятков. Система счисления на основе десяти возникла как естественное развитие пальцевого счета. При помощи пальцев рук люди научились не только считать большие числа, но и выполнять действия сложения и вычитания.

От пальцевого счета пошли пятеричная система счисления (одна рука), десятеричная (две руки), двадцатеричная (пальцы рук и ног).

Однако, пальцевый счет не был только примитивным загибанием пальцев. С помощью пальцев не только складывали и вычитали, но и умножали.

Существовали в разные времена разные системы пальцевого счета: единицами, парами (прямой и согнутый пальцы, что впоследствии стало основой программирования), тройками, четвёрками, пятками (одна рука), десятками (две руки), сороками (на суставах пальцев), шестидесятками (на фалангах пальцев).

Вековым традициям по использованию пальцевой двоичной системы счёта во многом должны быть обязаны современные инженеры. Именно она сподвигла их на создание современных электронных вычислительных машин и программ к ним.

При счете на пальцах в двоичной системе прямой палец может означать единицу, а согнутый - нуль. Тогда самое большое число, выраженное пальцами обеих рук, будет равно 1111111111, то есть 2¹⁰ – 1 = 1023 в десятичной системе, причем самая младшая единица соответствует мизинцу правой руки. «Два» в двоичной системе выражается как 10, то есть мизинец в согнутом состоянии, а безымянный палец прямой. Если еще выпрямить и мизинец, то это будет означать 11, то есть «три» в десятичной системе. Но при всех достоинствах пальцевого счёта в нём не хватало, как минимум, одного – записи или фиксации.

1.2 Фиксация счёта. Абак. Счёты

Фиксация результатов счета производилась различными способами: нанесение насечек, счетные палочки, узелки и др. Например, у народов доколумбовой Америки был весьма развит узелковый счет. Более того, система узелков выполняла также роль своего рода хроник и летописей, имея достаточно сложную структуру.

На смену древнему счету на пальцах пришёл счёт в абаке, который впервые появился, вероятно, в Древнем Вавилоне около 3 тыс. лет до н. э. Доска абака была разделена на полоски. Каждая полоска назначалась для откладывания тех или иных разрядов чисел: в первую полоску ставили столько камешков или бобов, сколько в числе единиц, во вторую полоску - сколько в нем десятков, в третью - сколько сотен, и так далее.

Один и тот же камешек на абаке мог означать и единицы, и десятки, и сотни, и тысячи - все дело лишь в том, на какой полоске он лежал. Чаще всего абаком пользовались для денежных расчетов. В Древней Греции бытовала шутка: "Придворный похож на камешек для абака: захочет счетчик, цена ему будет целый талант, а захочет - только хальк"^[5].

Наши счеты также представляют собой абак, состоящий из рамки с укрепленными горизонтальными веревочками, на которые были нанизаны просверленные сливовые или вишневые косточки (по 10 штук) (Рисунок 1 Абак и счёты).

А у китайцев на каждой проволоке не по десять шариков, а по семь. Последние два шарика отделены от первых, и каждый из них обозначает пять (так называемое «небо»). Когда при расчетах набирается пять шариков, вместо них откладывают один шарик второго отделения счетов. Такое устройство китайских счетов суан-пан уменьшает необходимое число шариков (Рисунок 1).

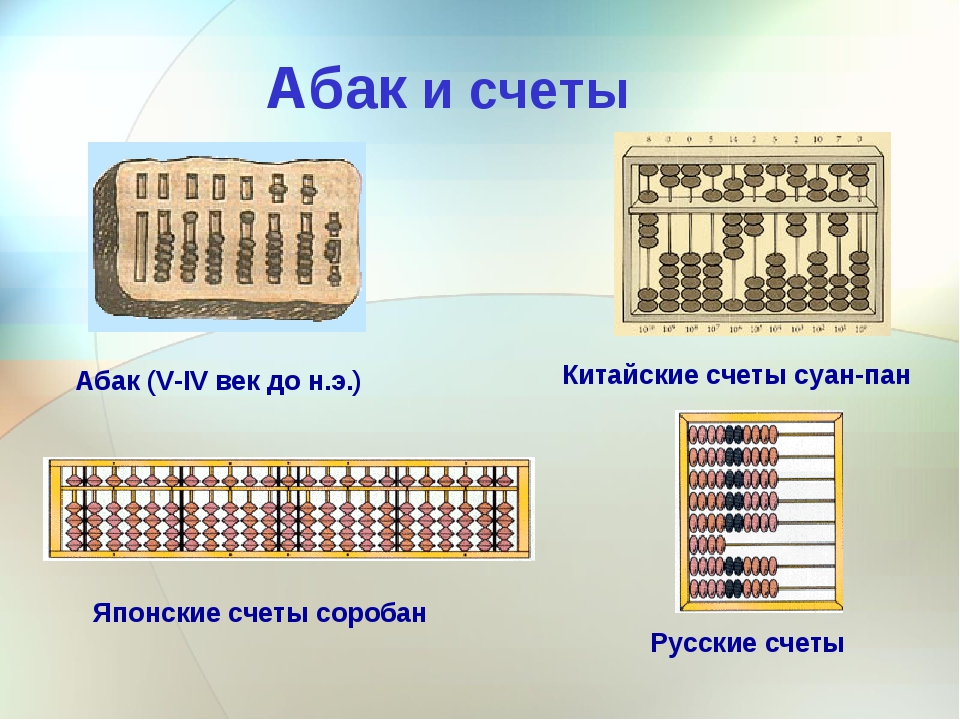У японцев это же устройство для счета носило название соробан. Соробан - японский абак, происходит от китайского суан-пана, который был завезен в Японию в XV - XVI веках. Соробан проще своего предшественника, у него на "небе" на один шарик меньше, чем у суан-пана^[6] (Рисунок 1).

Рисунок 1 Абак и счёты

Использование абака уже предполагает наличие некоторой позиционной системы счисления, например, десятичной, троичной, пятеричной и др.

1.3 Позиционная система счисления

При записи числа, в котором отсутствует какой-либо разряд (например, 101 или 1204), индийцы вместо названия цифры говорили слово «пусто». При записи на месте «пустого» разряда ставили точку, а позднее рисовали кружок. Такой кружок назывался «сунья» - на языке хинди это означало «пустое место». Арабские математики перевели это слово по смыслу на свой язык - они говорили «сифр». Современное слово «нуль» родилось сравнительно недавно - позднее, чем «цифра». Оно происходит от латинского слова «nihil» - «никакая».

Арабский ученый, математик Мухаммед бен Муса ал-Хорезми (из города Хорезма на реке Аму-Дарья) в своей книге подробно описал индийскую арифметику. Триста лет спустя (в 1120 году) эту книгу перевели на латинский язык, и она стала первым учебником «индийской» (то есть нашей современной) арифметики для всех европейских народов^[7].

Приблизительно в это же время индийские цифры начали применять и другие арабские учёные. Кроме того, ал-Хорезми приблизительно в 850 году н.э. написал книгу об общих правилах решения арифметических задач при помощи уравнений. Она называлась «Китаб ал-Джебр». Эта книга дала имя науке алгебре. Мухаммеду бен Муса ал-Хорезми мы обязаны появлению термина «алгоритм». В первой половине XII века книга ал-Хорезми в латинском переводе проникла в Европу. Переводчик, имя которого до нас не дошло, дал ей название Algoritmi de numero Indorum («Алгоритм о счёте индийском»).

2. Развитие и автоматизация средств вычислений

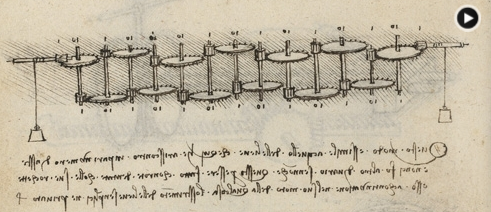Своего рода модификацию абака предложил Леонардо да Винчи (1452-1519) в конце XV - начале XVI века. Он создал эскиз 13-разрядного суммирующего устройства с десятизубными кольцами. Чертежи данного устройства были найдены среди двухтомного собрания Леонардо по механике, известного как "Codex Madrid"^[8]. Это устройство что-то вроде счетной машинки в основе которой находятся стержни, с одной стороны меньшее с другой большее, все стержни (всего 13) должны были располагаться таким образом, чтобы меньшее на одном стержне касалось большего на другом. Десять оборотов первого колеса должны были приводить к одному полному обороту второго, 10 второго к одному полному третьего и т.д. (Рисунок 2).

Рисунок 2 Многократный редуктор (трансформатор). Мадридский кодекс I (лист. 36)

Первая механическая машина была описана в 1623 г. профессором математики Тюбингенского университета Вильгельмом Шиккардом (Шиккард, Вильгельм (22.04.1592 - 24.10.1635))^[9], реализована в единственном экземпляре и предназначалась для выполнения четырех арифметических операций над 6-разрядными числами. Машина Шиккарда состояла из трех независимых устройств: суммирующего, множительного и записи чисел. Сложение производилось последовательным вводом слагаемых посредством наборных дисков, а вычитание - последовательным вводом уменьшаемого и вычитаемого. Вводимые числа и результат сложения/вычитания отображались в окошках считывания. Для выполнения операции умножения использовалась идея умножения решеткой. Третья часть машины использовалась для записи числа длиною более 6 разрядов.^[10]

2.1 Машина Паскаля^[11]

В машине французского математика, механика, физика, литератора и философа Блез Паскаля (Blaise Pascal 19.06.1623 – 19.08.1662) использовалась более сложная схема переноса старших разрядов, в дальнейшем редко используемая; но построенная в 1642 г. первая действующая модель машины, а затем серия из 50 машин способствовали достаточно широкой известности изобретения и формированию общественного мнения о возможности автоматизации умственного труда. Для выполнения арифметических операций Паскаль заменил поступательное перемещение костяшек в абаковидных инструментах на вращательное движение оси (колеса), так что в его машине сложению чисел соответствовало сложение пропорциональных им углов. Принцип действия счетчиков в машине Паскаля прост. В основе его лежит идея обыкновенной зубчатой пары - двух зубчатых колес, сцепленных между собой. Для каждого разряда имеется колесо (шестеренка) с десятью зубцами. При этом каждый из десяти зубцов представляет одну из цифр от 0 до 9. Такое колесо получило название "десятичное счетное колесо". С прибавлением в данном разряде каждой единицы счетное колесо поворачивается на один зубец, т. е. на одну десятую оборота. Требуемую цифру можно установить, поворачивая колесо до тех пор, пока зубец, представляющий эту цифру, не встанет против указателя или окошка. Например, три колеса показывают число 285. Мы можем прибавить к этому числу 111, повернув каждое колесо вправо на один зубец. Тогда против окошек встанут соответственно цифры 3, 9, 6, образуя сумму чисел 285 и 111, т. е. 396. Задача теперь в том, как осуществить перенос десятков. Это одна из основных проблем, которую пришлось решать Паскалю. Наличие такого механизма позволило бы вычислителю не тратить внимание на запоминание переноса из младшего разряда в старший. Машина, в которой сложение выполняется механически, должна сама определять, когда нужно производить перенос. Допустим, что мы ввели в разряд девять единиц. Счетное колесо повернется на 9/10 оборота. Если теперь прибавить еще одну единицу, колесо "накопит" уже десять единиц. Их надо передать в следующий разряд. Это и есть передача десятков. В машине Паскаля ее осуществляет удлиненный зуб. Он сцепляется с колесом десятков и поворачивает его на 1/10 оборота. В окошке счетчика десятков появится единица - один десяток, а в окошке счетчика единиц снова покажется нуль. Механизм переноса действует только в одном направлении вращения колес и не допускает выполнения операции вычитания вращением колес в обратную сторону. Поэтому Паскаль заменил операцию вычитания операцией сложения с десятичным дополнением. Пусть, например, необходимо из числа 285 вычесть 11. Метод дополнения приводит к действиям: 285-11=285-(100-89)=285+89-100=274. Нужно только не забывать вычесть 100. Но на машине, имеющей определенное число разрядов, об этом можно не заботиться. Вот как будет выполняться эта операция в шестиразрядной машине: 000285+999989=1000274; при этом единица слева выпадает, так как переносу из шестого разряда некуда деться. Машина Паскаля была практически первым суммирующим механизмом, построенным на совершенно новом принципе, при котором считают колеса. Она производила на современников огромное впечатление, о ней слагались легенды, ей посвящались поэмы. Все чаще с именем Паскаля появлялась характеристика "французский Архимед". (Пас)