Файл: Курсовая работа теплотехнический расчёт наружных ограждений здания.docx

Тогда для данной стены имеем
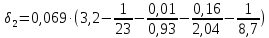=0,204 м
Принимаем δ₂ = 0,21 м и рассчитываем действительное сопротивление теплопередаче стены по формуле (2)
Rст= 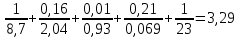(м²·°С)/Вт

1.3 Принятие сопротивлений теплопередачи, определение толщины теплоизоляционного слоя и расчет действительных сопротивлений теплопередаче перекрытия над неотапливаемым подвалом, имеющим световые проемы в стенах



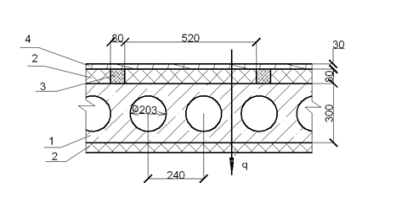
1-железобетон ρ=2500 кг/м³

2-плиты минераловатные жесткие на синтетическом связующем ρ=175 кг/м³

3-еловые лаги ρ=500 кг/м³

4-еловые доски ρ=500 кг/м³
Характеристики материалов перекрытия над неотапливаемым подвалом, имеющим световые проемы в стенах Таблица 4

Наименование материала	Плотность ρ, кг/м³	Расчётные коэффициенты при условиях эксплуатации Б
		теплопроводности λ, Вт/(м·°С)	теплоусвоения s, Вт/(м²·°С)	паропроницаемости µ, мг/(м·ч·Па)
Еловые доски	500	0,18	4,54	0,06
Железобетон	2500	2,04	19,70	0,03
Еловые лаги	500	0,18	4,54	0,06
плиты минераловатные жесткие на синтетическом связующем	175	0,069	1,08	0,45

Как видно, железобетонная плита является термически неоднородной конструкцией. Ввиду этого предварительно необходимо найти её приведённое термическое сопротивление. Расчёт проводится в следующей последовательности:

а) Выделяем характерное сечение (рис. 1, а).

Для облегчения расчётов заменим окружность равным по площади квадратом (исходя из соотношения Fокр = Fкв) со стороной:
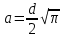(4)
и вычертим расчётное характерное сечение (рис. 1, б).

В нашем случае

---

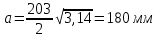
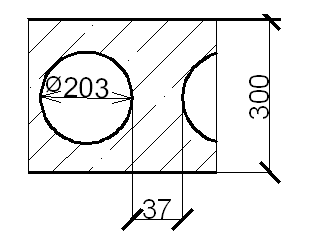
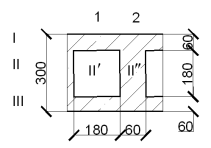
а б

Рис. 1. Характерное и расчётное сечение
б) Плоскостями, параллельными тепловому потоку, разбиваем на однородные зоны, которые могут быть однородными (из одного материала) и неоднородными, и вычисляем термическое сопротивление по формуле:
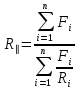, (5)

где F_i – площадь отдельных участков, м²;

R_i – термическое сопротивление данных участков, м²·°С/Вт:

– для однородных участков:
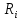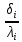= (6)
– для неоднородных участков:
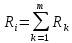(7)
Для приведённой конструкции: участок 1 – неоднородный, его сопротивление будет складываться из термического сопротивления железобетона суммарной толщиной δ₁ = 60 + 60 = 120 мм и термического сопротивления воздушной прослойки. Так как прослойка расположена со стороны помещения и перед утеплителем, то температура в ней будет положительной. Согласно табл. Б.1 [1] её термическое сопротивление будет равно Rв.п. = 0,15 м²·°С/Вт. В соответствии с формулой (6)
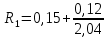=0, 209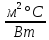
Участок 2 – однородный, его термическое сопротивление вычисляем по формуле (6):
R₂
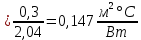
Термическое сопротивление параллельно тепловому потоку:


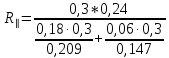
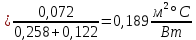
в) Плоскостями, перпендикулярными тепловому потоку, разбиваем на однородные зоны, которые могут быть однородными (из одного материала) и неоднородными. Термическое сопротивление однородных слоёв вычисляется по формуле (6), неоднородных – по формуле (5). Для приведённой конструкции

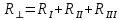
Очевидно, что термическое сопротивление слоёв I и III одинаково и равно

---

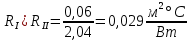
Слой II – неоднородный. Разобьём его на два участка: II´ – воздушная прослойка с сопротивлением R_II´ = 0,19 м²·°С/Вт, II´´ – железобетон с термическим сопротивлением
R_II”




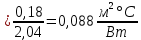
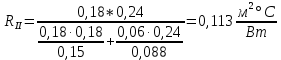
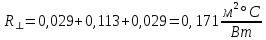
г) Проверим, превышает ли 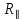на 25 % R⊥: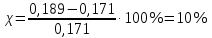

д) Так как 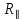не превышает R_⊥ на 25 %, то термическое сопротивление ограждения вычисляется по формуле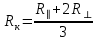



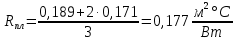
Так как конструкция утеплителя также неоднородна, то для нее находим термическое сопротивление

а) выделяем характерное сечение

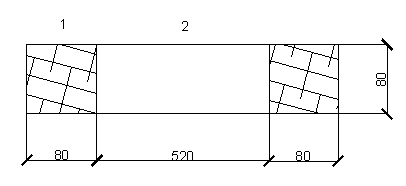
б) Плоскостями, параллельными тепловому потоку, разбиваем на однородные зоны, которые могут быть однородными (из одного материала) и неоднородными, и вычисляем термическое сопротивление по формуле (5)

– для однородных участков: (6)

– для неоднородных участков: (7)
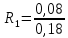=0, 44

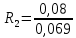=1, 159







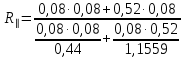
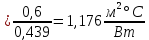
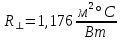
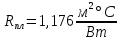
Из табл. 5.1 [1] RТ.НОРМ = 2,5 м²·°С/Вт.
n=0,75

=8,7 Вт/м²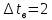°С

°С

---

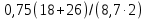= =1,89 м ²°С/Вт,
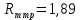так как =2,5 м²°С/Вт больше м²°С/Вт, то за расчетное принимаем большее сопротивление R₀=2,5 м²°С/Вт.

Принимаем согласно табл.5.7 [1] =12 Вт/м²°С.
=0, 0546 м
Принимаем δ2 = 0,055 м и рассчитываем действительное сопротивление теплопередаче стены по формуле (2)
R_п

---

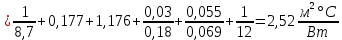
2. Расчёт минимальной температуры внутренней поверхности стены

Минимальная температура внутренней поверхности стены tв.п min, °С, определённая по формуле (8), не должна быть ниже температуры точки росы при расчётных значениях температуры и относительной влажности внутреннего воздуха:
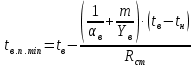(8)
где t_в, t_н и α_в – определённые в п. 2.2 величины;

t_н – расчётная зимняя температура воздуха, °С, принимаемая в зависимости от тепловой инерции стены;

m – коэффициент неравномерности теплоотдачи системы отопления, принимаемый по табл. 6.1 [1];

Yв – коэффициент теплоусвоения внутренней поверхности стены, Вт/(м²·°С), определяемый по пунктам 6.4 – 6.7 [1].

Определяем тепловую инерцию стены по формуле:
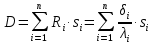(9)

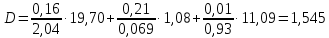+3,286+0,103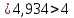
Так как D₁ = 1,545 > 1, то коэффициент теплоусвоения внутренней поверхности равен:
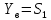(10)

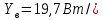м²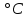

Так как D = 4,623 ∈ (4; 7], то в соответствии с табл. 5.2 [1] принимаем за расчетную cреднюю температуру наиболее холодных трех суток t³_н = –26°С.
= =0,84 м ²°С/Вт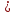
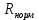
При центральном водяном отоплении m = 0,1.

---