Файл: Пифагор и его знаменитая теорема.docx

Все их можно разбить на малое число классов:

1. 
   Простейшее доказательство
   

Квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на его катетах.

Простейшее доказательство теоремы получается в случае равнобедренного прямоугольного треугольника. Вероятно, с него и начиналась теорема.

В самом деле, достаточно просто посмотреть на мозаику равнобедренных прямоугольных треугольников, чтобы убедиться в справедливости теоремы. Например, для ΔABC: квадрат, построенный на гипотенузе АС, содержит 4 исходных треугольника, а квадраты, построенные на катетах, -по два. Теорема доказана



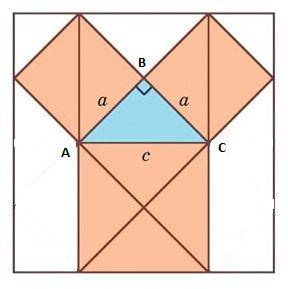
Рисунок 2 – Простейшее доказательство теоремы

2. 
   Метод подобия
   

Среди доказательств теоремы Пифагора алгебраическим методом первое место (возможно, самое древнее) занимает доказательство, использующее подобие.



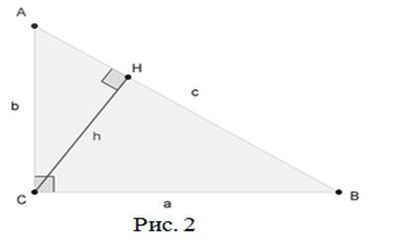
Рисунок 3 – Метод подобия

Пусть треугольник ABC - прямоугольный треугольник с прямым углом C. Проведём высоту из вершины C на гипотенузу AB, основание высоты обозначим как H.

Прямоугольный треугольник ACH подобен треугольнику ABC по двум углам (∠ACB=∠CHA=90%, ∠A- общий). Аналогично, треугольник CBH подобен ABC.

Введя обозначения: BC=a, AC=b, AB=c из подобия треугольников получаем, что a/c=H/B, b/c=A/H.

Отсюда имеем, что a2=c⋅HB,  b2=c⋅AH. Сложив полученные равенства, получаем:

a2+b2=c⋅HB+c⋅AH

a2+b2=c⋅(HB+AH)

a2+b2=c⋅AB

a2+b2=c⋅c

a2+b2=c2

Что и требовалось доказать.

3. 
   Доказательства методом площадей
   

Доказательства, несмотря на их кажущуюся простоту, вовсе не такие простые. Все они используют свойства площади, доказательства которых сложнее доказательства самой теоремы Пифагора.

(а+в)²=4*(ав/2)+с²;

а²+2ав+в²=2ав+с²;

или а²+ в²=с², что и требовалось доказать.



Рисунок 4 – Метод площадей

4. 
   Доказательство Евклида
   

Идея доказательства Евклида состоит в следующем: попробуем доказать, что половина площади квадрата, построенного на гипотенузе, равна сумме половин площадей квадратов, построенных на катетах, а тогда и площади большого и двух малых квадратов равны.

---

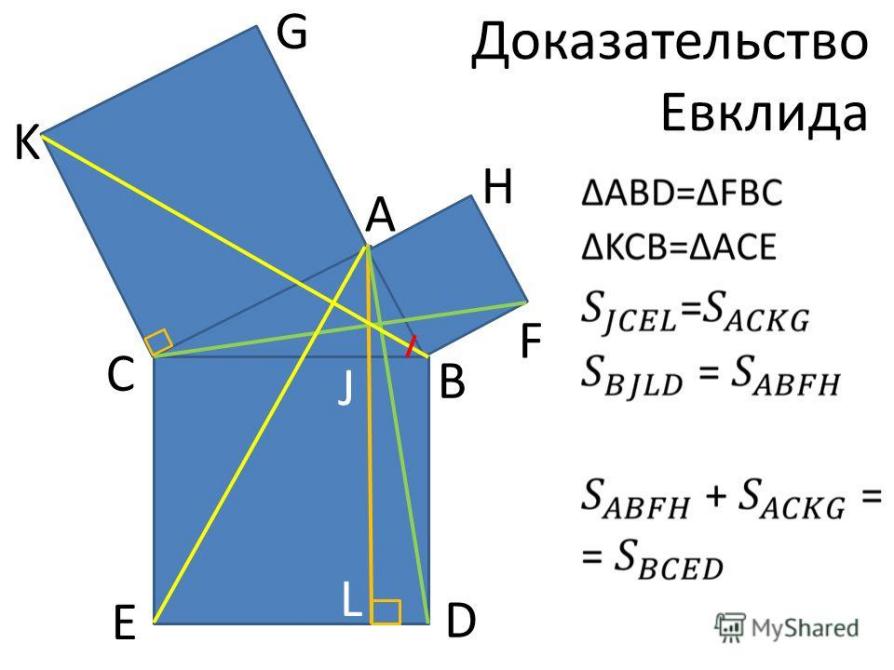
Рисунок 5 – Доказательство Евклида

2. Практическое применение теоремы Пифагора

   1. Применение теоремы в Вавилоне

В отличие от египтян, древние вавилоняне еще в середине II тысячелетия до н. э. хорошо знали, что сумма квадратов катетов равна квадрату гипотенузы. Сохранилась таблица, из которой ясно, что вавилонянам были известны многие «пифагоровы тройки» целых чисел, удовлетворяющих равенству х²+у²=z², в том числе совсем нетривиальные (например, 72, 65, 97 или 3456. 3367, 4825). К сожалению, мы ничего не знаем о том, каким методом были найдены эти числа.

Теорема Пифагора использовалась для вычисления диагонали квадрата; радиуса окружности, описанной около равностороннего треугольника: сторон правильных n - угольников. Сохранились и некоторые задачи, при решении которых надо воспользоваться этой теоремой: например, требовалось определить длину шеста, который вначале вертикально прислонен к стене, а затем наклоняется так, что его верхний конец опускается на три локтя, а нижний отходит от стены на 6 локтей.

В настоящее время всеобщее признание получило то, что успех развития многих областей науки и техники зависит от развития различных направлений математики. Важным условием повышения эффективности производства является широкое внедрение математических методов B технику народное хозяйство, что предполагает создание новых эффективных методов качественного и количественного исследования, которые позволяют решать задачи, выдвигаемые практикой.

2. Использование теоремы Пифагора в Древнем Египте

Древнегреческие авторы писали о существовании в Египте особого метода для построения прямого угла на местности: этому служила кольцевая веревка, на которой были отмечены 12 узелков на равных расстояниях. Если натянуть данную веревку, образовав треугольник со сторонами, пропорциональными 3, 4 и 5, то это треугольник будет прямоугольным: в самом деле, его стороны удовлетворяют теореме Пифагора (3² + 4²=5²).

Прямоугольные треугольники с целочисленными сторонами до сих пор иногда называются египетскими треугольниками. В то же время из сохранившихся древнеегипетских папирусов математического содержания невозможно извлечь никаких свидетельств о знакомстве с теоремой Пифагора, даже в ее частном случае. Вполне возможно, что египтяне знали только об одном целочисленном прямоугольном треугольнике, и знали о нем не раньше середины I тысячелетия до н. э. – времени, к которому относятся первые греческие сведения о египетском методе построения прямого угла.

---

Многие при имени Пифагор вспоминают его теорему. Но неужели мы можем встречать эту теорему только в геометрии? Нет, конечно, нет! Теорема Пифагора встречается в разных областях наук. Например: в физике, астрономии, архитектуре и в других.

3. Пример решения задачи

Задача №1 (арабского математика XI века).

На обоих берегах реки растет по пальме, одна против другой. Высота одной 30 локтей, другой - 20 локтей. Расстояние между их основаниями - 50 локтей. На верхушке каждой пальмы сидит птица. Внезапно обе птицы заметили рыбу, выплывшую к поверхности воды между пальмами. Они кинулись к ней разом и достигли её одновременно. На каком расстоянии от основания более высокой пальмы появилась рыба?



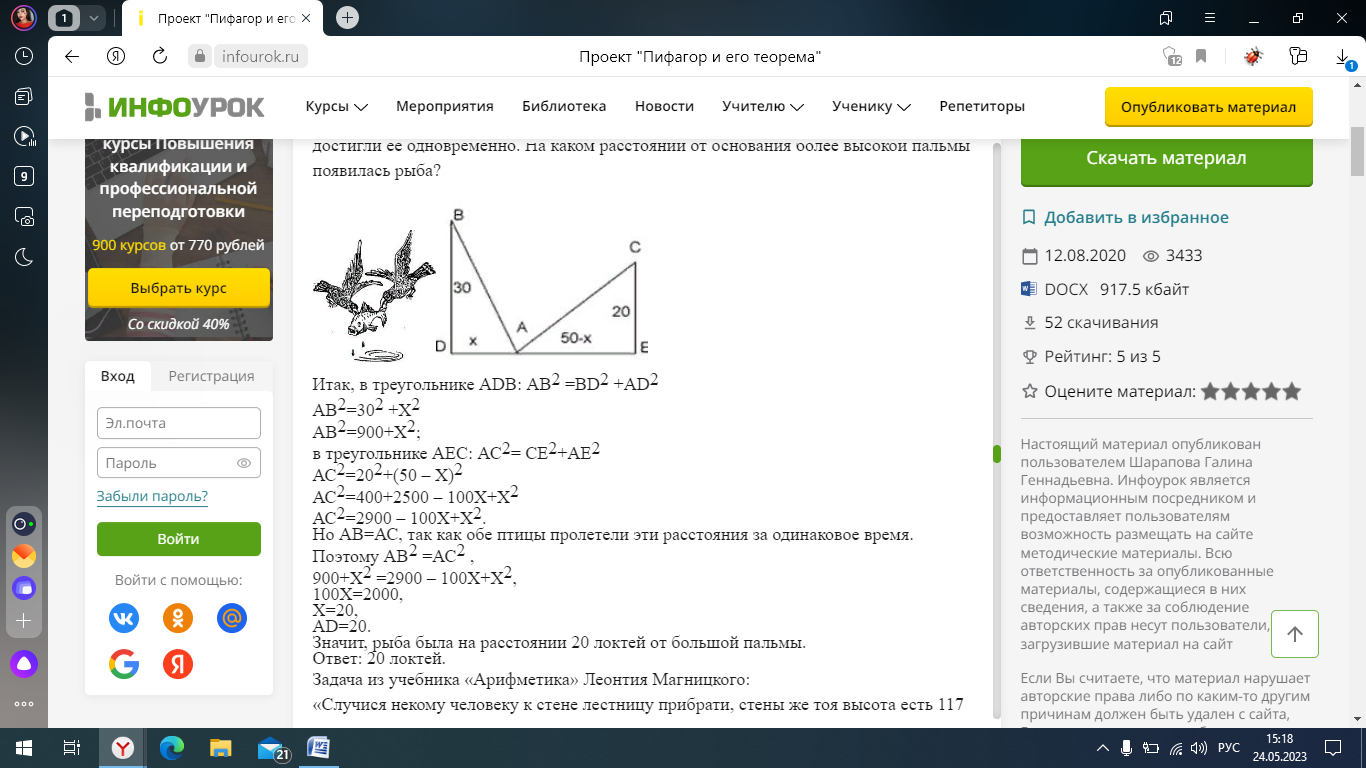
Рисунок 6 – К задаче №1
Итак, в треугольнике ADB: AB²=BD²+AD²

AB²=30²+x2

AB²=900+X²;

в треугольнике AEC: AC²=CE²+AE²

AC²=20²+(50-X²)

AC²=400+2500-100X+X²

AC²=2900-100X+X².

Но AB=AC, так как обе птицы пролетели эти расстояния за одинаковое время. Поэтому AB²=AC²,

900+X²=2900-100X+X²,

100X=2000,

X=20 →AD=20.

Значит, рыба была на расстоянии 20 локтей от большой пальмы.

Ответ: 20 локтей.

Успех развития многих областей науки и техники зависит от развития различных направлений математики. Важным условием повышения эффективности производства является широкое внедрение математических методов в технику и народное хозяйство, что предполагает создание новых, эффективных методов, которые позволяют решать задачи, выдвигаемые практикой.

Задача №2

Для разработки месторождения была установлена А-образная буровая вышка мачтового типа ВМА-45х200 высотой 45м и шириной основания 10м. Какова длина опоры вышки в м?



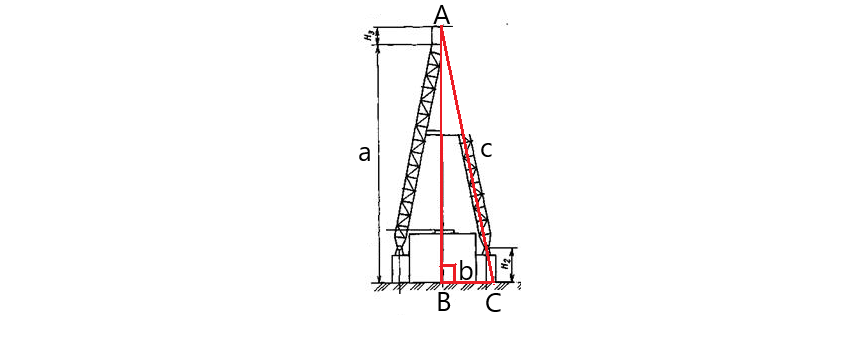
Рисунок 7 – К задаче №2
Итак, высота буровой вышки а=45м, половина ширины основания b=5м, нам необходимо найти длину опоры с. Зная теорему Пифагора, мы знаем, что прямоугольном треугольнике: а

---

²+в²=с².

Значит, с² = а²+в² => с²=45²+5²

с²=2025+25

с²=2050

с=45,3

Ответ: длина опоры вышки 45,3 м.

Заключение

Теорема Пифагора используется практически везде: в строительстве: для проектирования чертежа крыши дома, создания некоторых видов окон; в астрономии, в работе мобильной связи и в других вещах, которыми мы пользуемся ежедневно.

Теорема Пифагора - это одна из самых важных теорем геометрии. Значение её состоит в том, что из неё или с её помощью можно вывести большинство теорем геометрии. Теорема Пифагора была известна около 4000 лет назад, люди ещё находят новые способы её доказательства.

В целом, значение теоремы, кроме вышесказанного, заключается в том, что она применяется практически во всех современных технологиях, а также открывает простор для создания новых. Я считаю, что за теоремой Пифагора следует великое будущее многих открытий, которыми человечество потрясет весь мир.

Теорема Пифагора - фундамент, базис, основа всех математических вычислений, расчетов и многих изобретений. Проектная работа по изучению биографии Пифагора и математического наследия позволила в корне изменить все наши взгляды на этого великого и гениального ученого древности.

Список использованных источников

1. 
   Астахова В.Г.и др. «Мир вокруг нас», Москва, Издательство политической литературы,1983 год, 175с.
   
2. 
   Атанасян Л.С.и др. Геометрия 7-9.Учебник для общеобразовательных учреждений Москва «Просвещение», 2006 год
   
3. 
   Энциклопедический словарь юного математика Москва «Педагогика», 1989 год, 349с.
   
4. 
   Белл Э. Т. Творцы математики. Предшественники современной математики/ Под ред. С. Н. Киро. М., 1979
   
5. 
   5.Реньи А. Трилогия о математике (Диалоги о математике. Письма о вероятности. Дневник – Записки студента по теории информации)/ Пер. с венг. Под ред. Б. В. Гнеденко. М., 1980 10.
   
6. 
   Хрестоматия по истории математики в 2-х т./ Под ред. А. П. Юшкевича. М., 1975, 1976
   
7. 
   Математика в школе. Рубрики «Математический календарь» и «Ученые-математики» (с 1975 г.)
   
8. 
   http://moypifagor.narod.ru/
   

---