Файл: Вид работы Курсовая работа Название дисциплины Электрические и электронные аппараты Тема Электродинамические усилия, действующие в электрических аппаратах причины возникновения, характер и методика расчета.doc

откуда:

В тех случаях, когда приходится на практике определять электродинамическое усилие между частями или сторонами одного и того же контура с индуктивностью L1—L, сила взаимодействия будет составлять:


Таким образом, сделаем вывод, что для системы из нескольких обтекаемых током проводников можно всегда представить, что любой из этих проводников расположен в магнитном поле, созданном токами других проводников, и соответствующим образом взаимодействует с этим полем, т.е. между проводниками, охваченными общим магнитным потоком, всегда возникают механические силы. Эти силы называются электродинамическими.

Аналогичные силы возникают между проводником, обтекаемым током, и ферромагнитной массой. Направление действия силы определяется «правилом левой руки».



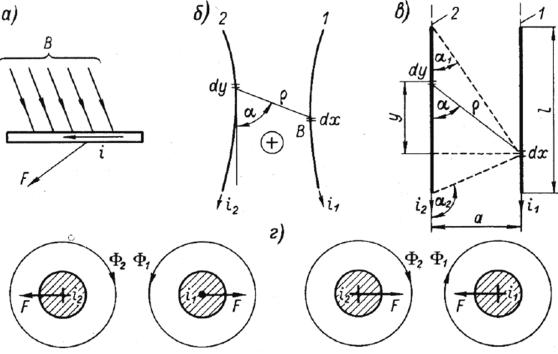
Рис.1. К определению электродинамической силы между двумя проводниками
Направление действия силы может быть также определено из следующего общего положения: силы, действующие в контуре с током, стремятся изменить конфигурацию контура так, чтобы охватываемый контуром магнитный поток увеличился.

В литературе, посвящённой электрическим аппаратам, электродинамические силы для краткости обозначаются сокращением ЭДУ (электродинамические усилия).

Весьма удобным для определения направления действия ЭДУ является метод, предложенный акад. В. Ф. Миткевичем, основанный на представлении бокового распора и тяжения магнитных линий. Рисуют и накладывают друг на друга картины магнитных полей, создаваемых током каждого из проводников. Благодаря боковому распору магнитных силовых линий сила, действующая на проводник, направлена в сторону, где поле ослаблено (рис. 1,г).

При нормальных эксплуатационных условиях ЭДУ, как правило, малы и не вызывают каких-либо деформаций, а тем более поломок деталей в аппаратах.

Однако при коротких замыканиях эти силы достигают весьма больших значений и могут вызвать деформацию или разрушение не только отдельных деталей, но и всего аппарата. Это обстоятельство требует проведения расчета аппарата (или отдельных его узлов) на электродинамическую устойчивость, т.е. на способность выдержать без повреждений прохождение наибольшего возможного в эксплуатационных условиях (или заданного) тока короткого замыкания (КЗ). Такой расчет тем более необходим ввиду того, что с целью получения минимальных габаритов в аппаратах стремятся располагать токоведущие части как можно ближе друг к другу.

---

2 Методика расчета электродинамических сил в электрических аппаратах

Расчет электродинамических сил ведется обычно либо на основании закона взаимодействия проводника с током и магнитным полем (первый метод), либо по изменению запаса магнитной энергии системы (второй метод).

Первый метод



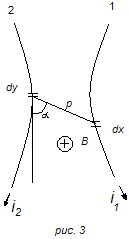
Рис. 1. Расчет электродинамических сил на основании закона взаимодействия проводника с током и магнитным полем.
Известно, что на элемент dl₁ проводника длиной l₁ с током i₁, расположенного в однородном магнитном поле с индукцией , действует механическая сила (сила Ампера).
, (1)
где - угол между направлением тока и вектором индукции.

Эту механическую силу называют электродинамической. Электродинамические силы возникают не только в контуре с током, расположенным во внешнем магнитном поле, но и в случае, когда этот контур уединен, и поле, его окружающее, определяется током в самом контуре.

При прохождении тока к. з., превышающего номинальный в 10–20 раз, на токоведущей контур электрического аппарата воздействуют значительные электродинамические силы, стремящиеся деформировать этот контур. При прохождении тока по соседним токоведущим контурам также возникают силы, которыми контуры взаимодействуют между собой. В сильноточных электрических аппаратах электродинамические силы могут достигать десятков тысяч ньютон. Способность электрического аппарата противостоять механическим нагрузкам, возникающих в токоведущих частях и поддерживающих их элементах в режиме к. з., называется электродинамической стойкостью.

Электродинамические силы зависят от наибольшего значения тока, от длины, конфигурации и взаимного расположения деталей, образующих токоведущий контур, а также от магнитных свойств окружающей среды. Токоведущие части могут располагаться как в среде с постоянной магнитной проницаемостью, не зависящей от напряженности магнитного поля (воздух, жидкие твердые изоляционные материалы), так и в среде, магнитная проницаемость которой зависит от напряженности магнитного поля.

Электродинамические силы определяются или с помощью закона Ампера (формула 3), или по изменению запаса магнитной энергии токоведущего контура. Первый метод рекомендуется применять тогда, когда можно аналитически найти индукцию в любой точке проводника, для которого необходимо определить силу. Индукцию определяют, используя закон Био-Савара-Лапласа, согласно которого элементарная индукция

---

dB от элемента dl₂ проводника l₂ с током i₂ в произвольной точке М, в нашем случае принадлежащей элементу dl₁ проводника l₁, равна:
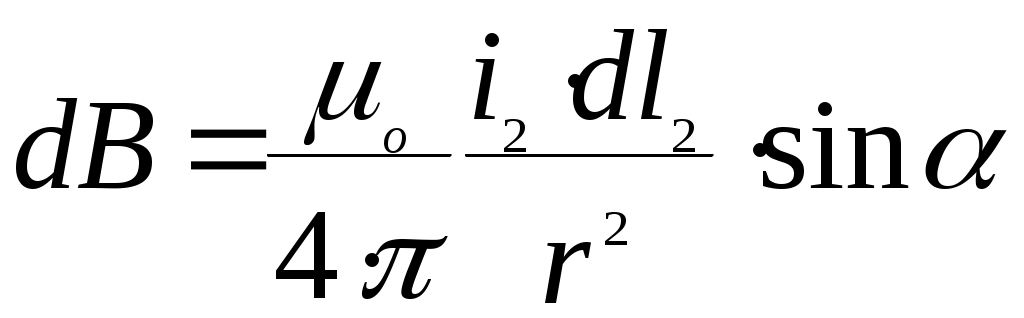, (2)
где -магнитная проницаемость вакуума равная 4 10^-7 Гн/м;

-угол между током i₂ и лучом r.

Индукция в точке М, создаваемая током, проходящим по всему проводнику l₂:
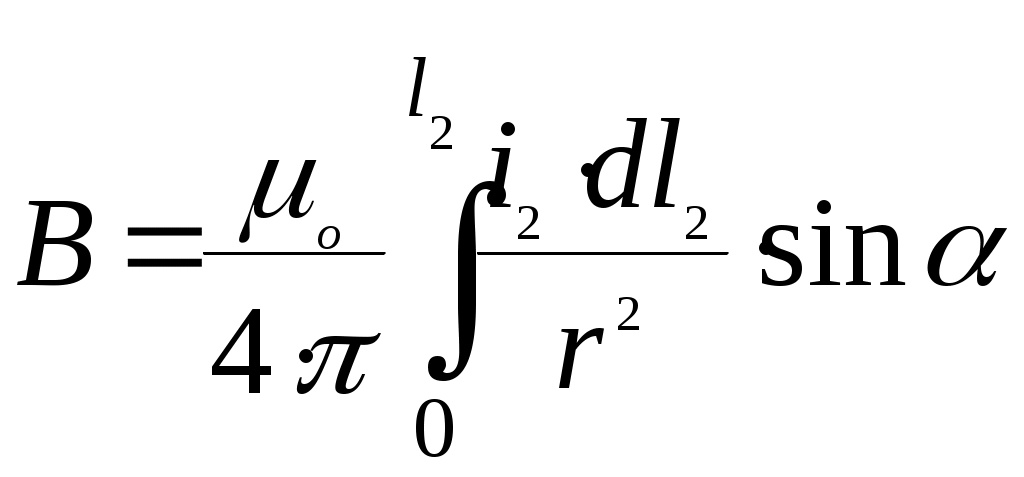(3)
Силу, действующую на весь проводник l₁, определим, подставив (3) в (1)
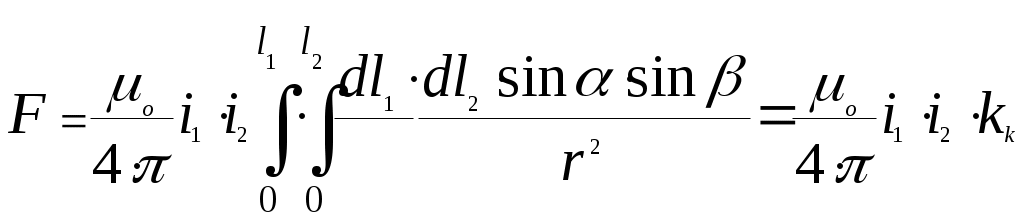, (4)
где k_k – коэффициент контура, величина интеграла, зависящая только от геометрических размеров проводников и их взаимного расположения.

Полученные формулы справедливы, когда можно считать, что токи протекают по осям проводников, а форма и размеры сечений проводников не влияют на электродинамические силы.

По формуле (4) определяется суммарная величина электродинамической силы взаимодействия данных проводников или контуров с токами, т.е. равнодействующая электродинамические сил. Точки приложения этой силы зависят от характера распределения электродинамические сил по длине проводников, обусловленного их конфигурацией и взаимным расположением.

Как уже сказано, при втором методе электродинамические силы определяются по изменению запаса магнитной энергии токоведущего контура. Электромагнитное поле вокруг проводников и контуров с током обладает определенным запасом энергии. Электромагнитная энергия контура с током i.
(5)
Электромагнитная энергия двух контуров, обтекаемых токами i₁ и i₂
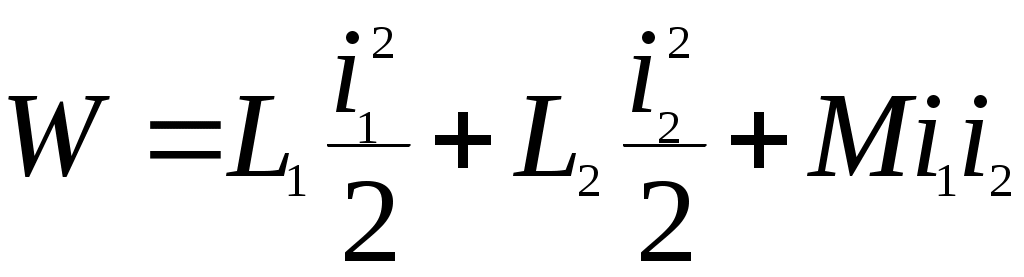, (6)
где L₁ и L₂- индуктивность контуров; М – взаимная индуктивность контуров.

Всякая деформация контура (изменение расположения его элементов или частей) или изменение взаиморасположения контуров приводят к изменению запаса электромагнитной энергии. При этом работа сил в любой системе равна изменению запаса энергии этой системы:

---

, (7)
здесь dW- изменение запаса энергии системы при деформации системы в направлении х под действием силы F.

На указанном законе и основан второй метод определения электродинамических сил в контурах. Электродинамическая сила в контуре иле между контурами, действующая в направлении х, равна скорости изменения запаса энергии системы при деформации ее в том же направлении:
(8)
Согласно сказанному электродинамическая сила в контуре, обтекаемом током i
, (9)
а электродинамическая сила между двумя взаимосвязанными контурами с токами i₁ и i₂
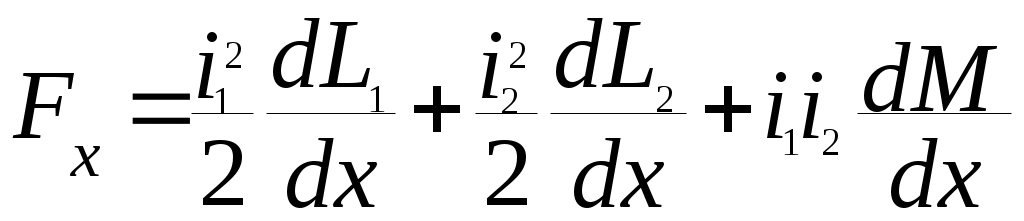(10)
Рассмотрим электродинамические силы в наиболее простых случаях взаимного расположения проводников как при допущении, что форма и размеры сечений проводников не влияют на электродинамические силы, а токи протекают по осям проводников, так и с учетом формы и размеров сечений.

Направление вектора силы Ампера определяется по правилу левой руки: вектор магнитной индукции входит в ладонь, четыре пальца направлены вдоль тока, большой отогнутый палец покажет направление вектора силы. При этом направление вектора магнитной индукции определяется следующим образом. Если смотреть вдоль проводника по направлению тока, то вектор магнитной индукции направлен по ходу часовой стрелки.

Модуль электродинамические силы определяются или с помощью закона Ампера, или по изменению запаса магнитной энергии токоведущего контура.

1. 
   Электродинамические силы между параллельными проводниками бесконечной длины
   

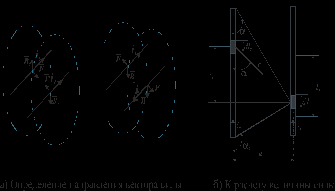
Рис.2. Определение направления электродинамических сил между параллельными проводниками бесконечной длины

Если токи в параллельных проводниках направлены одинаково, то векторы силы направлены навстречу друг другу – проводники испытывают взаимное притяжение. Если токи в параллельных проводниках направлены противоположно, то наоборот – проводники отталкиваются.

---

И для искомой электродинамической силы, действующей на участок l₁ проводника с током i₁ можно записать
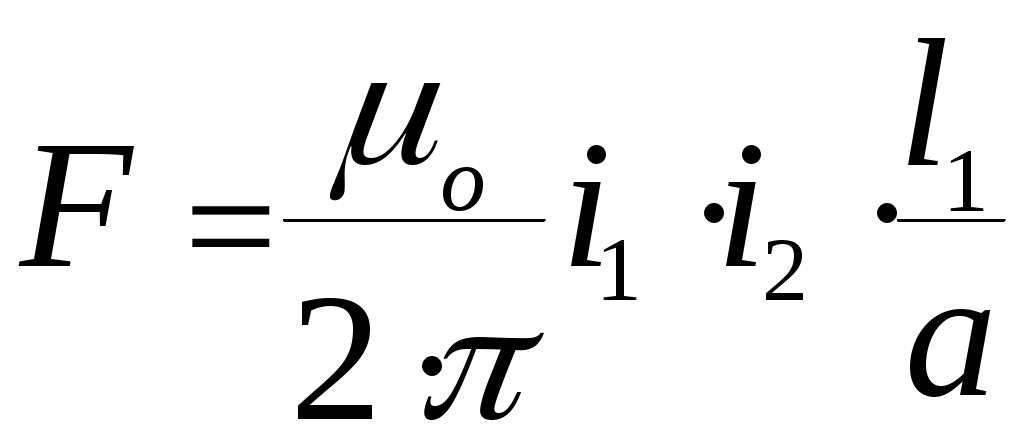(11)
где – расстояние между проводниками.

Электродинамические силы между проводниками, расположенными под прямым углом.



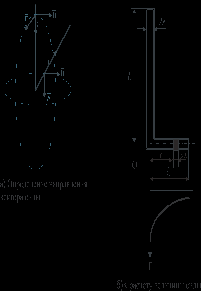
Рис.3. Определение направления электродинамические сил между проводниками, расположенными под прямым углом
Если l₂, то полная сила, действующая на проводник конечной длины l₁-r
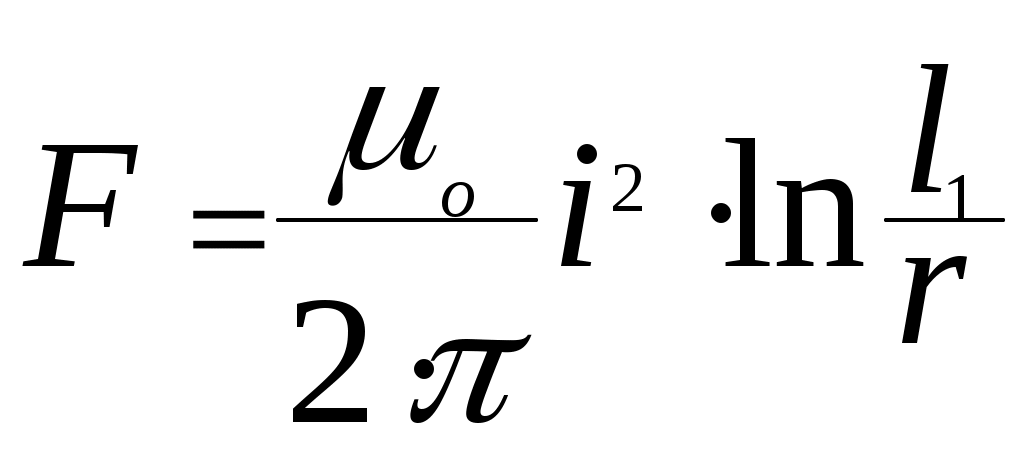, (12)
где r – радиус круглого проводника.

Если l₂ конечная длина, то полная сила, действующая на проводник конечной длины l₁-r

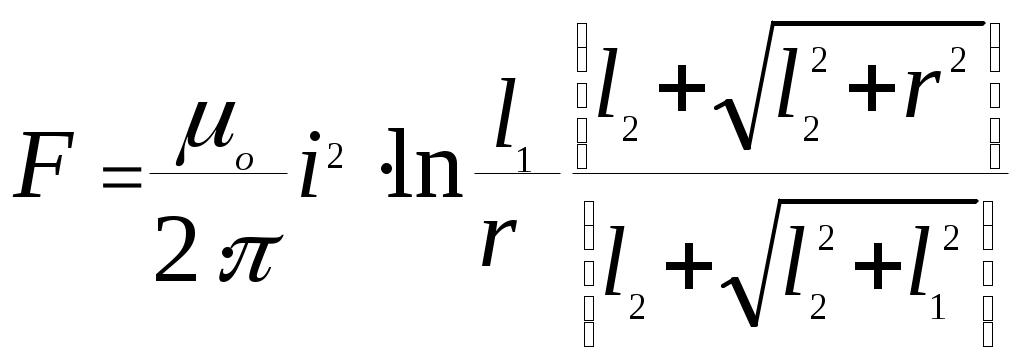(13)
Рассмотренные случаи взаимного расположения проводников параллельно друг другу и под прямым углом имеют широкое распространение в электрических аппаратах.

2. 
   Электродинамические силы в круговом витке
   

В круговом витке с током iвозникают радиальные силы f стремящиеся увеличить его периметр, т.е. разорвать виток.



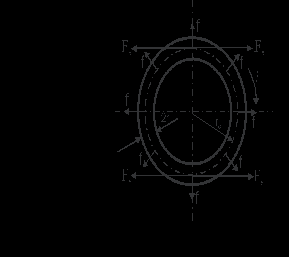
Рис. 4. Электродинамические силы в круговом витке
Электродинамическая сила, действующая на весь виток, рассчитывается по формуле:



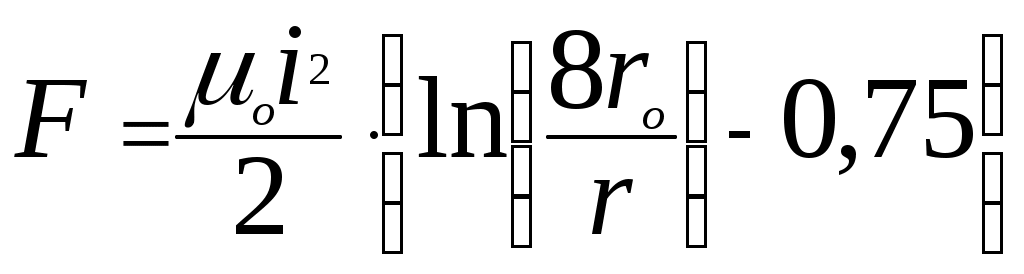(14)
Электродинамическая сила F_x, стремящаяся разорвать виток, определяется как сумма горизонтальных составляющих сил f на четверти длины окружности:
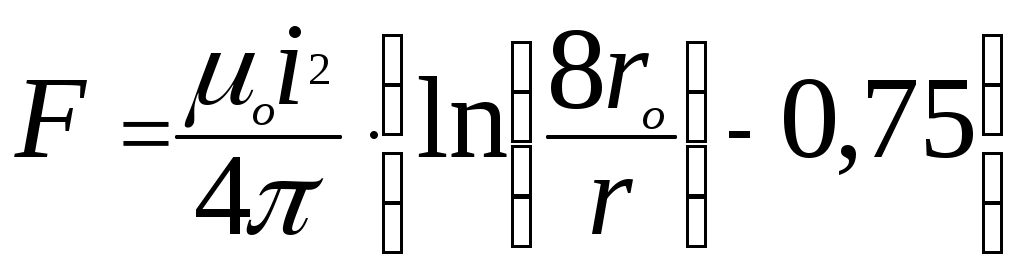(15)

3. 
   Электродинамические силы в месте изменения сечения проводника
   

При изменении поперечного сечения проводника происходит искривление линий тока. Так как сила dF нормальна к линиям тока, то она наклонена в сторону большего сечения. Эту силу можно разложить на две составляющие: поперечную сжимающую dF

---