Файл: 1. 1 Переход к фнчпрототипу и нормирование по частоте.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.11.2023
Просмотров: 17
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
1. Синтез электрического фильтра
1.1 Переход к ФНЧ-прототипу и нормирование по частоте
Определим нормированные граничные частоты ФНЧ-прототипа для полосового фильтра:
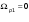 ;
; 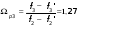
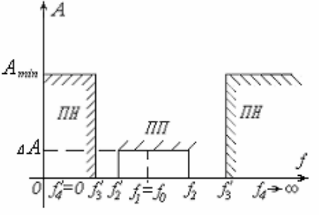
Рис. 1.1 Характеристика технических требований полосового фильтра
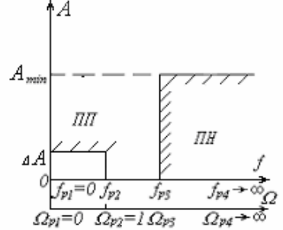
Рис. 1.2 Характеристика технических требований ФНЧ-прототипа
1.2 Аппроксимация частотной характеристики рабочего ослабления фильрта
Для аппроксимации передаточной функции будем применять полиномы Чебышева. При этом квадрат функции фильтрации определяется следующим выражением:
Рассчитаем максимально допустимое значение рабочего ослабления в ПП через формулу связи с коэффициентом отражения:
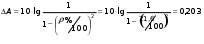
Тогда коэффициент неравномерности рабочего ослабления в полосе пропускания

Определим порядок фильтра n:
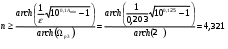
Округлив в большую сторону, примем n = 5. Полином Чебышева определим с использованием рекуррентной формулы:
Найдем полином Чебышева:
Отсюда
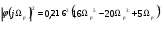 .
.Сформируем рабочую передаточную функцию:
где
Рассчитаем корни
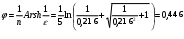
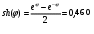 ;
; 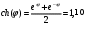
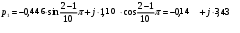
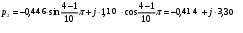
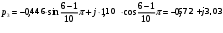
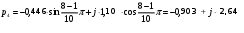
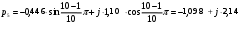
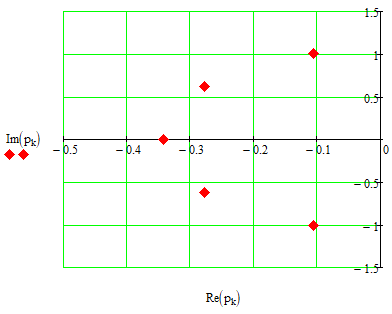
Рис. 1.3 Изображение корней полинома Гурвица на комплексной плоскости
Подставляя полученные корни в передаточную функцию, получим:
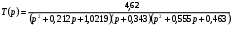
Найдем функцию рабочего ослабления:

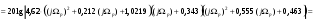
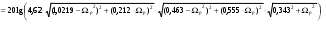
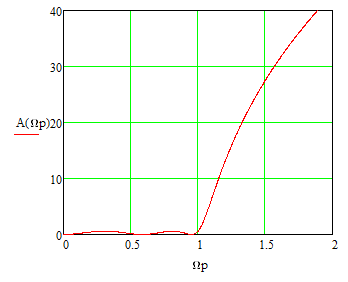
Рис. 1.4 График зависимости рабочего ослабления от нормированной частоты
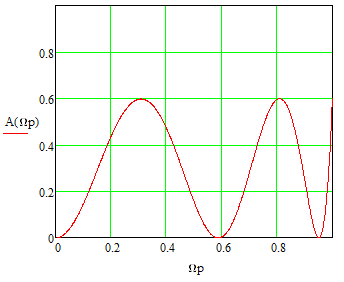
Рис. 1.5 График зависимости рабочего ослабления от нормированной частоты в ПП
Проверим полученное выражение рабочего ослабления:
1. При
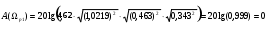 дБ
дБ2. При
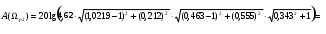
=
3. При
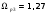 :
: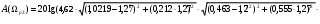
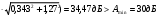
Можно сделать вывод, что рабочее ослабление отвечает техническим требованиям.
2.Реализациясхемыфильтра
2.1РеализациясхемыФНЧ-прототипапометодуПопова
РеализациюсхемыФНЧ-прототипапроведемпометодуПопова.Внашемслучаепорядокфильтраnявляетсянечетным.
Длякаждойпарыкомплексно-сопряженныхкорней
Сформируемполиномы
Найдемкоэффициент
Составимфункцию
:
РазложимполученнуюфункциювцепнуюдробьпоКауэру:
Такимобразом,

Наосновеполученногоразложенияпостроимнормированнуюсхемуправойполовиныфильтра:
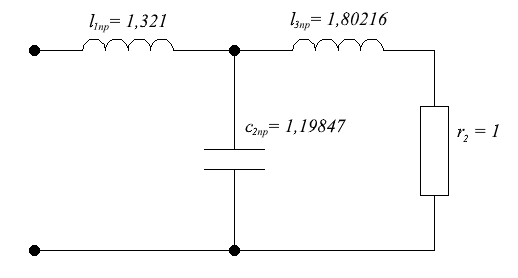
Рис.2.1Праваяполовинасинтезируемогофильтра
Всоответствиисусловиемсимметрииреализуемлевуюполовинуфильтра:
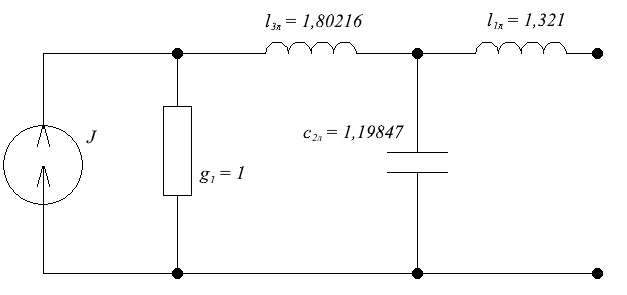
Рис.2.2Леваяполовинасинтезируемогофильтра
Объединимдвеполовиныфильтраизаменимисточниктокаэквивалентнымисточникомнапряжения,получивполнуюнормированнуюсхемуфильтра:
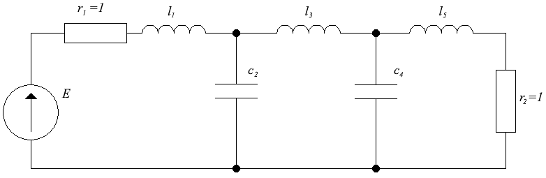
Рис.2.3Схемафильтра,полученнаяобъединениемправойилевойчастей
2.2ПереходотнормированнойсхемыФНЧ-прототипаксхемезаданногофильтра
ПреобразуемпередаточнуюфункциюФНЧ-прототипавфункциюполосовогофильтра.Дляэтоговоспользуемсяследующимсоотношением:
ПриэтомсовершаетсяпереходксхемеПФ,гдекаждаяиндуктивностьпереходитвпоследовательныйконтурсэлементами
акаждаяемкость
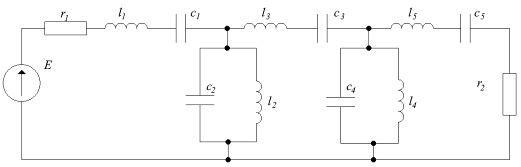
Рис.2.4Нормированнаясхемаполосовогофильтра

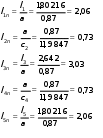
Найдемпреобразующиемножителисопротивленияичастоты:
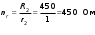
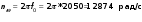
Коэффициентыденормирования:
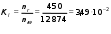 Гн
Гн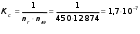 Ф
Ф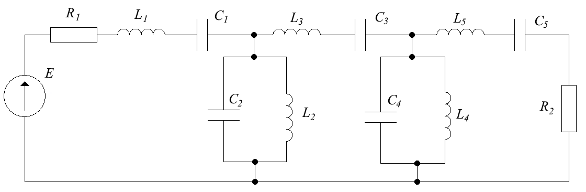
Рис.2.5Денормированнаясхемаполосовогофильтра
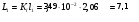 мГн
мГн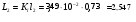 мГн
мГн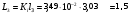 мГн
мГн мГн
мГн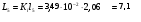 мГн
мГн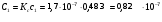 Ф
Ф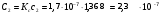 Ф
Ф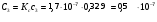 Ф
Ф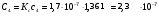 Ф
Ф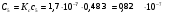 Ф
Ф