Файл: Полное исследование функции Построение графиков.docx

МИНИСТЕРСТВО ОБРАЗОВАНИЯ ОРЕНБУРГСКОЙ ОБЛАСТИ

ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ПРОФЕССИАНАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

«ОРЕНБУРГСКИЙ КОЛЛЕДЖ ЭКОНОМИКИ И ИНФОРМАТИКИ»

(ГАПОУ ОКЭИ)

Глебова Татьяна Александровна

Индивидуальный проект на тему:



«Полное исследование функции Построение графиков»

Направление подготовки – 09.02.07 Информационные системы и программирование (квалификация: специалист по информационным системам)

Группа-1ис3

РУКОВОДИТЕЛЬ _______________ О. Д. Литвиненко

подпись

«___» _______2023 г.

КОНСУЛЬТАТ _______________ О. И. Селищева

подпись

«___» _______2023 г.

г. Оренбург, 2023 г

Оглавление

Глава 1. Теоретическая часть проекта

1.1 Схема полного исследования

1. Областью определения функции называется множество значений аргумента, на котором можно задать эту функцию.

2. Функция чётная , если для любого X из области определения выполняется равенство f(-X) = f(X). Функция нечётная , если для любого X из области определения выполняется равенство f(-X) = -f(X).

3.Нули функции – это значение аргумента, при которых функция обращается в нуль.

3.Знакопостоянство - это промежутки, где функция сохраняет знак.

4. Промежутки монотонности функции – промежутки функции, на которых функция либо возрастает, либо убывает.

---

5 . Функция f(X) называется непрерывной в точке X_O, если предел функции в точке X_O существует и

6. 
   Асимптотой называется прямая, к которой неограниченно (не пересекая) приближается кривая графика функции.
   

6. 
   Экстремумы функции - точки минимума или максимума.
   

6. 
   Промежутки монотонности функции – промежутки функции, на которых функция либо возрастает, либо убывает.
   

9.Если на некотором интервале вторая производная функции сохраняет знак «+» для всех точек интервала, то на этом интервале функция вогнута. Если на некотором интервале вторая производная для всех точек интервала, то на этом говорят, что функция выпукла.

Точка перегиба функции – это точка, в которой меняется характер выпуклости графика функции. 

Глава 2. Исследование функции

1.



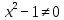
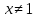
D_y =

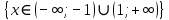
2 . Ox: , точка (0;0)

Oy: x = 0, 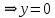, точка (0;0)

3.

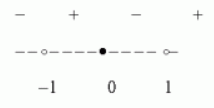
Y<0,

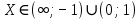
Y>0,

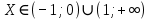
4

---

.

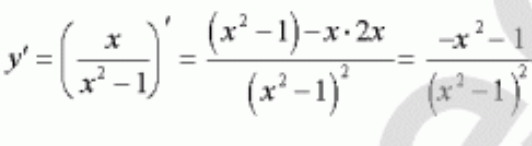
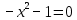
(-∞;-1)	(-1;1)	(1;+∞)
f(x)<0	f(x)<0	f(x)<0
Функция убывает	Функция убывает	Функция убывает

Y

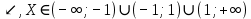
5. Т.к. Y 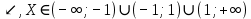, то экстремумов у данной функции нет.

6. Проверим функцию на чётность и нечётность



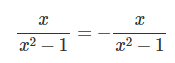
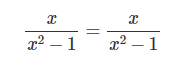
Функция является нечётной, так как график симметричен относительно начала координат.

7 .

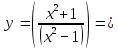
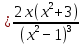
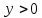вогнутая 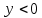выпуклая

На промежутках 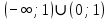функция выпуклая

На промежутках 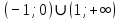функция вогнутая

8. Функция прерывается в точках -1 и 1

Вертикальные асимптоты находятся в точках разрыва, т.е в точках -1 и 1

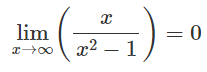
Г 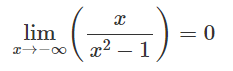оризонтальные асимптоты можно найти с помощью пределов в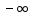

---

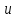
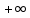
Горизонтальные асимптоты слева и справа находятся в точке 0 и совпадает с осью Ox.



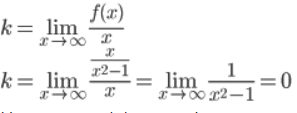
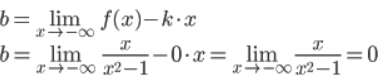
Наклонные асимптоты совпадают с горизонтальной асимптотой

Глава 3. Технологическая карта

3.1 Таблица 1- технологическая карта

Для того, чтобы мои действия были понятны, я описал ход действий в таблице 1. По ней видно какие я брал инструменты, весь ход работы, а также что в итоге получилось.

В таблице номер 2 я резюмировал знания, полученные во время исследования графика функции.

Инструменты	Ход работы	Результат
Миллиметровая бумага, карандаш	На бумаге делаем набросок графика	Набросок
Линейка	При помощи карандашных линий и линейки дорисовываем график	Готовый график

3.2 Шаги исследования

Шаг исследования	Результат
Область определения	Dy =
Точки пересечения с осями	Ox = (0;0) Oy = (0;0)
Промежутки знакопостоянства	Y<0, 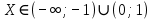Y>0,
Промежутки монотонности	Y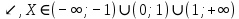
Экстремумы	Точек мин и мах не имеет
Чётность, нечётность	Нечётная, т.к график симметричен относительно начала координат
Выпуклость, вогнутость	На промежутках функция выпуклая, а на промежутках функция вогнутая
Непрерывность, асимптоты	Прерывается в точках -1 и 1 Вертикальная асимптота находится в точках разрыва Горизонтальные асимптоты слева и справа находятся в точке 0 и совпадает с осью Ox. Наклонные асимптоты совпадают с горизонтальной асимптотой

---

Заключение

Важную роль при исследование функций играет график, используемый при построении математической модели рассматриваемой проблемы. Такое исследование проводится с учётом свойств конкретных функций и позволяет уточнить сформулированную математическую задачу, решая которую, рассчитывают получить определённый результат, требующий в дальнейшем интерпретации в исследуемой функции.График помогает увидеть нужную информацию сразу, он может помочь решить какую-либо задачу.Графики могут помочь как в профессиональной деятельности, как в учёбе и в проектах.

Список используемых источников

1. А.Г.Мордкович, П.В. Семенов. Алгебра 10 класс. Базовый и углубленный уровень. 2020 г.

2.https://www.matburo.ru/ex_ma.php?p1=maissl

3. http://www.yotx.ru/

4. https://www.youtube.com/watch?v=jG_pM3EHAoI

5.https://www.evkova.org/issledovanie-funktsii

---