Файл: Расчет схемы амплитуднофазовой частотной характеристики эхс.rtf
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.01.2024
Просмотров: 44
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Министерство образования и науки Российской Федерации
Федеральное государственное автономное образовательное учреждение высшего образования
«Новосибирский национальный исследовательский государственный университет»
(Новосибирский государственный университет)
Структурное подразделение Новосибирского государственного университета
Высший колледж информатики Университета
КАФЕДРА ЕСТЕСТВЕННОНАУЧНЫХ ДИСЦИПЛИН
Расчет схемы амплитудно-фазовой частотной характеристики ЭХС
Введение
Цель: убедится в перспективности способа измерения импеданса ЭХС с предварительной компенсацией сопротивления электролита и емкости двойного электрического слоя. Используемые сокращения для обозначения параметров:
Re - сопротивление электролита;
Rp - сопротивление электродной границы
Cd- емкость двойного электрического слоя и константы стадии диффузии, константы А Варбурга.;- импеданса Варбурга=1000 - Константа Варбурга, Ом/сек^-1/2;
Методы расчета
Zdl = A./sqrt(w*(1-j)
=100; Значение объемного сопротивления электролита.=10^-5; Значение параметра Cd - емкость двойню эл. слоя.=1000; Значениесопротивления перехода R3=Rp.
=j.*w*Cd+1. /(R3+Zdl)
Адмиттанс электродной границы без Ro.
=R2+1. /y3
Импеданс исследуемого ЭХО.R2 - сопротивление электролита=min(imag(Zio)) поиск экстремального значения
e=abs(ImZiomin*2)
=abs(R3-R3e); абсолютная погрешность определения сопротивления Re=R3e.=(dR3/R3) *100; относительная погрешность определения Re=R3e.
Используя уравнение w*Cd*R3=1, зная частоту w в точке минимума и зная R3,можно определить значение Cd.
Cde=1/(75*R3e)=abs(Cd-Cde)=(dCd/Cd) *100=10^4=min(real(Zio)); Rk=100e=abs(Rk);=abs(R2-R2e);=(dR2/R2) *100;=1. /Zio;=10^-10;
R0=10^6;=1. /(j.*w*C0+(1/R0))
входной импеданс измерительной цепи. Учтемшунтирующее влияние измерителя на исследуемый импеданс Zio ЭХО.
. Непосредственно по частотной характеристике можно определить параметры схемы замещения ИО с импедансом Zio=R2+1. /y3. В этом случае сопротивление электролита определяется с погрешностью, порядка 0,02.
.Полученная оценка значения сопротивления электрохимической реакции R3=Rp имеют погрешностью порядка 12,5, а погрешность в оценке значения емкости двойного электрического слоя Cd - составляет 18. Это достаточно грубые оценки. Поэтому нужно усовершенствовать импедансный метод.
Применение компенсации для повышения точности измерений параметров Rp и Cd
Методика компенсации емкости cd
1. Введем отрицательное значение проводимости - j*w*Ck и определим:
Yio2=Yio1-j*w*Ck
импеданс сопротивление электрический
2. Определим остаточный импеданс Zio2 после компенсации
Zio2=1. /Yio2
. Строим график годографа импеданса Zio2:
plot(real(Zio2), imag(Zio2)). Видим, что на графике Re отсутствует
. Первоначальное значение Ск возьмем равным определенному выше при анализе частотной характеристики импеданса ИО: Zio=R2+1. /y3 и определенное из соотношения 1= wCdRp, откуда Сd=1/(w*Rp).
. Затем пошагово изменяем значение Ск, одновременно контролируем на каждом шаге поведение мнимой его части годографа
plot(real(Zio2), imag(Zio2))
Если при принятом значении Ск получаем годограф с положительными значениями мнимого компонента, то это указывает, что произошла перекомпенсация Cd. Необходимо сделать шаг назад, т.е. уменьшить Ск на единицу младшего разряда.
Пошагово уменьшаем значение Ck, чтобы получить годограф с отрицательным значением мнимого компонента.
. Строим график зависимости мнимой компоненты от частоты.См. программустроки 100 -103;
i=1: lf; figure plot (i, imag(Zio2))
7. При сползании впроцессе регулирования Ск экстремума влево от первоначального положения увеличиваем верхнюю частоту fmax в нашем численном эксперименте. Следим за формой годографа, он должен иметь четко выраженный минимум
. Определяем индекс i частоты, соответветствующий минимальному значению мнимой компоненты.
.Для определения параметра Rp воспользуемся теоретическим соотношением, что в точке экстремума справедливо соотношение Rp=2*abs(MIZ2)
В нашей работе значение индекса i равно 156, Ск - нам известно, мы его подбирали (регулировали) сами при компенсации Сd. Частота, соответствующая этому индексу w (156) = 9.7452e+003 Гц.
При этом Rp= 1/(w*dCk) = 1.0261e+003 Ом.
Метод определения импеданса по с предварительной компенсацией сопротивления электролита re=|-rk| и емкости двойного слоя cd
. Используем на первом шаге численного эксперимента компенсацию сопротивления электролита, тогда Zio1=Zio -Rk. Определим Rk.
В натурном эксперименте это легко осуществить компенсацию Re с помощью мостовой измерительной цепи. В нашем "численном эксперименте" мы это произведем вычитанием из общего импеданса значения сопротивления электролита Re. Численно значение
Re=min(real(Zio)), т.е. Re=|-Rk|= min(real(Zio))
Построим годограф импеданса Zio1 с компенсацией сопротивления электролита
Zio1=Zio-Rk;=real(Zio1);1=imag(Zio1);
Попытаемся определить параметры Cd, сопротивления Rp более точно.=R2; сопротивление электролита Rp=R3;
Преобразуем импеданс Zio1 в комплексную проводимость
Yio1=1. /Zio1;
Попытаемcя скомпенсировать емкость двойного слоя. В качестве первогоприближения выбираем
=9.95*10^-6
Yio2=Yio1-j*w*Ck;=1. /Yio2;=min(imag(Zio2))(imag(Zio2) ==MIZ2) ind=156.=1: lw;=w (i (156)) wi= 9.7452e+003.
Определение параметров электродной границы и их погрешностей.
dCk=abs(Cd-Ck), dCk=1.0000e-007
абсолютная погрешность определения Ск.
=100*dCk/10^-5, oCk=1.0000
относительная погрешность определения Ск.
dCk = 5.0000e-008, oCk = 0.5000.
Rp=2*abs(MIZ2)=abs(R3-Rp)
абсолютная погрешность определения Rp.=Drp/10- относительная погрешность определения Rp.
= 1.0082e+003, Drp = 8.1738, Orp = 0.8174.
Определим значение константы Варбурга. Для этой цели воспользуемся значениями мнимой компоненты imag(Zio2(1) и imag(Zio2(2) на первой (1) и второй (2) низких частотах.
Im1=abs(imag(Zio2(1)));=abs(imag(Zio2(2)));=2*pi*f (1);=abs(1/sqrt(w1));=2*pi*(f (2));=abs(1/sqrt(w2));=(Im1+Im2)/abs(a1+a2)= A-1000=dA/10= 1.0093e+003
odA= 0.9334.
.Используя импеданс-частотный метод, т.е. метод определения зависимости импеданса ЭХО от частоты, можно с достаточной высокой точностью определитьсопротивление электролита и его скомпенсировать.
. Подключив дополнительно операцию по компенсации емкости двойного электрического слоя, повысить точность измерения компонентов Cd и Rp, не менее, чем на порядок.
Таким образом, методом математического моделирования на данном примерепоказано, что предлагаемое к реализации устройство с предварительной компенсацией параметров: сопротивления электролита Re и емкости двойного электрического слоя Cd потенциально может обеспечить относительные погрешности (o)измерения:оRe=0,01, oCd=0.50;= 1.0082e+003, оRp=0.8174.
Относительная погрешность определения константы Варбурга odA= 0.9334
Следовательно, используя сочетание методов:
. Определения частотной зависимости импеданса исследуемого объекта и предварительной оценки значений искомых параметров Re, Rp и Cd;
. Компенсации сопротивления электролита Re и емкости двойного электрического слоя Cd;
. можно практически более чем на порядок повысить точность определения искомых компонентов Rp, Cd и константы Варбурга, а полученные результаты подтверждают перспективность предложенного принципа предварительной компенсации сопротивления электролита Re и емкости двойного электрического слоя Cd для построения "цифрового измерителя параметров двух- и трехполюсных электрических объектов".
Графики
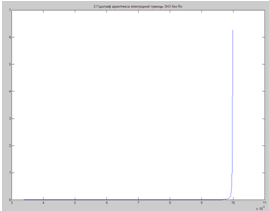
Годограф импеданса Варбурга
X=real(Zdl)
Y=imag(Zdl)
Годограф адмиттанса электродной границы ЭХО без Ro
X=real(y3)=imag(y3)
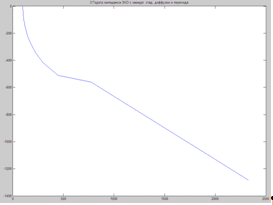
Годограф импеданса ЭХО с замедленными стадиями диффузии и перехода
X=real(Zio)
Y=imag(Zio)

Годограф мнимого компонента импеданса исследуемого ЭХО
X=w=imag(Zio)
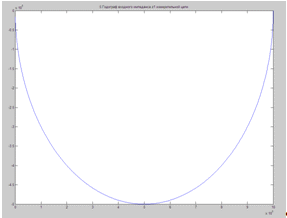
Годограф входного импеданса z1 измерительной цепи
X=real(z1)=imag(z1)
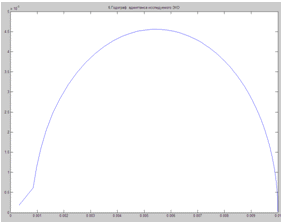
Годограф адмиттанса исследуемого ЭХО
X=real(y2),
Y=imag(y2)
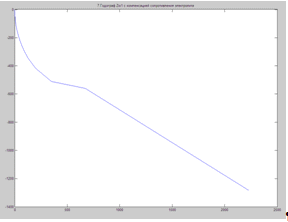
Годограф Zio1 с компенсацией сопротивления электролита
X=ReZio1
Y=ImZio1
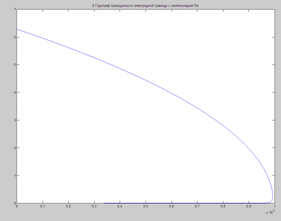
Годограф проводимости электродной границы с компенсацией Re
X=real(Yio1)=imag(Yio1)
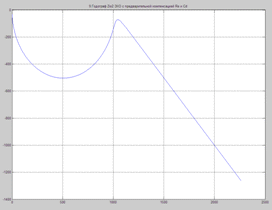
Годограф Zio2 ЭХО с предварительной компенсацией Re и Cd
X=real(Zio2)=imag(Zio2)
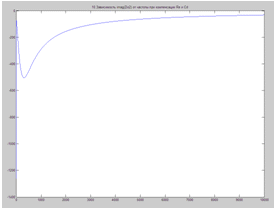
Зависимость imag(Zio2) от частоты при компенсации Re и Cd
X=i=imag(Zio2)