ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.01.2024
Просмотров: 50
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Лабораторная работа
Изучение ассиметричного алгоритма шифрования RSA
Лабораторная работа состоит из двух программ:
-
первая программа RSA.exe представляет собой реализацию в обучающем режиме алгоритма RSA. -
вторая программа DemoRSA.exe позволяет в демонстрационном режиме наглядно увидеть этапы работы алгоритма RSA на конкретном примере генерации открытого и закрытого ключа, шифрования/дешифрования информации.
1ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
1.1Основы работы с программой
При запуске программы (файл RSA.exe) появляется главная форма (см. рис 1), в которой и будет происходить вся дальнейшая работа. Форма имеет главное меню программы, куда входят такие пункты как «Вызов деморежима», «Вызов справки», «О программе» и «Выход».
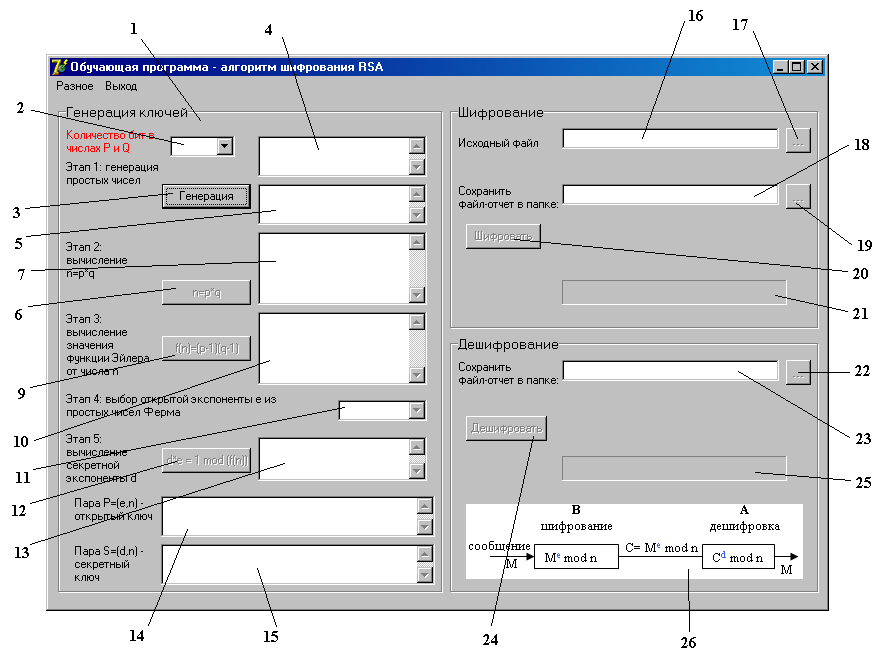
Рис.1 - Главное окно программы Rsa.exe
На рисунке приняты следующие обозначения:
1 – главное меню программы;
2 – окно выбора количества бит в числах p и q;
3 – кнопка генерации случайных простых чисел p и q в соответствии с размером, выбранным в окне 2;
4 – поле ввода/отображения сгенерированного простого числа q;
5 – поле ввода/отображения сгенерированного простого числа q;
6 – кнопка вычисления произведения n=p*q;
7 – поле отображения произведения;
9 – кнопка вычисления функции Эйлера от числа n;
10 – поле отображения значения функции Эйлера от числа n;
11 – окно выбора открытой экспоненты e из простых чисел Ферма;
12 – кнопка вычисления секретной экспоненты d;
13 – поле отображения секретной экспоненты d;
14 – поле отображения открытого ключа;
15 – поле отображения секретного ключа;
16 – поле отображения пути к исходному файлу;
17 – кнопка, при нажатии на которую открывается диалоговое окно выбора исходного файла, который требуется зашифровать;
18 – поле отображения пути к папке, в которую сохранится файл отчета о процессе шифрования;
19 – кнопка, при нажатии на которую открывается диалоговое окно выбора папки для сохранения отчета;
20 – кнопка, при нажатии на которую начинается процесс шифрования входного файла или строки;
21 – прогресс-бар, показывающий, какая часть файла обработана;
22 – кнопка, при нажатии на которую открывается диалоговое окно выбора папки для сохранения отчета;
23 – поле отображения пути к папке, в которую сохранится файл отчета о процессе дешифрования;
24 – кнопка, при нажатии на которую начинается процесс дешифрования;
25 – прогресс-бар, показывающий, какая часть файла обработана;
26 – картинка, изображающая процесс шифрования и дешифрования информации с помощью ассиметричного алгоритма RSA.
При наведении курсора мыши на поля вывода информации и чисел появляются всплывающие подсказки. Например, поле на этапе «Вычисление значения функции Эйлера от числа n» имеет подсказку, представленную на рис.2.

Рис.2 – Всплывающая подсказка
Существует возможность вызвать демонстрационный модуль в главной форме из меню. Окно деморежима представлено на рис.3.
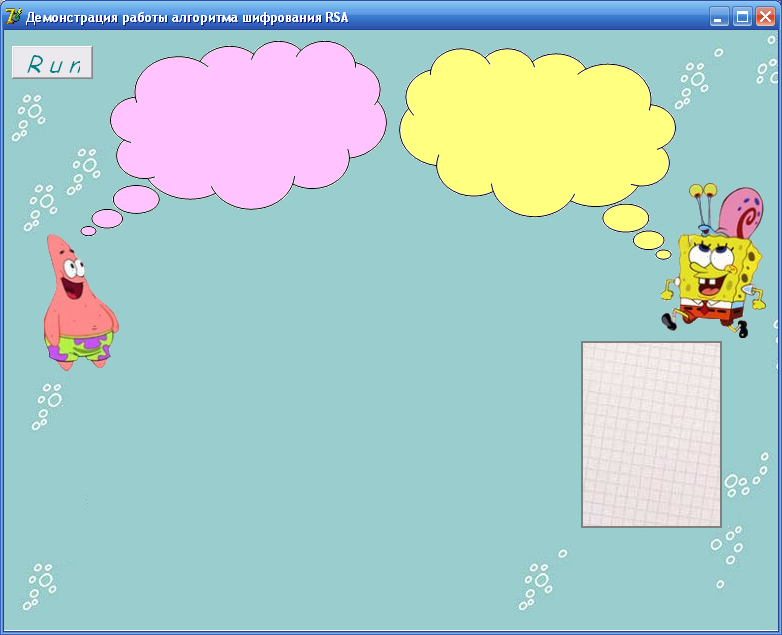
Рис.3 – Окно демонстрационного режима
При нажатии на единственную на форме кнопку Run, начинается демонстрация работы алгоритма шифрования. Можно просто наблюдать, как происходит генерация ключей и шифруется, а затем и дешифруется некоторый текст.
Для большей наглядности в деморежиме генерируется ключ небольшой разрядности, и шифруемый текст состоит всего из четырех символов.
1.2Краткая теория
Основой для лабораторной работы является алгоритм шифрования с открытым ключом RSA.
RSA (буквенная аббревиатура от фамилий Rivest, Shamir и Adleman) - криптографический алгоритм с открытым ключом. RSA стал первым алгоритмом такого типа, пригодным и для шифрования, и для цифровой подписи. Алгоритм используется в большом числе криптографических приложений.
В криптографической системе с открытым ключом каждый участник располагает как открытым ключом (public key), так и секретным ключом (secret key). Каждый ключ - это часть информации. В криптографической системе RSA каждый ключ состоит из пары целых чисел. Каждый участник создаёт свой открытый и секретный ключ самостоятельно. Секретный ключ каждый из них держит в секрете, а открытые ключи можно сообщать кому угодно или даже публиковать их. Открытый и секретный ключи каждого участника обмена сообщениями образуют «согласованную пару» в том смысле, что они являются взаимно обратными.
Алгоритм RSA состоит из следующих пунктов:
-
Выбрать простые числа p и q заданного размера (например, 512 битов каждое).
В криптографии под случайным простым числом понимается простое число, содержащее в двоичной записи заданное количество битов k, на алгоритм генерации которого накладываются определенные ограничения.
-
Вычислить n = p * q -
Вычисляется значение функции Эйлера от числа n:
m = (p - 1) * (q - 1)
-
Выбрать число d взаимно простое с m
Два целых числа называются взаимно простыми, если они не имеют никаких общих делителей, кроме ±1. Примеры: 14 и 25 взаимно просты, а 15 и 25 не взаимно просты (у них имеется общий делитель 5).
-
Выбрать число e так, чтобы e * d = 1 (mod m)
Числа e и d являются ключами. Шифруемые данные необходимо разбить на блоки - числа от 0 до n - 1.
Шифрование и дешифровка данных производятся следующим образом:
Шифрование: P(M) = Me mod n
Дешифровка: S(C) = Cd mod n
Следует также отметить, что ключи e и d равноправны, т.е. сообщение можно шифровать как ключом e, так и ключом d, при этом расшифровка должна быть произведена с помощью другого ключа.
Схема шифрования и дешифрования RSA представлена на рис.4. Предположим, сторона B хочет послать стороне А сообщение М. Сообщением являются целые числа от 0 до n-1.

Рис.4 – Схема шифрования/дешифрования RSA
Размер ключа в алгоритме RSA связан с размером модуля n. Два числа p и q, произведением которых является модуль, должны иметь приблизительно одинаковую длину, поскольку в этом случае найти сомножители (факторы) сложнее, чем в случае, когда длина чисел значительно различается. Например, если предполагается использовать 768-битный модуль, то каждое число должно иметь длину приблизительно 384 бита. Обратите внимание, что если два числа чрезвычайно близки друг к другу или их разность близка к некоторому предопределенному значению, то возникает потенциальная угроза безопасности, однако такая вероятность – близость двух случайно выбранных чисел – незначительна.
Оптимальный размер модуля определяется требованиями безопасности: модуль большего размера обеспечивает большую безопасность, но и замедляет работу алгоритма RSA. Длина модуля выбирается в первую очередь на основе значимости защищаемых данных и необходимой стойкости защищенных данных и во вторую очередь – на основе оценки возможных угроз.
На 2009 год система шифрования на основе RSA считается надёжной, начиная с размера n = p * q в 1024 бита. В лабораторной работе предлагается выбрать размер чисел p и q, и сгенерировать ключ размерами 64 (при выборе размерности простых чисел из выпадающего списка – 32 бита), 128, 256, 512, 1024 бита.
Более подробную информацию о данном алгоритме шифрования и конкретные примеры можно получить из справки, а также из источников, указанных в литературе.
2Практическая часть
-
Ознакомиться с теоретической частью данной лабораторной работы.
-
Запустить файл RSA.exe и изучить интерфейс программы.
-
Запустить из меню программы деморежим и просмотреть его до конца.
-
Постараться реализовать разобранный пример:
4.1. Выбрать из выпадающего списка размерность чисел p и q. Для начала это будет 32 бита. Следовательно, ключ будет 64-битный.
4.2. С помощью генератора случайных простых чисел сгенерировать p и q (кнопка «Генерация»).
4.3. Нажатием на соответствующие кнопки вычислить n и f(n).
4.4. Из выпадающего списка выбрать открытую экспоненту. Пусть это будет 17.
4.5. Нажать на кнопку, вычисляющую секретную экспоненту. В полях для вывода открытого и закрытого ключа будут примерно такие числа, как на рис.5.
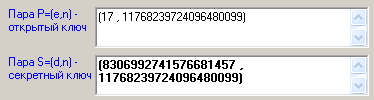
Рис.5 – Ключи сгенерированы
Вставьте в отчет по лабораторной работе эти ключи.
4.6. Выбрать текстовый файл размером 1 байт (то есть в файле должен быть один символ). Выбрать папку для сохранения зашифрованного файла.
4.7. Нажмите на кнопку «Шифровать». Посмотрите размер зашифрованного файла. Его название будет таким: название исходного файла + ‘_crypt’. Объясните, почему 1 байт информации шифруется столькими байтами при ключе размером 64 бита. Выводы и сам зашифрованный текст вставьте в отчет.
4.8. Зашифруйте файл размером от 8 до 16 байт, то есть 8-16 символов. Посмотрите размер полученного файла. Объясните, выводы вставьте в отчет.
4.9. Нажмите на кнопку «Дешифровать». Теперь вы видите, как восстанавливается исходный файл. Его название будет таким: название исходного файла + ‘_decrypt’.
5. Проделать все действия, описанные в пункте 4, для ключа размером 1024 бита. Для этого выбрать размерность чисел p и q 512 бит. В отчет вставить выводы по пунктам, а также ключи и содержимое исходного, зашифрованного и дешифрованного файлов.
-
Проверка алгоритма на помехоустойчивость:
Сгенерировать ключи произвольной длины. Зашифровать и дешифровать некоторый небольшой файл (меньше 350 байт – для шифрования файла большего размера потребуется слишком много времени, RSA – медленный алгоритм). Затем изменить один символ в шифрованном файле и попытаться дешифровать. Вставить в отчет результат и сделать выводы.
-
Проверка алгоритма на криптостойкость:
Сгенерировать ключи произвольной длины. Зашифровать и дешифровать некоторый небольшой файл. Изменить один символ в закрытом (секретном) ключе. В поле, изображенном на рис.6.

Рис.6 – В этом поле нужно изменять секретный ключ
Дешифровать файл таким ключом. Результат и выводы оформить в отчет.
-
Сгенерировать ключи произвольной длины. Для шифрования выбрать любой нетекстовый файл, например, с расширением .bmp. Зашифровать и дешифровать его. Удалить из названия дешифрованного файла «_decrypt», убедиться, что он полностью идентичен исходному.
8. Проверка скорости работы алгоритма:
8.1. Зашифровать небольшой файл (1 Кбайт - 100 Кбайт), и посмотреть время шифрования.
8.2. Дешифровать закодированный файл и посмотреть время дешифрования. Сравнить время шифрования и дешифрования. Сделать выводы. Проверить на работоспособность и корректность преобразования дешифрованный файл.
8.3. Зашифровать большой файл (100 Кбайт - 350 Кбайт), и посмотреть время шифрования.
8.4. Дешифровать закодированный файл и посмотреть время дешифрования. Сравнить время шифрования и дешифрования. Сделать вывод, объяснить, почему файл дешифруется дольше, чем шифруется. Проверить на работоспособность и корректность преобразования дешифрованный файл.
9. Сделать общие выводы по работе. В отчете должны быть вставлены файлы-отчеты.
3СОДЕРЖАНИЕ ОТЧЕТА
Отчет о лабораторной работе должен содержать:
-
Титульный лист -
Цель работы -
Краткую теорию, описывающую алгоритм RSA. -
Подробное описание проделанных экспериментов по пунктам 4 - 8, со всеми выводами и объяcнениями.
4ЛИТЕРАТУРА
-
Прикладная криптография. Протоколы, алгоритмы, исходные тексты на языке Си. Б. Шнайер- М.: Издательство Триумф, 2002-816с. -
http://www.e-nigma.ru/stat/rsa/ -
http://ru.wikipedia.org/wiki/RSA -
http://www.cybersecurity.ru/manuals/crypto/algorithm/1868.html