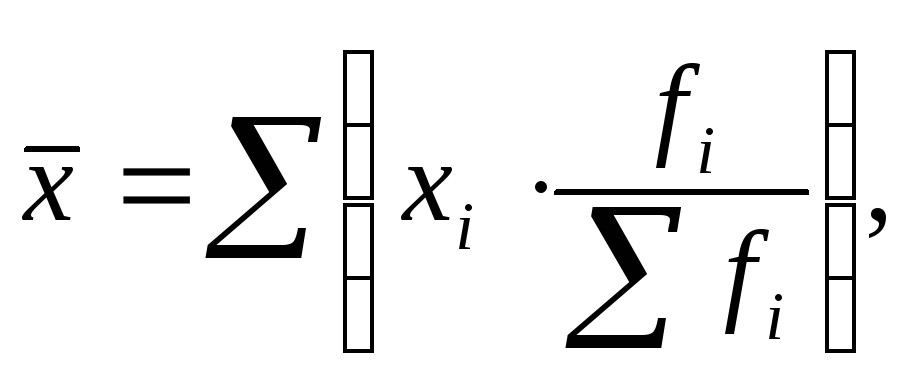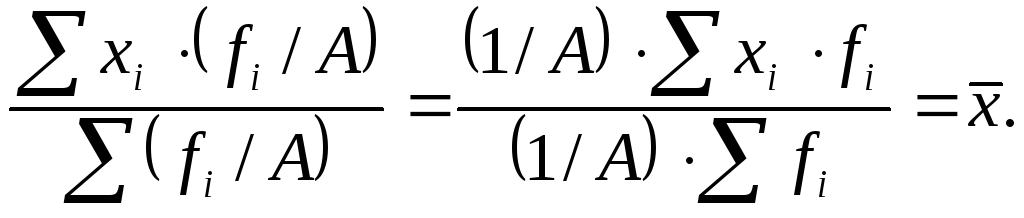Файл: Тема 6.doc

Сущность средней можно раскрыть через понятие ее определяющего свойства: средняя, являясь обобщающей характеристикой всей статистической совокупности, должна ориентироваться на определенную величину, связанную со всеми единицами этой совокупности. Эту величину можно представить в виде функции:

(6.1)

Так как данная величина в большинстве случаев отражает реальную экономическую категорию, ее называют определяющим показателем.

Если в приведенной выше функции все величины заменить их средней величиной, то значение этой функции должно остаться прежним:

(6.2)

Исходя из данного равенства и определяется средняя. Определить среднюю во многих случаях можно через исходное соотношение средней (ИСС) или ее логическую формулу:

Так, например, для расчета средней заработной платы работников предприятия необходимо общий фонд заработной платы разделить на число работников:

Числитель исходного соотношения средней представляет собой ее определяющий показатель

Для каждого показателя, используемого в социально-экономическом анализе, можно составить только одно истинное исходное соотношение для расчета средней.

От того, в каком виде представлены исходные данные для расчета средней, зависит, каким именно образом будет реализовано ее исходное соотношение. В каждом конкретном случае для реализации исходного соотношения потребуется одна из следующих форм средней величины:

• средняя арифметическая;

• средняя гармоническая;

• средняя геометрическая;

• средняя квадратическая, кубическая и т.д.

Перечисленные средние (кроме средней геометрической) объединяются в общей формуле средней степенной (при различной величинеk):

---

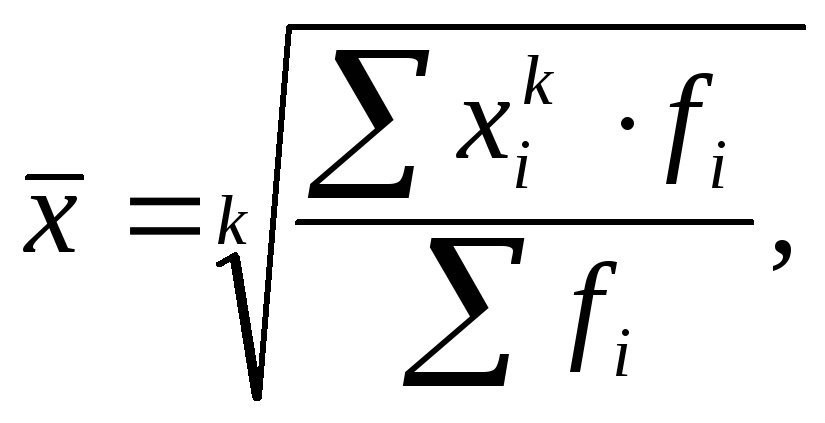
где - средняя величина исследуемого явления;

- i-й вариант осредняемого признака;

- весi-го варианта.

Помимо степенных средних в статистической практике также используются средние структурные, среди которых наиболее распространены мода и медиана.

---

6.5 Средняя арифметическая и ее свойства

Наиболее распространенным видом средних величин является средняя арифметическая, которая, как и все средние, в зависимости от характера имеющихся данных может быть простой или взвешенной.

Средняя арифметическая простая (невзвешенная). Эта форма средней используется в тех случаях, когда расчет осуществляется по не сгруппированным данным.

Используя приведенный в разделе 6.4 условные обозначения, запишем формулу средней:

(6.3)

В этом случае мы использовали формулу средней арифметической простой (невзвешенной).

Средняя арифметическая взвешенная. При расчете средних величин отдельные значения осредняемого признака могут повторяться, встречаться по нескольку раз. В подобных ситуациях расчет средней производится по сгруппированным данным или вариационным рядам, которые могут быть дискретными или интервальными.

Формула средней арифметической взвешенной имеет вид:

(6.4)

В отдельных случаях веса могут быть представлены не абсолютными величинами, а относительными (в процентах или долях единицы). Тогда с учетом несложного преобразования формулы (6.4) получим:

(6.5)

На практике наиболее часто встречающаяся при расчете средних ошибка заключается в игнорировании весов в тех случаях, когда эти веса действительно необходимы. Использовать среднюю арифметическую невзвешенную можно только тогда, когда точно установлено отсутствие весов или их равенство.

При расчете средней по интервальному вариационному рядудля выполнения необходимых вычислений от интервалов переходят к их серединам.

Свойства средней арифметической.Средняя арифметическая обладает некоторымиматематическими свойствами, более полно раскрывающими ее сущность и в ряде случаев используемыми при ее расчетах. Рассмотрим эти свойства.

---

1. Произведение средней на сумму частот равно сумме произведений отдельных вариантов на соответствующие им частоты:

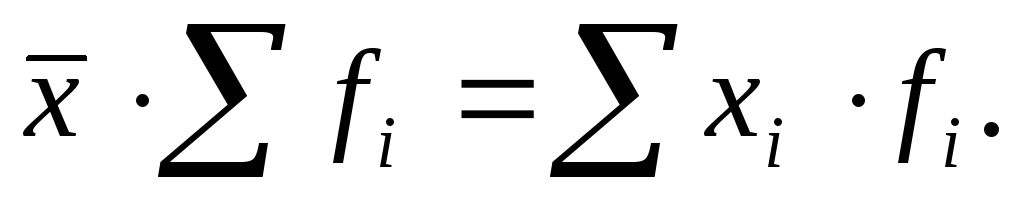
   (6.6)

2. Сумма отклонений индивидуальных значений признака от средней арифметической равна нулю:

(6.7)

Математическое доказательство данного свойства сводится к следующему:

3. Сумма квадратов отклонений индивидуальных значений признака от средней арифметической меньше, чем сумма квадратов их отклонений от любой другой произвольной величины C:

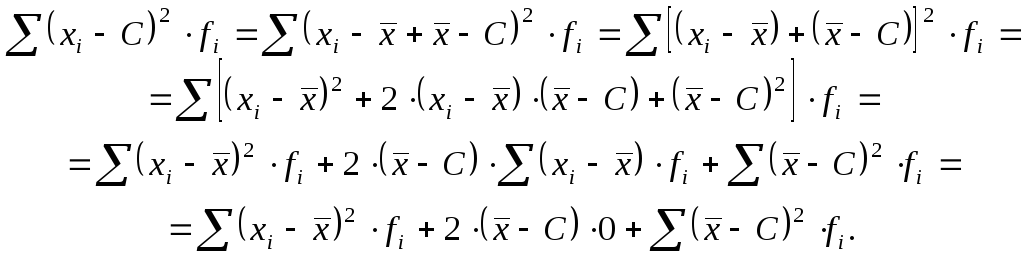
Следовательно, сумма квадратов отклонений индивидуальных значений признака от произвольной величины Cбольше суммы квадратов их отклонений от своей средней на величину:

или

(6.8)

На использовании этого свойства базируется расчет центральных моментов, представляющих собой характеристики вариационного ряда при ¹.

где kопределяет порядок момента (центральный момент второго порядка представляет собой дисперсию).

4. Если все осредняемые варианты уменьшить или увеличить на постоянное число A, то средняя арифметическая соответственно уменьшиться или увеличиться на ту же величину:

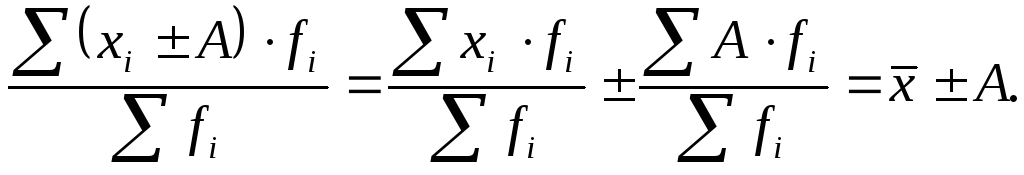
   (6.9)

5. Если все варианты значений признака уменьшить или увеличить в Aраз, то средняя также соответственно увеличится или уменьшится вAраз:

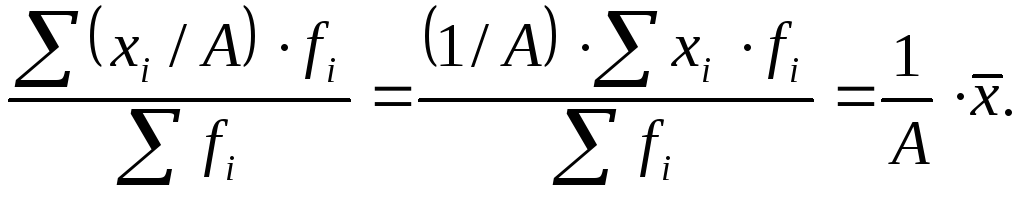
   (6.10)

6. Если все веса уменьшить или увеличить в Aраз, то средняя арифметическая от этого не измениться:

---

(6.11)

Исходя из данного свойства можно заключить, что в случае равенства всех весов между собой расчеты по средней арифметической взвешенной и средней арифметической простой приведут к одному и тому же результату.

---