ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.10.2024
Просмотров: 37
Скачиваний: 0
В табл.1.3 β = I2 I2ном – коэффициент нагрузки трансформатора.
Внешняя характеристика трансформатора U2ф = f (β ), снятая при
U1 = const и cosϕ 2 = 1,0 , представлена на рис. 1.7 сплошной линией.
7. Расчет и построение внешних характеристик
Внешние характеристики можно получить расчетным путем. При любой нагрузке вторичное напряжение определяется так:
U2ф =U2ф.ном (1,0 − 0,01ΔU%),
где U2ф.ном – номинальное фазное напряжение вторичной обмотки трансформатора;
ΔU% – изменение вторичного напряжения при нагрузке, равное
ΔU% = 100(U2ф.ном −U2ф)/U2ф.ном .
При номинальной нагрузке величина ΔU% для силовых трансформаторов составляет 2...5%. С достаточной точностью изменение напряжения можно определить по выражению ΔU% = β(Uа75% cosϕ2 +U p% sinϕ2) .
Задаем значения коэффициента нагрузки: β = 0; 0,5; 0,75; 1,0; 1,25. При заданных значениях cosϕ 2 и sinϕ 2 (разд. 2) рассчитываем ΔU% и U2ф , (табл.).
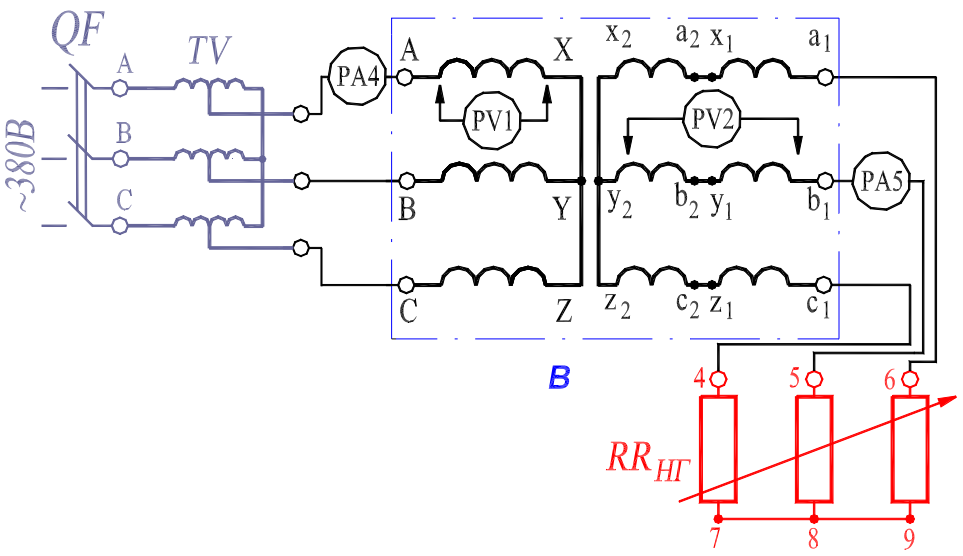
|
b |
Активная |
Активно-индукциооная |
Активно-ёмкостная |
||||
|
Δ U |
U2ф |
Δ U |
U2ф |
Δ U |
U2ф |
||
|
- |
% |
В |
% |
В |
% |
В |
|
|
- |
- |
150,00 |
- |
150,00 |
- |
150,00 |
|
|
0,50 |
3,44 |
139,84 |
3,01 |
139,89 |
2,49 |
151,01 |
|
|
0,75 |
5,15 |
142,28 |
4,52 |
143,6 |
3,73 |
155,52 |
|
|
1,00 |
6,87 |
140,10 |
6,02 |
112,77 |
4,98 |
157,03 |
|
|
1,25 |
8,59 |
137,19 |
7,53 |
138,77 |
6,22 |
159,34 |
|
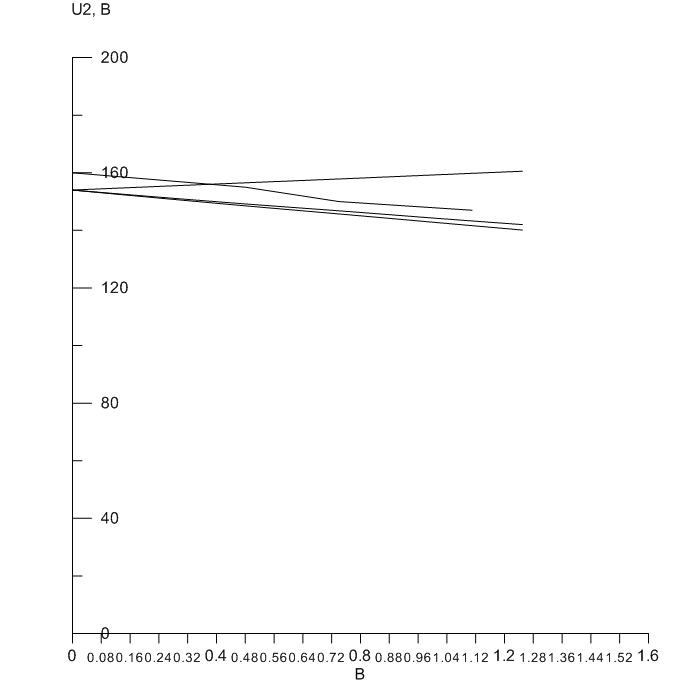
График зависимости U2ф = f (β )
Расчетные внешние характеристики U2ф = f (β ) в одних координатных осях с
опытной внешней характеристикой представлены на рис. 1.7 пунктирной (активная
нагрузка), штрих-пунктирной (активно-индуктивная нагрузка) и штрих-штрих-
пунктирной (активно-емкостная нагрузка) линиями.
8. Расчет и построение зависимости кпд от коэффициента нагрузки
ГОСТ 3484.1–88 рекомендует определять КПД косвенным методом, используя
значения потерь мощности в трансформаторе, получаемые из опытов ХХ и КЗ. Рас-
четное выражение для определения КПД
η = 1,0 – (Рх.ном + β2Рк.ном.75 ).(βSном cosϕ2 + Рх.ном + β2Рк.ном.75 ) ,
где Рх.ном – магнитные потери мощности в магнитопроводе, равные мощности ХХ
при U1x =U1ф.ном ; Рк.ном75 – электрические потери в обмотках, равные мощности
потерь КЗ при I1к = I1ном и температуре 75С , т.е. к75
Рк.ном75 = 3I1номR ;
Sном – номинальная мощность трансформатора.
Используя данные опытов ХХ и КЗ и ряд значений коэффициента нагрузки β ,
рассчитываем КПД при заданном значении коэффициента мощности (табл.).
|
|
β |
- |
0,05 |
0,10 |
0,25 |
0,50 |
0,75 |
1,00 |
1,25 |
|
η |
cosβ=1 |
0 |
0,72 |
0,84 |
0,912 |
0,923 |
0,926 |
0,9201 |
0,906 |
|
|
cosβ=0,8 |
0 |
0,666 |
0,795 |
0,891 |
0,904 |
0,909 |
0,898 |
0,884 |
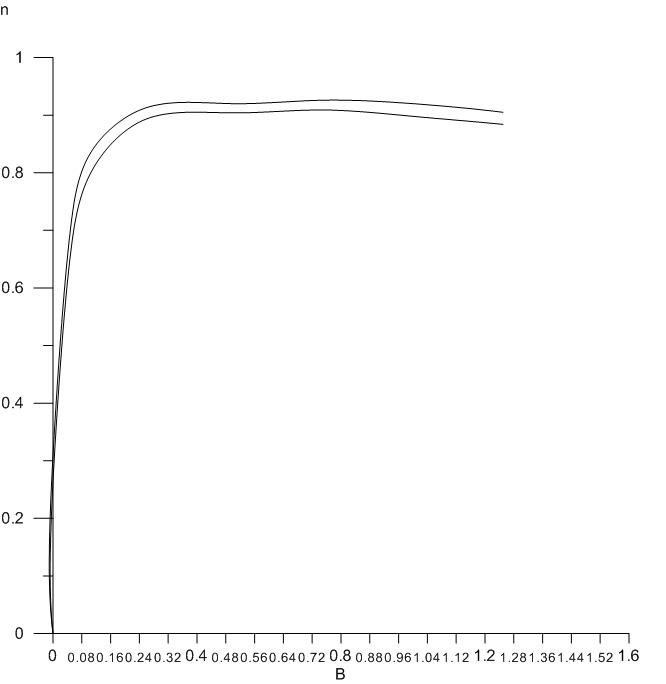
График зависимости η = f (β )
Зависимости η = f (β ) представлены на рис. 1.8 сплошной (cosϕ= 1,0 ) и пунктирной (cosϕ= 0,8 ) линиями.
Кривая η = f (β ) имеет максимум при таком значении β , когда электрические
потери в обмотках равны магнитным потерям в стали. Наиболее вероятная нагрузка, при которой η =η max имеет место, при значении β = 0,5...0,7.
Значение коэффициента нагрузки β , которое соответствует максимальному
значению КПД ηmax , определим по формуле
β опт = Рх.ном /Рк.ном75 .
Максимальное значение КПД
ηmax = 1,0 −(Рх.ном)/(0,5βоптSном cosϕ + Рх.ном).
|
Рх.ном |
Рк.ном75 |
β |
ηmax |
|
|
cosϕ= 1,0 |
cosϕ= 0,8 |
|||
|
50 |
177,2 |
0,529 |
0,929 |
0,9134 |
9. Т-образная схема замещения трансформатора
Трансформатор, у которого обмотки имеют только магнитную связь, может быть
заменен эквивалентной схемой, называемой Т-образной схемой замещения.
В ней сопротивления R1 и X1 определяют первичную обмотку, а R2′ и X2′ – вто-
ричную. Индуктивные сопротивления X1 и X2′ обусловлены магнитными потоками
рассеяния обмоток. Схемы замещения обмоток объединены в точках 1 и 2 намагни
чивающим
контуром с сопротивлениями Rm
и
Xm
.
Индуктивное сопротивление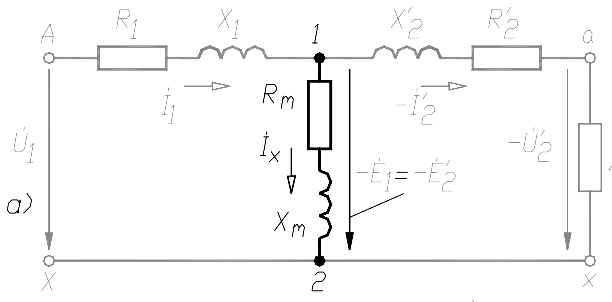
Xm обусловлено основным магнитным потоком, а сопротивление Rm является фик
тивным и его величина определяется потерями мощности в стали магнитопровода.
Сопротивления вторичной обмотки R2′ = k2R, X2′ = k2X и нагрузки Z′нг = k2Zнг приведены к числу витков первичной обмотки. Также приведены значения ЭДС и тока вторичной обмотки: E2′ = kE2 = E1 , I2′ = I2 k , где k =W1 W2 – коэффициент трансформации. Это обеспечивает эквивалентную замену магнитносвязанных цепей электрически связанными цепями. K=1,2
Параметры схемы замещения определяются из опытов ХХ и КЗ трансформатора.
R2′= 0,66 Ом R1= 0,66 Ом
X2′= 0,086 Ом X1=0,086 Ом
E2′= 220 В E1=220 В
I2′= 6,56 A I1= 6,56 А
Rm=45,72 Oм Xm=205,45 Ом