Добавлен: 25.10.2018
Просмотров: 1131
Скачиваний: 16
Применение итоговых функций.1
-
Используя данные из Таблицы 4, продолжите работу.
-
Сделайте текущей следующую свободную ячейку в столбце A.
-
Щелкните на кнопке Автосумма на стандартной панели инструментов.
-
Убедитесь, что программа автоматически подставила в формулу функцию и правильно выбрала диапазон ячеек для суммирования. Нажмите клавишу ENTER.
-
Сделайте текущей следующую свободную ячейку в столбце A.
-
Щелкните на кнопке Вставка функции на стандартной панели инструментов.
-
В списке Категория выберите пункт Статистические.
-
В списке Функция выберите функцию СРЗНАЧ и щелкните на кнопке Ok.
-
Переместите методом перетаскивания палитру формул, если она заслоняет нужные ячейки. Обратите внимание, что автоматически выбранный диапазон включает все ячейки с числовым содержанием, включая и ту, которая содержит сумму. Выделите правильный диапазон методом протягивания и нажмите клавишу ENTER.
-
Используя порядок действий, описанный в п. п. 4-8, вычислите минимальное число в заданном наборе (функция МИН), максимальное число (МАКС), количество элементов в наборе (СЧЕТ).
Таблица 5 Пример применения итоговых функций.
|
|
A |
B |
C |
D |
E |
F |
|
1 |
Результаты измерений |
Удвоенное значение |
Квадрат значения |
Квадрат следующего числа |
Масштабный множитель |
Масштабирование |
|
2 |
-3,00 |
-6,00 |
9,00 |
4,00 |
5,00 |
-15,00 |
|
3 |
10,00 |
20,00 |
100,00 |
121,00 |
|
50,00 |
|
4 |
2,00 |
4,00 |
4,00 |
9,00 |
|
10,00 |
|
5 |
34,00 |
68,00 |
1156,00 |
1225,00 |
|
170,00 |
|
6 |
20,00 |
40,00 |
400,00 |
441,00 |
|
100,00 |
|
7 |
7,00 |
14,00 |
49,00 |
64,00 |
|
35,00 |
|
8 |
-2,00 |
-4,00 |
4,00 |
1,00 |
|
-10,00 |
|
9 |
-30,00 |
-60,00 |
900,00 |
841,00 |
|
-150,00 |
|
10 |
4,00 |
8,00 |
16,00 |
25,00 |
|
20,00 |
|
11 |
-15,00 |
-30,00 |
225,00 |
196,00 |
|
-75,00 |
|
12 |
27,00 |
Сумма |
||||
|
13 |
2,70 |
Среднее значение |
||||
|
14 |
-30,00 |
Минимальное число |
||||
|
15 |
34,00 |
Максимальное число |
||||
|
16 |
10 |
Количество элементов в наборе |
||||
Построение экспериментального графика
-
Выберите щелчком на ярлычке неиспользуемый рабочий лист или создайте новый (Вставка ► Лист). Дважды щелкните на ярлычке листа и переименименуйте его как Обработка эксперимента.
-
В столбец A, начиная с ячейки A1, введите произвольный набор значений независимой переменной.
-
В столбец B, начиная с ячейки B1, введите произвольный набор значений функции.
-
Методом протягивания выделите все заполненные ячейки столбцов A и B.
-
В меню Вставка ► Диаграмма выберите Точечная (для отображения графика, заданного парами значений).
-
Так как диапазон ячеек был выделен заранее, мастер диаграмм автоматически определяет расположение рядов данных. Убедитесь, что данные на диаграмме выбраны правильно. На вкладке Ряд в поле Имя укажите: Результаты измерений. Щелкните на кнопке Далее.
-
Выберите вкладку Заголовки. Убедитесь, что заданное название ряда данных автоматически использовано как заголовок диаграммы. Замените его, введя в поле Название диаграммы заголовок Экспериментальные точки. Щелкните на кнопке Далее.
-
Установите переключатель Отдельном. По желанию, задайте произвольно добавляемого рабочего листа. Щелкните на кнопке Готово.
-
Убедитесь, что диаграмма построена и внедрена на новый рабочий лист, посмотрите ее и щелкните на построенной кривой, чтобы выделить ряд данных.
-
Дайте команду Формат > Выделенный ряд. Откройте вкладку Вид.
-
На панели Линия откройте палитру Цвет и выберите красный цвет. В списке Тип линии выберите пунктир.
-
На панели Маркер выберите в списке Тип маркера треугольный маркер. В палитрах Цвет и Фон выберите зеленый цвет.
-
Щелкните на кнопке Ok, снимите выделение с ряда данных и посмотрите, как изменится вид графика.
-
Сохраните рабочую книгу.
Таблица 6 Пример построения экспериментального графика (график построен на том же листе).
|
|
A |
B |
|
1 |
21,00 |
2 |
|
2 |
20,50 |
4 |
|
3 |
20,00 |
4 |
|
4 |
19,50 |
3 |
|
5 |
19,00 |
5 |
|
6 |
18,50 |
6 |
|
7 |
18,00 |
1 |
|
8 |
17,50 |
1 |
|
9 |
17,00 |
3 |
|
10 |
16,50 |
5 |
|
11 |
16,00 |
7 |
|
12 |
15,50 |
5,8 |
|
13 |
15,00 |
1 |
|
14 |
14,50 |
4 |
|
15 |
14,00 |
2 |
|
16 |
13,50 |
1 |
|
17 |
13,00 |
3 |
|
18 |
12,50 |
5 |
|
19 |
12,00 |
2 |
|
20 |
11,50 |
6 |
|
21 |
11,00 |
7 |
|
22 |
10,50 |
4 |
|
23 |
10,00 |
9 |
|
|
А |
В |
С |
|
1 |
x |
sin |
cos |
|
2 |
0 |
0 |
1 |
|
3 |
10 |
0.17365 |
0.98481 |
|
4 |
20 |
0.34202 |
0.93969 |
|
5 |
30 |
0.5 |
0.86603 |
|
6 |
40 |
0.64279 |
0.76604 |
|
7 |
50 |
0.76604 |
0.64279 |
|
8 |
60 |
0.86603 |
0.5 |
|
9 |
70 |
0.93969 |
0.34202 |
|
10 |
80 |
0.98481 |
0.17365 |
|
11 |
90 |
1 |
6.1E-17 |
|
12 |
100 |
0.98481 |
-0.1736 |
|
13 |
110 |
0.93969 |
-0.342 |
|
14 |
120 |
0.86603 |
-0.5 |
|
15 |
130 |
0.76604 |
-0.6428 |
|
16 |
140 |
0.64279 |
-0.766 |
|
17 |
150 |
0.5 |
-0.866 |
|
18 |
160 |
0.34202 |
-0.9397 |
|
19 |
170 |
0.17365 |
-0.9848 |
|
20 |
180 |
1.2E-16 |
-1 |
|
21 |
190 |
-0.1736 |
-0.9848 |
|
22 |
200 |
-0.342 |
-0.9397 |
|
23 |
210 |
-0.5 |
-0.866 |
|
24 |
220 |
-0.6428 |
-0.766 |
|
25 |
230 |
-0.766 |
-0.6428 |
|
26 |
240 |
-0.866 |
-0.5 |
|
27 |
250 |
-0.9397 |
-0.342 |
|
28 |
260 |
-0.9848 |
-0.1736 |
|
29 |
270 |
-1 |
-2E-16 |
|
30 |
280 |
-0.9848 |
0.17365 |
|
31 |
290 |
-0.9397 |
0.34202 |
|
32 |
300 |
-0.866 |
0.5 |
|
33 |
310 |
-0.766 |
0.64279 |
|
34 |
320 |
-0.6428 |
0.76604 |
|
35 |
330 |
-0.5 |
0.86603 |
|
36 |
340 |
-0.342 |
0.93969 |
|
37 |
350 |
-0.1736 |
0.98481 |
|
38 |
360 |
-2E-16 |
1 |
Построить
точечные диаграммы функций
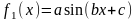 ,
,
 где a,b,c
– произвольные значения, первоначально
равные 1, 1, 0. Аргумент функции x
изменяется то 0º до 360º с интервалом
10º.
где a,b,c
– произвольные значения, первоначально
равные 1, 1, 0. Аргумент функции x
изменяется то 0º до 360º с интервалом
10º.
-
В первой строке задаем названия столбцов (См. Таблица 8).
-
В столбце D задаем имена констант, а в столбце С – их значения
|
|
D |
E |
|
1 |
a |
1 |
|
2 |
b |
1 |
|
3 |
c |
0 |
|
4 |
инт |
10 |
-
В столбец A заносим значения аргумента (A2 0; начиная с A3 записываем формулу, используя абсолютный адрес ячейки - =A2+$E$4 и копируем эту формулу до получения конечного значения аргумента).
-
В столбце B вычисляем функцию f1 относительно x:
=$E$1*($E$2*sin(радианы(A2)+$E$3)
-
В столбце C вычисляем функцию f2 относительно x:
=$E$1*($E$2*cos(радианы(A2)+$E$3)
-
Выделяем таблицу из трех столбцов (A, B, C, начиная с первой строки). Строим график по данным функции на том же листе.

Рис. 4 Точечные диаграммы функций.
-
Запись функций, приятая в математике
Запись функций, приятая в Excel
2sinx
sin(x)
lnx
ln(x)
lgx
log10(x)
ex
exp(x)
xn
x^n
tgx
tan(x)
|x|
abs(x)
π
=пи()
Самостоятельная работа3
|
1. |
|
|
2. |
|
|
3. |
|
|
4. |
|
|
5. |
|
|
6. |
|
|
7. |
|
|
8. |
|
|
9. |
|
|
10. |
|
Построение графика функции с двумя переменными.
Построим
график функции
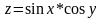 .
.
-
В столбец B (начиная с ячейки B3)– заносим значения переменной y.
-
В строку 2 (начиная с ячейки C2) – заносим значения переменной x.
-
В ячейку C3 – введем формулу, таким образом, чтобы значение переменной y бралось из столбца B, а значение переменной x – из строки 2
=sin(С$2)*cos($B3)
-
Скопируем формулу по строке 2, по всем значениям.
-
Скопируем строку 2 по высоте столбца B со значениями y.
-
Выделим диапазон полученных значений функции и построим поверхность, используя мастер диаграмм (Рис. 5).
Таблица 9 Построение графика функции с двумя переменными.
|
|
A |
B |
C |
D |
E |
F |
G |
H |
I |
|
|
1 |
|
|
x |
|
|
|
|
|
|
|
|
2 |
|
|
-3.00 |
-2.85 |
-2.70 |
-2.55 |
-2.40 |
-2.25 |
-2.10 |
|
|
3 |
y |
2.00 |
0.059 |
0.120 |
0.178 |
0.232 |
0.281 |
0.324 |
0.359 |
|
|
4 |
|
2.15 |
0.077 |
0.157 |
0.234 |
0.305 |
0.370 |
0.426 |
0.472 |
|
|
5 |
|
2.30 |
0.094 |
0.192 |
0.285 |
0.372 |
0.450 |
0.518 |
0.575 |
|
|
6 |
|
2.45 |
0 |
0.221 |
0.329 |
0.430 |
0.520 |
0.599 |
0.665 |
|
|
7 |
|
2.60 |
0.121 |
0.246 |
0.366 |
0.478 |
0.579 |
0.667 |
0.740 |
|
|
8 |
|
2.75 |
0.130 |
0.266 |
0.395 |
0.515 |
0.624 |
0.719 |
0.798 |
|
|
9 |
|
2.90 |
0.137 |
0.279 |
0.415 |
0.541 |
0.656 |
0.755 |
0.838 |
|
|
10 |
|
3.05 |
0.141 |
0.286 |
0.426 |
0.555 |
0.673 |
0.775 |
0.860 |
|
|
11 |
|
3.20 |
0.141 |
0.287 |
0.427 |
0.557 |
0.674 |
0.777 |
0.862 |
|
|
12 |
|
3.35 |
0.138 |
0.281 |
0.418 |
0.546 |
0.661 |
0.761 |
0.845 |
|
|
13 |
|
3.50 |
0.132 |
0.269 |
0.400 |
0.522 |
0.633 |
0.729 |
0.808 |
|
|
14 |
|
3.65 |
0.123 |
0.251 |
0.373 |
0.487 |
0.590 |
0.680 |
0.754 |
|
|
15 |
|
3.80 |
0.112 |
0.227 |
0.338 |
0.441 |
0.534 |
0.615 |
0.683 |
|
|
16 |
|
3.95 |
0.097 |
0.199 |
0.295 |
0.385 |
0.467 |
0.537 |
0.596 |
|
|
17 |
|
4.10 |
0.081 |
0.165 |
0.246 |
0.321 |
0.388 |
0.447 |
0.496 |
|
|
18 |
|
4.25 |
0.063 |
0.128 |
0.191 |
0.249 |
0.301 |
0.347 |
0.385 |
|
|
19 |
|
4.40 |
0.043 |
0.088 |
0.131 |
0.171 |
0.208 |
0.239 |
0.265 |
|
|
20 |
|
4.55 |
0.023 |
0.046 |
0.069 |
0.090 |
0.109 |
0.126 |
0.140 |
|
|
21 |
|
4.70 |
0.002 |
0.004 |
0.005 |
0.007 |
0.008 |
0.010 |
0.011 |
|
|
22 |
|
4.85 |
-0.019 |
-0.039 |
-0.059 |
-0.077 |
-0.093 |
-0.107 |
-0.118 |
|
|
24 |
|
5.00 |
-0.040 |
-0.082 |
-0.121 |
-0.158 |
-0.192 |
-0.221 |
-0.245 |
Рис. 5 Построение графика поверхности.
Самостоятельная работа.
Построить график функций.
|
1 |
|
|
2 |
|
|
3 |
|
|
4. |
|
|
5. |
|
|
6. |
|
|
7. |
|
|
8. |
|
|
9. |
|
|
10. |
|
Excel. Операции с матрицами.
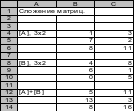
Сложение двух матриц.
Складывать матрицы можно только при условии, что они имеют одинаковый размер.
Чтобы сложить две матрицы, нужно сложить все их соответствующие элементы.
-
В ячейку B12 записать формулу =B4+B8.
-
Скопировать содержимое ячейки в диапазон ячеек B12:B14.
Результат на Рис. 6.
Умножение матрицы на скаляр.
Чтобы умножить матрицу на скаляр, нужно умножить на скаляр каждый элемент матрицы.
-
Введем в ячейки электронной таблицы скаляр, представляющий собой константу и матрицу B4:C6, которую нужно умножить на него.
-
В ячейку B9 введем формулу =$B$3*B4.
-
Копируем формулы из ячейки B9 в диапазон B9:C11.
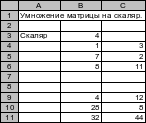
Рис. 7 Умножение матрицы на скаляр.
Перемножение матриц.
Две матрицы можно перемножить при условии, что количество столбцов первой матрицы равно количеству строк второй матрицы. («Внутренние» размеры матрицы должны совпадать, размеры результирующей матрицы состоят из «внешних» размеров).
-
Ввести матрицу 3х2 (произвольные числа) в ячейки A4:B6.
-
В ячейки A9:A10 ввести матрицу 2х1 (произвольные числа).
-
Выделить ячейки C4:C6.
-
В строке функций набрать формулу =МУМНОЖ(A4:B6;A9:A10).
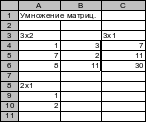
Рис. 8 Умножение матриц.
Транспонирование матриц.
Чтобы транспонировать любую матрицу, нужно поменять ее строки и столбцы. В Excel это можно сделать двумя способами. Рассмотрим оба метода.
С помощью команды меню «Специальная вставка»
-
Введите исходную матрицу.
-
Выделите ячейки, в которых содержатся эта матрица.
-
Скопируйте их содержимое в буфер обмена.
-
Установите указатель мыши на ячейку, в которой будет содержаться верхнее левое значение транспонированной матрицы.
-
Нажмите правую кнопку мыши, выбрать из выпадающего меню Специальная вставка.
-
Отобразится диалоговое окно Специальная вставка.
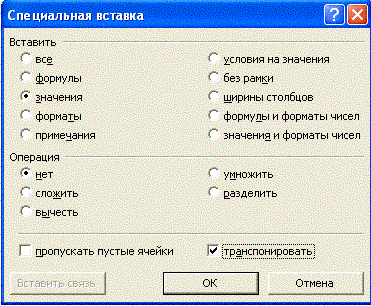
Рис. 9 Окно «Специальная вставка»
-
На панели Вставить установите переключатель в положение значение и установите флажок транспонировать, расположенный в нижней части диалогового окна.
-
Нажмите OK.
С помощью функции массива.
-
Введите исходную матрицу.
-
Укажите, куда нужно поместить результат (выделите диапазон ячеек).
-
В окне формул введите функцию =ТРАНСП(матрица).
-
Укажите с помощью мышки диапазон, в котором содержится матрица.
-
Завершите функцию нажатием клавиш CTRL+SHIFT+ENTER.
Задание.
Транспонируйте обоими способами приведенные ниже матрицы.
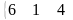


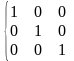
Обращение матриц.
Операция обращения матриц применима только к квадратным матрицам. Однако не для каждой матрицы существует обратная к ней матрица. Чтобы матрицу можно было обратить, она должна быть несингулярной. (детерминант матрицы должен быть отличен от 0).
Детерминант матрицы – это скалярная величина, которая вычисляется на основе всех матричных элементов и часто используется при решении систем уравнений.
Для вычисления детерминанта в Excel используется функция массива =МОПРЕД(матрица). Если он отличен от 0, то матрицу можно обратить.
-
Введите матрицу, которую нужно обратить.
-
Вычислите ее детерминант. Если он не равен 0 – продолжите процесс обращения, иначе измените исходные данные.
-
Укажите место для размещения обратной матрицы и ее правильный размер - он совпадает с размером исходной матрицы.
-
Начните вводить функцию массива =МОБР(матрица) и укажите с помощью мыши ячейки, в которых содержится обращаемая матрица.
-
Нажмите сочетание клавиш CTRL+SHIFT+ENTER.
Решение систем линейных уравнений.
Дана система линейных уравнений:
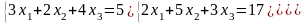
-
Запишем матрицу коэффициентов в таблицу.
-
Запишем столбец из констант, стоящих в правой части уравнений.
-
С помощью функции МОБР() найдем обратную матрицу, матрице коэффициентов.
-
Умножим обратную матрицу на столбец констант и получим значения неизвестных.
-
Решение получено.

Самостоятельная работа.
Определить детерминант матрицы и решить (если это возможно) системы линейных уравнений.

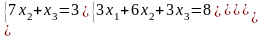
Список литературы.
-
«Инженерные расчеты в Excel». Рональд У. Ларсен. Издательский дом «Вильямс», Москва, 2002.
-
«Подробное руководство по созданию формул в Excel 2002». Джон Уокенбах. «Диалетика», Москва, 2002.
-
“Новейший самоучитель работы на компьютере» под редакцией С.Симоновича. ДЕСС INFORMCOM PRESS. Москва 2010
1 Итоговые функции являются продолжением Таблицы 4.
2 Под аргументом функции (x) может быть выражение, состоящее из некоторых функций.
3 Количество значений аргумента функции для всех заданий равно 40. Проанализировать, что происходит с графиками функций при изменении константы. Константа – а – произвольное число.

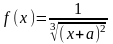 ,
где
,
где 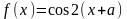 ,
где
,
где 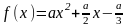 ,
где
,
где 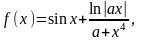 где
где
 где
где  где
где 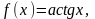 где
где  где
где  ,
где
,
где 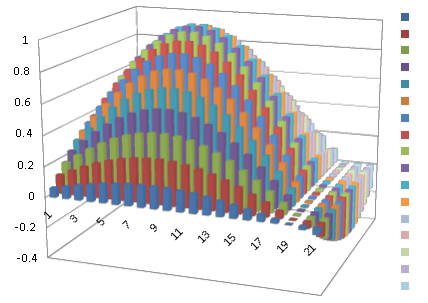 .109
.109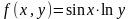 ,
где
,
где 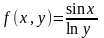 ,
где
,
где 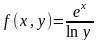 ,
где
,
где 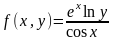 ,
где
,
где 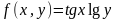 ,
где
,
где 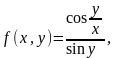 где
где  где
где 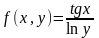 где
где 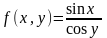 где
где 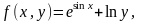 где
где