Файл: Средства создания программ, выполняемых на стороне сервера (АНАЛИЗ ЭТАПОВ ПРОЕКТИРОВАНИЯ ПРОГРАММ).pdf

где С – числовая матрица, содержащая значения емкостей и индуктивностей схемы, R – матрица резистивных сопротивлений, - вектор, содержащий искомые величины напряжения в узлах и токов в ветвях схемы, - вектор, содержащий входные сигналы.

Требуется найти вектор . Для решения поставленной задачи идеально подойдет явный метод Эйлера (20), который получается путем разложения решения уравнения в ряд Тейлора в пределах точки t [7]:

- подвектор значений напряжений в узлах, подключенных к конденсаторам;

- подвектор значений сил токов через катушки индуктивности;

- подвектор значений напряжений в узлах, не подключенных к конденсаторам.

Составленная макромодель (22) можно переписать в вид:

Исключив из макромодели подвектор получим:

Ввиду того, что матрица является диагональной, а друггеи подматрицы разрежены, то можно получить вторую макромодель [8]:

Учитывая, что – диагональные матрицы, запишем модель в виде системы дифференциальных уравнений, заданной в явной форме:

В следующем подразделе будет произведен обзор статей зарубежных инженер, которые разработали свои методы получения макромодели электрической схемы и произведи временной анализ полученных результатов.

На тему построения макромоделей электрических схем опубликовано огромное количество исследований, предоставляющие различные решения для устранения поставленной проблемы. На сегодняшний день исследования в этой области не проводятся, нет новых подходов к решению задачи сокращения количества элементов в схеме, поэтому необходимо детально изучить исследования прошлого века. Наиболее распространенным алгоритмом является PRIMA [1], который получает макромодели уменьшенного порядка для линейных пассивных электрических схем.

Авторы утверждают, что алгоритм блока Арнольди [10], лежащий в основе метода PRIMA, создает векторы, используемые для реализации преобразований в матрицах MNA (модифицированный узловой анализ, позволяющий упростить представление компонентов схемы в узловом анализе, а частности для первого закона Кирхгофа) [11]. Однако, у данного подхода имеется ограничение: преобразования полученных макромоделей для RLC-схем должны быть конгруэнтными. Этот метод гарантирует пассивность схемы RLC, обеспечивая при этом высокую степень точности.

В этом исследовании авторы сравнивают разработанный подход с методом MPVL (MatrixPadé через Lanczos) [12] и пришли к выводу, что алгоритмы скомпенсированы с точки зрения точности. Аналогично, и с методом, использующим в своей основе уравнения Ляпунова. Эти методы не могут гарантировать пассивность электрической схемы, что может отрицательно повлиять на анализ во временной и функциональной областях схемы.

Помимо математического объяснения достижения цели, авторы выполняют временное моделирование макромоделей в области Spice, чтобы проверить эффективность метода несколькими способами. Однако подход авторов является неполным, поскольку по мере увеличения количества входящих элементов схемы точность расчетов уменьшается.

2.2 Выбор среды проектирования программ

В данной главе будет описан выбор среды моделирования электрической схемы, необходимой для проведения упрощения электрической схемы. На данный момент существует огромный спектр различных по управлению и функционалу систем автоматизированного проектирования САПР. Наиболее известными считаются такие программы аналогового и цифрового моделирования, как Micro-CAP, NI Multisim и LTspice. Ниже представлены вид графического функционала перечисленных симуляторов моделирования работы цифровых и аналоговых электрических цепей (Рис. 7 – 9).

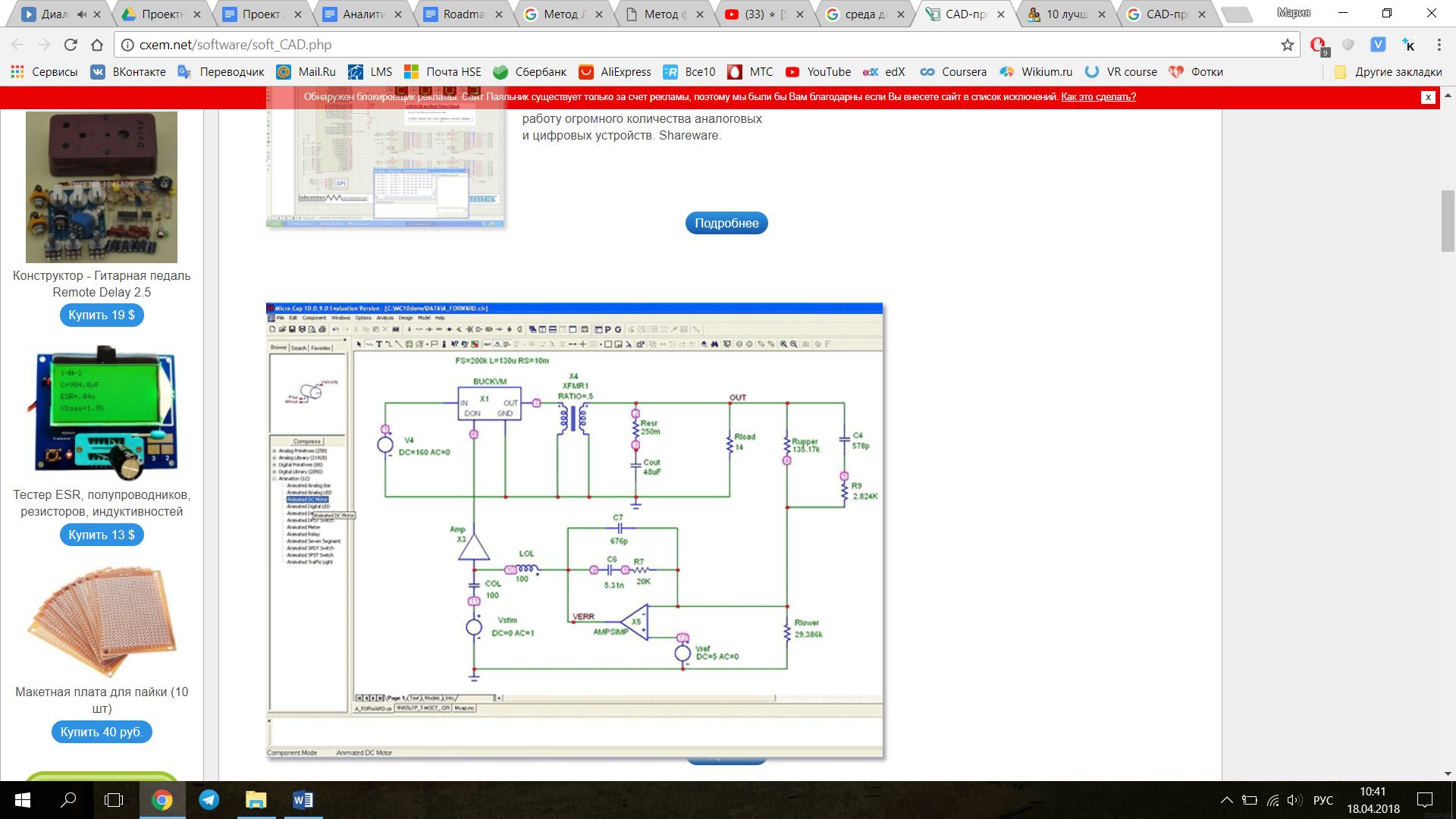
Рис. 7. Среда Micro-CAP

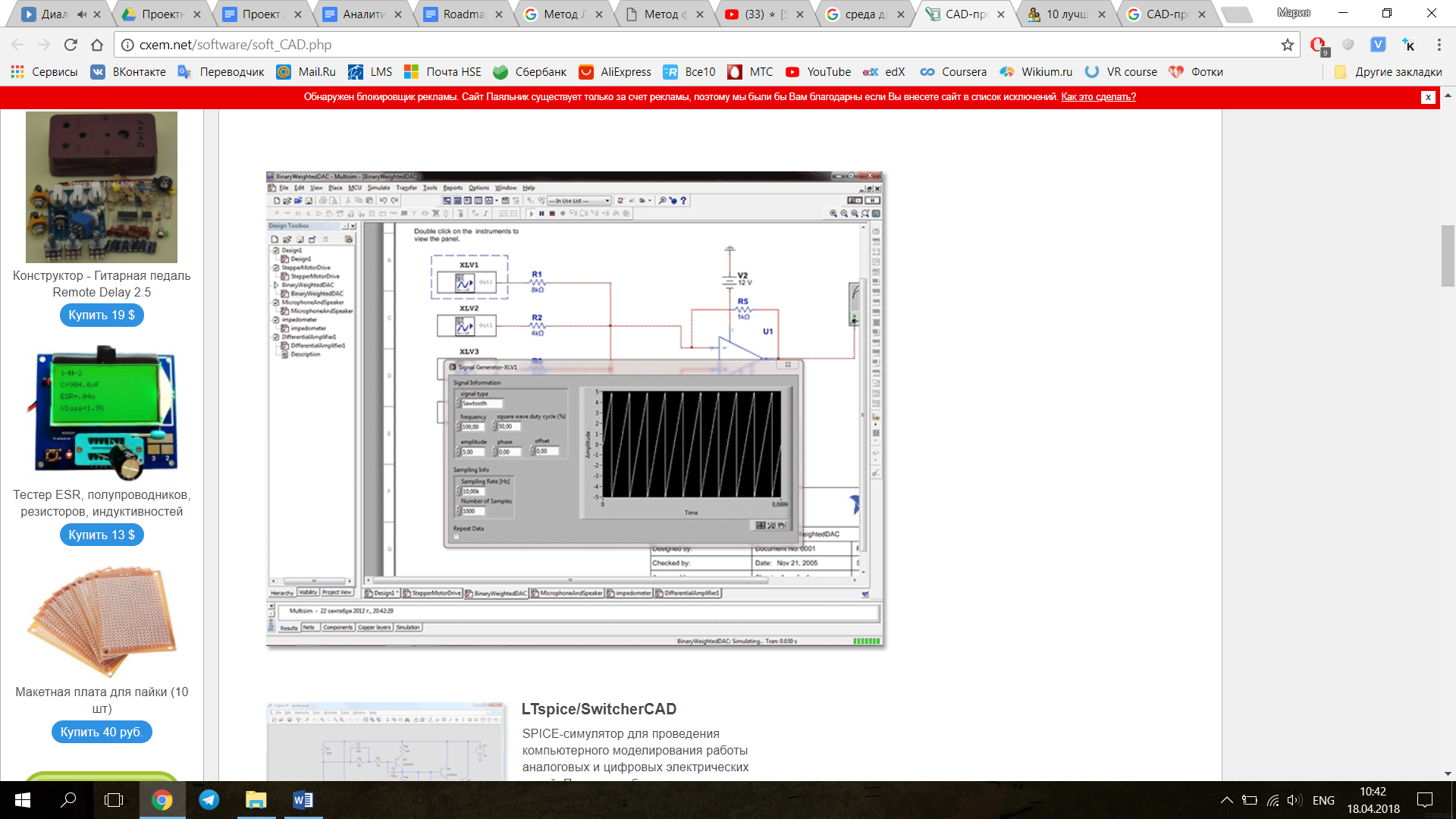
Рис. 8. Среда NI Multisim

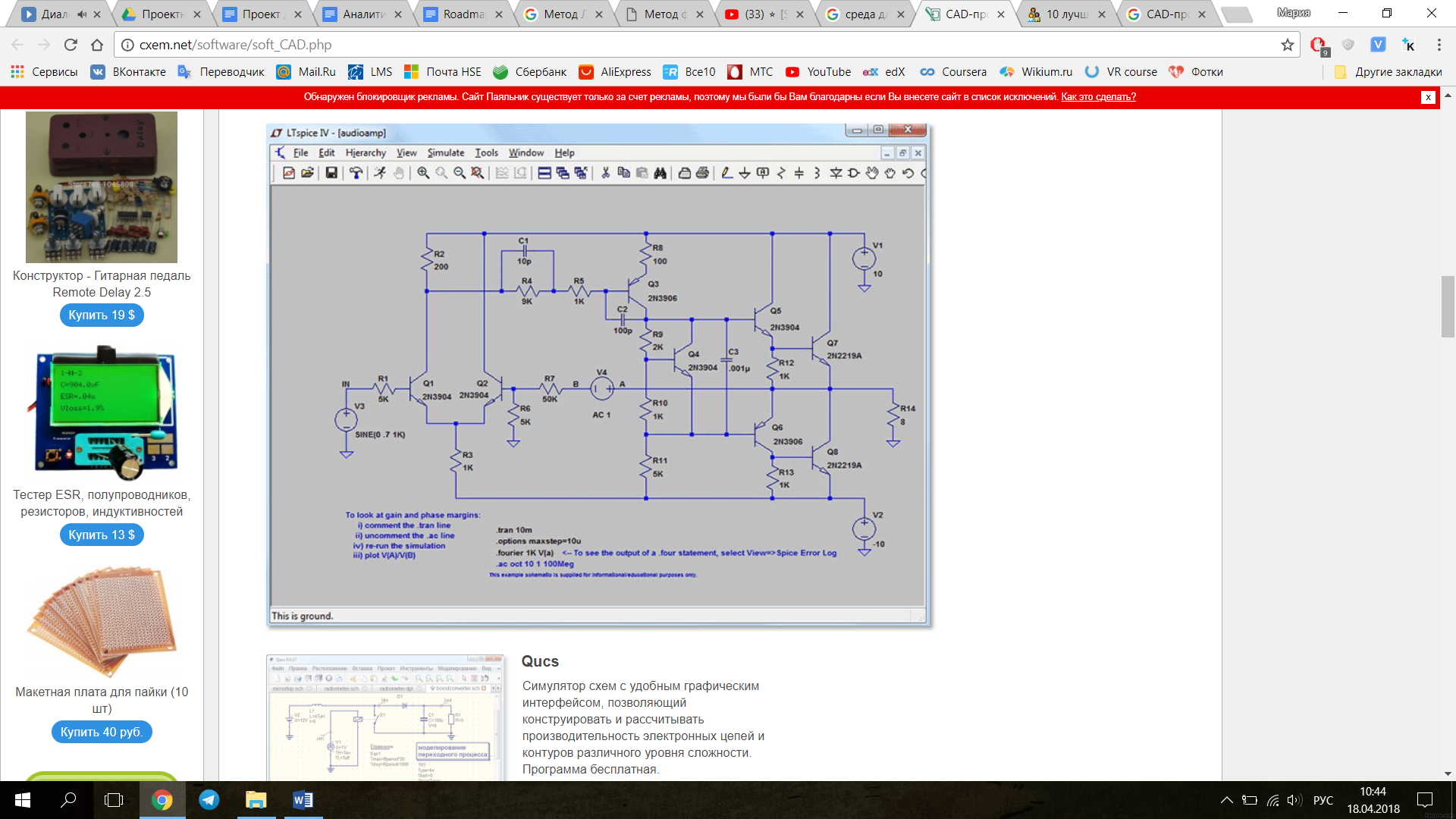
Рис. 9. Среда LTSpice

Представленные среды для симуляции работы электрических схем имеют схожий функционал, предоставляются бесплатно и просты в синтезе схемы и ее последующем моделировании. Поэтому решение выбора среды было принято исходя лишь из личных предпочтений и раннему опыту работы в одной из представленных программ. Последующий синтез электрических схем будет производиться в среде LTSpice [9].

Стоит разобраться, для чего нужна среда для создания электрической схемы. В LTspice синтезируемая схема хранится в текстовом asc-файле, в котором каждому созданному компоненту цепи соответствует строка, описывающая его расположение, а именно между какими функциональными узлами он находится, номинальное значение и прочие параметры. На рисунке 10 представлен вид файла, хранящего модель идеального трансформатора.

Рис. 10. Вид файла, хранящего модель трансформатора

Исходя из этого файла нетрудно составить матрицу емкостей, сопротивлений и индуктивностей, требуемую в макромодели. В разрабатываемый программный модуль будет подаваться электрическая схема из среды LTspice в качестве asc-файла, который в последствии будет преобразован к матричному виду. В главе 3 более подробно описаны требуемые для макромоделирования типы матриц, помимо компонентных матриц, необходимо составить вектор со входными значениями.

2.3 Разработка программного модуля

В качестве среды для разработки программного модуля построения макромоделей электрической схемы выбран QtCreator. Это кроссплатформенная IDE (интегрированная среда разработки) со свободным программным обеспечение для разработки приложений с помощью таких языков программирования, как C/C++.

Данная среда разработки выбрана благодаря своему удобству, простоте использования и широкому набору предоставляемых форм для создания пользовательского интерфейса.

Разработанный программный модуль представлен на рисунке 11. Далее будет описаны его функциональные возможности. Для построения макромодели электрической схемы пользователю требуется загрузить в систему asc-файл. Сделать это можно нажав на кнопку «Открыть файл». После этого в поле «Выберите метод макромоделирования» необходимо указать, каким именно методом упрощения пользователь хотел бы воспользоваться.

Рис. 11. Окно программы «Модуль построения макромоделей электрических схем»

В случае если, пользователю захочется получить сведения о том или ином методе, требуется нажать кнопку «О методе», после чего в новом окне появится подробное описание интересующего метода макромоделирования. Указав два этих главных параметра, а именно, файл со схемой и алгоритм построения макромодели, необходимо нажать кнопку «Рассчитать». После нажатия этой кнопки в сравнительной таблице внизу отобразится количество каждого из видов пассивных элементов до и после применения метода упрощения.

ЗАКЛЮЧЕНИЕ

В ходе выполнения данной работы был разработан программный модуль построения макромоделей электрических схем. Данный модуль имеет широкий спектр областей применения, начиная с обучающей программы по схемотехнике и математике, и заканчивая разработкой электронных устройств и космических аппаратов. С его помощью можно решать такие существенные вопросы, как распознавание наиболее подверженной к возникновению тока короткого замыкания области, расположенной на поверхности космического летательного аппарата. Стоит отметить, что это довольно узкоспециализированная задача, и помимо нее, разработанная программа может применена при разработке электронного устройства на этапе проектирования принципиальной схемы для сокращения количества составных элементов в схеме, что обеспечит увеличение скорости работы устройства и уменьшит стоимость компонентов, и соответственно, себестоимость продукта. Однако, наиболее успешным образом разработанный программный модуль найдет свое применение в сфере академического обучения учеников старших классов и студентов младших курсов технических специальностей базовым алгоритмам и методам макромоделирования, иными словами, нахождения систем интегро-дифференциальных уравнений с наибольшей степенью точности и наименьшими затратами компьютерных ресурсов, необходимых для расчета такой системы.

Разработка программы началась с определения понятия макромодели и ее применения в области электротехники. Макромодель представляет собой математического описание значений напряжений в функциональных узлах электрической схемы и сил тока в ветвях, рассчитанных с достаточной степенью точности. Трудность решения задачи макромоделирования состоит в том, что нахождение решений системы дифференциальных уравнений, полученных на основании имеющейся схемы, занимает много процессорного времени и памяти, вычисление таких систем может затянуться на несколько часов, в случае электрической схемы, содержащей более сотни тысяч функциональных узлов.

После это была определена компонентная база, из которой будут строиться макромодели. В качестве используемых элементов были выбраны пассивные элементы, такие как резисторы, конденсаторы и катушки индуктивности. Выбор соответствующей компонентной основы вызван тем, что большинство электронных полупроводников элементов могут быть с различной степенью точности представлены через эти компоненты.

Следующим этапом разработки был обзор методов построения математического представления электрической схемы. Существует два основных подхода: аналитическое решение системы и составление системы искомых сил тока и напряжений с помощью законов Кирхгофа, или же составление электрической схемы в среде, предназначенной для синтеза и моделирования работы схем, выбор режима моделирования. Среда моделирования строит матрицы на основе функциональных узлов для емкостей, индуктивностей и резисторов, после чего решает матричное дифференциальное уравнение методом Рунге-Кутты. Однако, этот метод решения является неэффективных, поэтому было принято решение применять другие методы нахождения решения дифференциальных уравнений. В рамках данной работы были рассмотрены такие методы, как явный и неявный метод Эйлера, метод PRIMA, основанный на алгоритме Арнольди, а также метод Крылова.

Завершающим этапом была разработка пользовательского интерфейса, отражающий результаты применения методов сокращения количества элементов в схеме. На вход программа принимает сгенерированную схему в среде LTspice в формате asc-файла и метод макромоделирования из списка предложенных. После выполнения расчетов в сравнительной таблице внизу отображается количество элементов в схеме до и после применения метода. Также программа предоставляется справочную информацию о каждом из методов макромоделирования.

В качестве дальнейшей разработки данный программный модуль может быть функционально расширен. Допустимо добавление других методов макромоделирования, возможности синтезировать электрические схемы из других систем, не только LTspice, но наиболее важной доработкой модуля будет возможность применения методов не только к схемам, содержащим пассивные элементы, но и к любой схеме в принципе.

СПИСОК ЛИТЕРАТУРЫ

1. Odabasioglu A., Celik M., L. T. Pillage, “PRIMA: Passive reduced-order interconnect macromodeling algorithm,” IEEE Trans. Computer-Aided Design, pp. 645–654, Aug. 1998.
2. Гуревич Г.С., Каневский С.Н. Индукция, взаимоиндукция, самоиндукция - это просто. Теория абсолютности. М.: У Никитских ворот, 2015.
3. Лаврентьев Б.Ф. Схемотехника электронных средств. М.: Академия, 2010. С. 53—68.
4. Ebers J. J., Moll J. L. Large-signal behavior of junction transistors // Proceedings of the Institute of Radio Engineers. — 1954. — Vol. 42, № 12. — P. 1761–72.
5. Демидович Б.П. (ред) Задачи и упражнения по математическому анализу для ВТУЗов. М.: Астрель, 2004.
6. Эйлер Л. Интегральное исчисление, том 1, раздел 2, гл. 7. М.: Государственное издательство технико-теоретической литературы, 1956.
7. Востриков А.В. Приближенный метод расчета растекания токов по элементам конструкции космического аппарата при электростатических разрядах. − Технологии ЭМС,2010.−№2(33).−С.75−79.
   Востриков А.В., Борисов Н.И. Новый алгоритм построения макромоделей на основе методов Эйлера. Труды XXI Международного совещания «Радиационная физика твердого тела», 22 августа – 27 августа 2011 г. Севастополь. − С. 283−291.
8. LTspice: modeling circuits [Электронный ресурс]. – Режим доступа: http://forum.cxem.net/applications/core/interface/file/attachment.php?id=394136 (дата обращения: 03.05.18).
9. K. J. Kerns, A. T. Yang. “Stable and efficient reduction of large, multiport RC networks by pole analysis via congruence transforms,” IEEE Trans. Computer-Aided Design Integr. Circuits Syst., vol. 16, no. 7, pp. 734–744, Jul. 1997.
   1. Odabasioglu, M. Celik, L. T. Pillage. “Practical considerations for passive reduction of RLC circuits,” in Proc. Int. Conf. Computer Aided-Design, San Jose, CA, Nov. 1999, pp. 214–219.
10. P. Feldmann and R. W. Freund, “Efficient linear circuit analysis by Padé approximation via the Lanczos process,” IEEE Trans. Computer-Aided Design Integr. Circuits Syst., vol. 14, no. 5, pp. 639–649, May 1995.
11. J.-R. Li, F. Wang, and J. White, “An efficient lyapunov equation-based approach for generating reduced-order models of interconnect,” in Proc. 36th ACM/IEEE Design Automation Conf., New Orleans, LA, Jun. 1999, pp. 1–6.
12. Macromodeling Program [Электронный ресурс]. – Режим доступа: https://github.com/Macromodeling (дата обращения: 10.06.2019).