Добавлен: 19.10.2018
Просмотров: 1039
Скачиваний: 6

Задание 4 Построение графиков
параметрически заданных функций
Значения параметра t (или
), а также переменных x и y
располагать в столбцах. Значения параметра вычислить в
указанных пределах с указанным шагом. Если имеются точки
разрыва, то их присутствие в таблице обязательно.
Все имеющиеся
константы вынести в отдельные ячейки
. В
формулах использовать абсолютные ссылки на ячейки с
константами.
Вычислить значения переменных x и y попарно для каждой
константы (или набора констант).
Построить графики зависимостей Y(x) для каждой константы
отдельно
.
В легенде для каждого графика указать значение константы.
График должен иметь название, соответствующее названию
кривой (дано в каждом варианте).
Для каждого графика:
назначить цвет заливки области диаграммы, области
построения диаграммы,
выделить жирной линией оси,
дать название осям координат
показать сетку
При сдаче уметь:
построить диаграмму,
добавлять или удалять дополнительные элементы
диаграммы (легенда, сетка, названия, подписи данных)
изменять форматирование всех элементов диаграммы
изменять расположение диаграммы.

Вариант 1.
Построить 5 графиков функций отдельно.
Уравнения
циклоиды
заданы в параметрическом виде:
)
cos
1
(
)
sin
(
t
a
y
t
t
a
x
,
где t меняется от 0 до
6
с шагом 0,1.
a
= 1,0, 1,25, 1,5, 1,75, 2,0.
Вариант 2.
Построить 6 графиков функции отдельно.
Уравнение кривой
«Локон Аньези»
)
(
2
2
3
x
a
a
y
,
где x меняется от –6 до 6 с шагом 0,1.
a
= 1,2,3,4,5,6.
Вариант 3.
Построить 6 графиков функции отдельно.
Уравнения кривой
«Декартов лист»
заданы в параметрическом
виде:
)
1
(
3
,
)
1
(
3
3
2
3
t
at
y
t
at
x
,
где t меняется от –6 до 6 с шагом 0,1, кроме точки t=-1.
a
=1,2,3,4,5,6.

Вариант 4.
Построить 6 графиков функции отдельно.
Уравнения
циссоиды
заданы в параметрическом виде
:
2
3
2
2
1
,
1
t
at
y
t
at
x
,
где t изменяется от –6 до 6 с шагом 0,1.
a
=1,2,3,4,5,6.
Вариант 5.
Построить 6 графиков функции отдельно.
Уравнения
строфоиды
заданы в параметрическом виде:
1
)
1
(
,
1
)
1
(
2
2
2
2
t
t
at
y
t
t
a
x
,
где t изменяется от –6 до 6 с шагом 0,1.
a
=1,2,3,4,5,6.
Вариант 6.
Построить 6 графиков функции отдельно.
Уравнения
кривой
«Конхоида
Никомеда»
заданы
в
параметрическом виде:
t
b
t
a
y
t
b
a
x
sin
tan
cos
,
где t изменяется от
)
2
05
,
0
(
до
)
05
,
0
2
3
(
с шагом 0,05, кроме
точки
2
.
b=3,
a
=1,2,3,4,5,6.

Вариант 7.
Построить 6 графиков функции отдельно.
Уравнения кривой
«Улитка Паскаля»
заданы в параметрическом
виде:
t
b
t
t
a
y
t
b
t
a
x
sin
sin
cos
cos
cos
2
,
где t изменяется от 0 до
2
с шагом 0,05. b=3,
a
=1,2,3,4,5,6.
Вариант 8.
Построить 6 графиков функции отдельно.
Уравнения
циклоиды
заданы в параметрическом виде:
)
cos
1
(
)
sin
(
t
a
y
t
t
a
x
,
,где t изменяется от 0 до
6
с шагом 0,1.
a
=2,
=0,4; 0,7; 1,0; 1,3; 1,6; 2,0.
Вариант 9.
Построить 6 графиков функции отдельно.
Уравнения
эпициклоиды
заданы в параметрическом виде:
]
)
(
sin[
sin
)
(
]
)
(
cos[
cos
)
(
a
b
a
a
b
a
y
a
b
a
a
b
a
x
,где
изменяется от 0 до
2
с шагом 0,05.
b=1,2,3,4,5,6.
a
=1.
Вариант 10.
Построить 6 графиков функции отдельно.
Уравнения
эпициклоиды
заданы в параметрическом виде:
]
)
(
sin[
sin
)
(
]
)
(
cos[
cos
)
(
a
b
a
a
b
a
y
a
b
a
a
b
a
x
,где
изменяется от 0 до
6
с шагом 0,1.
b=1,2,3,4,5,6.
a
=5.
Вариант 11.
Построить 4 графика функции отдельно.
Уравнения
эпициклоиды
заданы в параметрическом виде:
]
)
(
sin[
sin
)
(
]
)
(
cos[
cos
)
(
a
b
a
a
b
a
y
a
b
a
a
b
a
x
,где
изменяется от 0 до
6
с шагом 0,1.
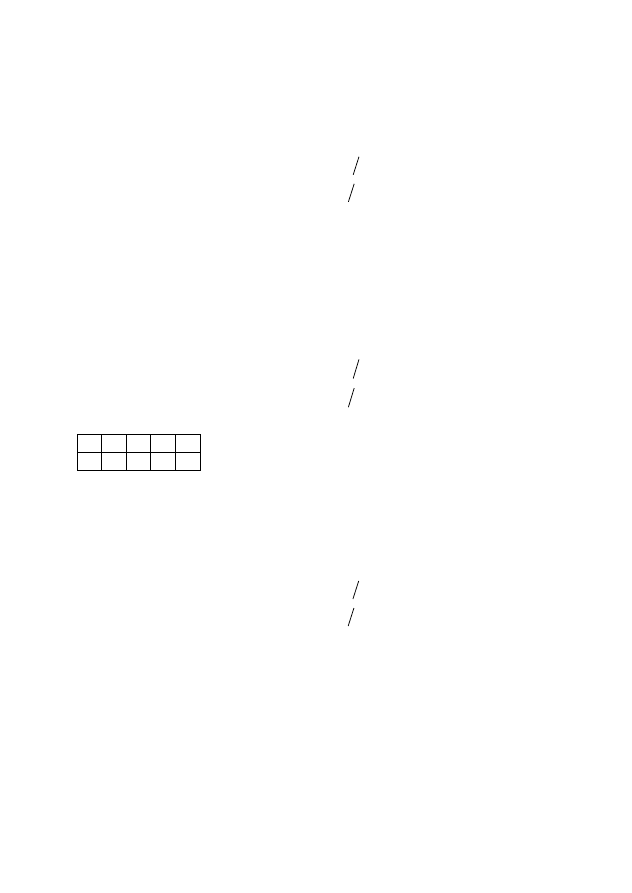
a 2 3 5 7
b 7 5 3 2
Вариант 12.
Построить 6 графиков функции отдельно.
Уравнения
гипоциклоиды
заданы в параметрическом виде:
]
)
(
sin[
sin
)
(
]
)
(
cos[
cos
)
(
a
a
b
a
a
b
y
a
a
b
a
a
b
x
,где
изменяется от 0 до
2
с шагом 0,05.
b=2,3,4,5,6,11.
a
=1.