Файл: 2.3. Термины и определения системного анализа и теории систем.docx
ВУЗ: Смоленский областной казачий институт промышленных технологий и бизнеса
Категория: Лекция
Дисциплина: Моделирование систем
Добавлен: 19.11.2018
Просмотров: 1218
Скачиваний: 13
1.2. ОСНОВНЫЕ ПОНЯТИЯ СИСТЕМНОГО АНАЛИЗА
1.2.1. ЗАДАЧИ СИСТЕМНОГО АНАЛИЗА
В процессе создания ИС исследователи стремятся к наиболее полному и объективному представлению объекта автоматизации - описанию его внутренней структуры, объясняющей причинно-следственные законы функционирования и позволяющей предсказать, а значит, и управлять его поведением. Одним из условий автоматизации является адекватное представление системы с управлением в виде сложной системы.
Существует несколько подходов к математическому описанию сложных систем. Наиболее общим является теоретико-множественный подход, при котором система S представляется как отношение S Х х У, где Х и У - входной и выходной объекты системы соответственно.
Точнее говоря, предполагается, что задано семейство множеств Vi, где i I-множество индексов, и система задается на Vi , как некоторое собственное подмножество декартова произведения, все компоненты которого являются объектами системы. Такое определение ориентировано на исследование предельно общих свойств систем независимо от их сущности и лежит в основе общей теории систем.
Другие подходы, сформулированные на более низком уровне общности, не могут претендовать на роль математического фундамента общей теории систем, но позволяют конструктивно описывать системы определенного класса. Так, например, общие закономерности функционирования и свойства систем с управлением являются предметом изучения системного анализа. Принято считать, что системный анализ - это методология решения проблем, основанная на структуризации систем и количественном сравнении альтернатив.
Иначе говоря, системным анализом называется логически связанная совокупность теоретических и эмпирических положений из области математики, естественных наук и опыта разработки сложных систем, обеспечивающая повышение обоснованности решения конкретной проблемы.
В системном анализе используются как математический аппарат общей теории систем, так и другие качественные и количественные методы из области математической логики, теории принятия решений, теории эффективности, теории информации, структурной лингвистики, теории нечетких множеств, методов искусственного интеллекта, методов моделирования.
Применение системного анализа при построении ИС дает возможность выделить перечень и указать целесообразную последовательность выполнения взаимосвязанных задач, позволяющих не упустить из рассмотрения важные стороны и связи изучаемого объекта автоматизации. Иногда говорят, что системный анализ - это методика улучшающего вмешательства в проблемную ситуацию.
В состав задач системного анализа в процессе создания ИС входят задачи декомпозиции, анализа и синтеза.
Задача декомпозиции означает представление системы в виде подсистем, состоящих из более мелких элементов. Часто задачу декомпозиции рассматривают как составную часть анализа.
Задача анализа состоит в нахождении различного рода свойств системы или среды, окружающей систему. Целью анализа может быть определение закона преобразования информации, задающего поведение системы. В последнем случае речь идет об агрегации (композиции) системы в один-единственный элемент.
Задача синтеза системы противоположна задаче анализа. Необходимо по описанию закона преобразования построить систему, фактически выполняющую это преобразование по определенному алгоритму. При этом должен быть предварительно определен класс элементов, из которых строится искомая система, реализующая алгоритм функционирования.
В рамках каждой задачи выполняются частные процедуры. Например, задача декомпозиции включает процедуры наблюдения, измерения свойств системы. В задачах анализа и синтеза выделяются процедуры оценки исследуемых свойств, алгоритмов, реализующих заданный закон преобразования. Тем самым вводятся различные определения эквивалентности систем, делающие возможными постановку задач оптимизации, т. е. задач нахождения в классе эквивалентных систем системы с экстремальными значениями определяемых в них функционалов.
В основе системного анализа как науки лежат определения основных понятий и принципы проведения анализа. Рассмотрим эти понятия.
1.2.2. ПОНЯТИЕ СИСТЕМЫ КАК СЕМАНТИЧЕСКОЙ МОДЕЛИ
Строгого, единого определения для понятия «система» в настоящее время нет. В качестве «рабочего» определения в литературе под системой в общем случае понимается совокупность элементов и связей между ними, обладающая определенной целостностью.
Рассматривая систему относительно построения ИС, более полно это определение можно пояснить на основе понятия модели.
Пусть А и В - два произвольных множества. Функция f, однозначно ставящая в соответствие каждому элементу аА элемент f(а)В, называется отображением множества А в множество В и обозначается как f: АВ .
Элемент f(а) = b называется значением элемента а при отображении f, или образом а; А - область определения, В - область значений отображения f.
Если есть элементы bi В, не являющиеся образом никаких элементов аi А, то отображение f называется отображением «в» В. Если f(А) = В, то отображение f называется отображением «на» В.
Функция f-1(B) - множество элементов из А, образы которых принадлежат В, называется прообразом множества В, т.е. f-1(В) = {а А | f(а) В}.
В общем случае f-1 может не быть отображением «в» или «на» А, так как функция f-1 может быть неоднозначной.
Отображение называется взаимно однозначным, если каждый элемент множества В является образом не более чем одного элемента из А.
Отображение f множества А на (в) В называется гоморфизмом множеств, если выполняется условие (а1, а2, …, аk) (f(а1),f( а2), …,f( аk)), где аiA, f( аi) B.
Изоморфизмом множества А на В взаимно однозначный гоморфизм, т.е. (а1, а2, …, аk) A (f(а1),f( а2), …,f( аk))B.
Введенные понятия позволяют определить модель как изоморфизм А в , где А - множество фиксированных элементов предметной области с исследуемыми связями, отношениями между этими элементами, - абстрактное множество, задаваемое кортежем = <{M}, P1, P2, …., Pn>
где {М}- множество элементов модели, соответствующих элементам предметной области, называемое носителем модели;
P1, P2, …., Pn - предикаты, отображающие наличие того или иного отношения между элементами предметной области.
Предикат - это логическая п-я пропозициональная функция, определенная для предметной области и принимающая значения либо истинности, либо ложности.
Носитель модели является содержательной областью предикатов P1, P2, …., Pn Предикаты называются сигнатурой модели .
Выбор носителя и сигнатуры при построении модели определяется предметом исследования.
Уточним теперь понятие системы, ориентированное на задачи декомпозиции, анализа и синтеза, т.е. на проведение преобразования a b между двумя подмоделями. Системой называется кортеж S = <a , b , Po (a ,b)>, где
a - подмодель, определяющая поведение системы. Иногда эта подмодель может рассматриваться как «черный ящик», о котором известно лишь то, что на определенные воздействия он реагирует определенным образом;
b - подмодель, определяющая структуру системы при ее внутреннем рассмотрении;
Po (a ,b)- предикат целостности, определяющий назначение системы, семантику (смысл) моделей a и b , а также семантику преобразования a b.
Po (a ,b) = 1, если преобразование a b существует при взаимно однозначном соответствии между элементами носителей моделей a и b, в противном случае Po (a ,b)= 0. Наличие предиката целостности позволяет говорить о том, что система -это семантическая модель, имеющая внутреннюю интерпретацию.
Подмодель a
- может быть представлена в виде кортежа,
включающего пять объектов:
![]()
где х = х(t) - входной сигнал, т.е. конечное множество функций времени
t : <xo(t), ... , xk(t)>;
у = у(t) - выходной сигнал, представляющий собой конечное множество функций у = < у1(t), ... , уm(t} >,
z = z(t) - переменная состояния модели a, также характеризующаяся конечным множеством функций z = < z1(t),... , zn(t) >, знание которых в заданный момент времени позволяет определить значения выходных характеристик модели a;
f и g - функционалы (глобальные уравнения системы), задающие текущие значения выходного сигнала у (t) и внутреннего состояния z(t)

1.4, 1.5
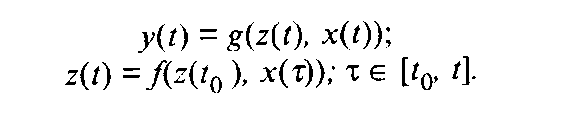
Соотношения (1.4) и (1.5) называют уравнением наблюдения и уравнением состояния системы соответственно. Если в описание системы введены функционалы f и g, то она уже не рассматривается как «черный ящик». Однако для многих систем определение глобальных уравнений оказывается делом трудным и зачастую даже невозможным, что и объясняет необходимость использования этого термина.
Кроме выражения (1.2) систему задают тремя аксиомами.
Аксиома 1. Для системы определены пространство состояний Z, в которых может находиться система, и параметрическое пространство Т, в котором задано поведение системы.
В связи с этим математические описания вида (1.3) принято называть динамическими системами, так как они отражают способность систем изменять состояния z (t() в параметрическом пространстве Т. В отличие от динамических статические системы таким свойством не обладают. В качестве параметрического пространства обычно рассматривается временной интервал (0, ).
Аксиома 2. Пространство состояний Z содержит не менее двух элементов. Эта аксиома отражает естественное представление о том, что сложная система может находиться в разных состояниях.
Аксиома 3. Система обладает свойством функциональной эмерджентности.
Эмерджентность (целостность) - это такое свойство системы 5, которое принципиально не сводится к сумме свойств элементов, составляющих систему, и не выводится из них:
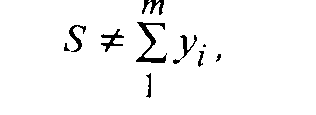
где yi - i-я характеристика системы S;
т - общее количество характеристик.
При таком рассмотрении система является совокупностью моделей и, главное, отражает семантику предметной области в отличие от неинтерпретированных частных математических моделей. Другими словами, система - это совокупность взаимосвязанных элементов, обладающая интегративными свойствами (эмерджентностью), а также способ отображения реальных объектов.
В рамках изучаемой дисциплины под сложной кибернетической системой понимается реальный объект с управлением и его отображение в сознании исследователя как совокупность моделей, адекватная решаемой задаче.
1.2.3. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ СИСТЕМНОГО АНАЛИЗА
Для оперирования основными понятиями системного анализа будем придерживаться следующих словесно-интуитивных или формальных определений.
Элемент - некоторый объект (материальный, энергетический, информационный), обладающий рядом важных свойств и реализующий в системе определенный закон функционирования Fs, внутренняя структура которого не рассматривается.
Формальное описание элемента системы совпадает с описанием подмодели a. Однако функционалы f и g заменяются на закон функционирования Fs, и в зависимости от целей моделирования входной сигнал х(t) может быть разделен на три подмножества:
• неуправляемых входных сигналов хi X, i = 1, ... , kx, преобразуемых рассматриваемым элементом;
• воздействий внешней среды nv N, v = 1, ... , kn, представляющих шум, помехи;
• управляющих сигналов (событий) иm U, т = 1, ... , ku, появление которых приводит к переводу элемента из одного состояния в другое.
Иными словами, элемент - это неделимая наименьшая функциональная часть исследуемой системы, включающая < х, п, и, у, Fs > и представляемая как «черный ящик» (рис. 1.5). Функциональную модель элемента будем представлять как у(t) = Fs (х, n, и,t).
Входные сигналы, воздействия внешней среды и управляющие сигналы являются независимыми переменными. При строгом подходе изменение любой из независимых переменных влечет за собой изменение состояния элемента системы. Поэтому в дальнейшем будем обобщенно обозначать эти сигналы как х(t), а функциональную модель элемента - как у(t) = Fs(x(t)), если это не затрудняет анализ системы.