ВУЗ: Смоленский областной казачий институт промышленных технологий и бизнеса
Категория: Лекция
Дисциплина: Моделирование систем
Добавлен: 19.11.2018
Просмотров: 968
Скачиваний: 5
Классификация видов моделирования систем
Классификация видов моделирования может быть проведена по разным основаниям. Один из вариантов классификации приведен на рисунке.
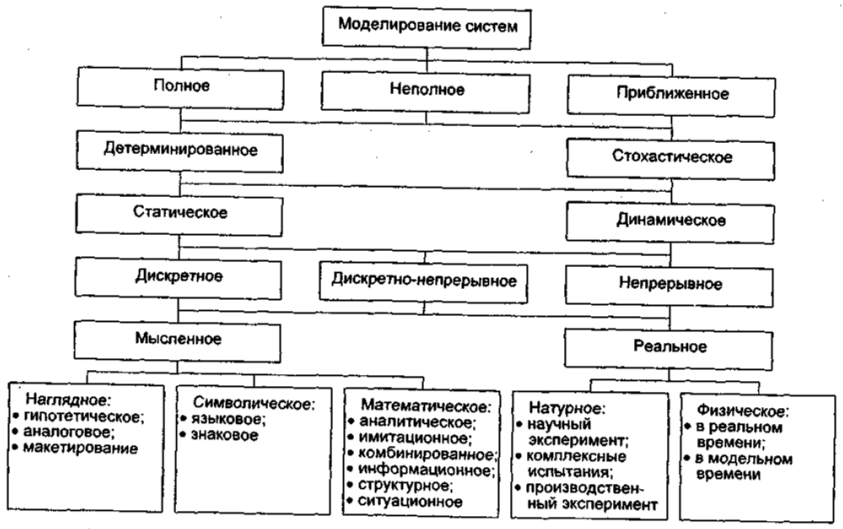
Рис. — Пример классификации видов моделирования
В соответствии с классификационным признаком полноты моделирование делится на: полное, неполное, приближенное.
При полном моделировании модели идентичны объекту во времени и пространстве.
Для неполного моделирования эта идентичность не сохраняется.
В основе приближенного моделирования лежит подобие, при котором некоторые стороны реального объекта не моделируются совсем. Теория подобия утверждает, что абсолютное подобие возможно лишь при замене одного объекта другим точно таким же. Поэтому при моделировании абсолютное подобие не имеет места. Исследователи стремятся к тому, чтобы модель хорошо отображала только исследуемый аспект системы. Например, для оценки помехоустойчивости дискретных каналов передачи информации функциональная и информационная модели системы могут не разрабатываться. Для достижения цели моделирования вполне достаточна событийная модель, описываемая матрицей условных вероятностей переходов i-го символа алфавита в j-й.
В зависимости от типа носителя и сигнатуры модели различаются следующие виды моделирования: детерминированное и стохастическое, статическое и динамическое, дискретное, непрерывное и дискретно-непрерывное.
Детерминированное моделирование отображает процессы, в которых предполагается отсутствие случайных воздействий.
Стохастическое моделирование учитывает вероятностные процессы и события.
Статическое моделирование служит для описания состояния объекта в фиксированный момент времени, а динамическое — для исследования объекта во времени. При этом оперируют аналоговыми (непрерывными), дискретными и смешанными моделями.
В зависимости от формы реализации носителя и сигнатуры моделирование классифицируется на мысленное и реальное.
Мысленное моделирование применяется тогда, когда модели не реализуемы в заданном интервале времени либо отсутствуют условия для их физического создания (например, ситуация микромира). Мысленное моделирование реальных систем реализуется в виде наглядного, символического и математического. Для представления функциональных, информационных и событийных моделей этого вида моделирования разработано значительное количество средств и методов.
При наглядном моделировании на базе представлений человека о реальных объектах создаются наглядные модели, отображающие явления и процессы, протекающие в объекте. Примером таких моделей являются учебные плакаты, рисунки, схемы, диаграммы.
В основу гипотетического моделирования закладывается гипотеза о закономерностях протекания процесса в реальном объекте, которая отражает уровень знаний исследователя об объекте и базируется на причинно-следственных связях между входом и выходом изучаемого объекта. Этот вид моделирования используется, когда знаний об объекте недостаточно для построения формальных моделей. Аналоговое моделирование основывается на применении аналогий различных уровней. Для достаточно простых объектов наивысшим уровнем является полная аналогия. С усложнением системы используются аналогии последующих уровней, когда аналоговая модель отображает несколько (или только одну) сторон функционирования объекта.
Макетирование применяется, когда протекающие в реальном объекте процессы не поддаются физическому моделированию или могут предшествовать проведению других видов моделирования. В основе построения мысленных макетов также лежат аналогии, обычно базирующиеся на причинно-следственных связях между явлениями и процессами в объекте.
Символическое моделирование представляет собой искусственный процесс создания логического объекта, который замещает реальный и выражает его основные свойства с помощью определенной системы знаков и символов.
В основе языкового моделирования лежит некоторый тезаурус, который образуется из набора понятий исследуемой предметной области, причем этот набор должен быть фиксированным. Под тезаурусом понимается словарь, отражающий связи между словами или иными элементами данного языка, предназначенный для поиска слов по их смыслу.
Традиционный тезаурус состоит из двух частей: списка слов и устойчивых словосочетаний, сгруппированных по смысловым (тематическим) рубрикам; алфавитного словаря ключевых слов, задающих классы условной эквивалентности, указателя отношений между ключевыми словами, где для каждого слова указаны соответствующие рубрики. Такое построение позволяет определить семантические (смысловые) отношения иерархического (род/вид) и неиерархического (синонимия, антонимия, ассоциации) типа.
Между тезаурусом и обычным словарем имеются принципиальные различия. Тезаурус — словарь, который очищен от неоднозначности, т.е. в нем каждому слову может соответствовать лишь единственное понятие, хотя в обычном словаре одному слову может соответствовать несколько понятий.
Если ввести условное обозначение отдельных понятий, т.е. знаки, а также определенные операции между этими знаками, то можно реализовать знаковое моделирование и с помощью знаков отображать набор понятий — составлять отдельные цепочки из слов и предложений. Используя операции объединения, пересечения и дополнения теории множеств, можно в отдельных символах дать описание какого-то реального объекта.
Математическое моделирование — это процесс установления соответствия данному реальному объекту некоторого математического объекта, называемого математической моделью. В принципе, для исследования характеристик любой системы математическими методами, включая и машинные, должна быть обязательно проведена формализация этого процесса, т.е. построена математическая модель. Вид математической модели зависит как от природы реального объекта, так и от задач исследования объекта, от требуемой достоверности и точности решения задачи. Любая математическая модель, как и всякая другая, описывает реальный объект с некоторой степенью приближения.
Для представления математических моделей могут использоваться различные формы записи. Основными являются инвариантная, аналитическая, алгоритмическая и схемная (графическая).
Инвариантная форма — запись соотношений модели с помощью традиционного математического языка безотносительно к методу решения уравнений модели. В этом случае модель может быть представлена как совокупность входов, выходов, переменных состояния и глобальных уравнений системы. Аналитическая форма — запись модели в виде результата решения исходных уравнений модели. Обычно модели в аналитической форме представляют собой явные выражения выходных параметров как функций входов и переменных состояния.
Для аналитического моделирования характерно то, что в основном моделируется только функциональный аспект системы. При этом глобальные уравнения системы, описывающие закон (алгоритм) ее функционирования, записываются в виде некоторых аналитических соотношений (алгебраических, интегродифференциальных, конечноразностных и т.д.) или логических условий. Аналитическая модель исследуется несколькими методами:
-
аналитическим, когда стремятся получить в общем виде явные зависимости, связывающие искомые характеристики с начальными условиями, параметрами и переменными состояния системы;
-
численным, когда, не умея решать уравнения в общем виде, стремятся получить числовые результаты при конкретных начальных данных (напомним, что такие модели называются цифровыми);
-
качественным, когда, не имея решения в явном виде, можно найти некоторые свойства решения (например, оценить устойчивость решения).
В настоящее время распространены компьютерные методы исследования характеристик процесса функционирования сложных систем. Для реализации математической модели на ЭВМ необходимо построить соответствующий моделирующий алгоритм.
Алгоритмическая форма — запись соотношений модели и выбранного численного метода решения в форме алгоритма. Среди алгоритмических моделей важный класс составляют имитационные модели, предназначенные для имитации физических или информационных процессов при различных внешних воздействиях. Собственно имитацию названных процессов называют имитационным моделированием.
При имитационном моделировании воспроизводится алгоритм функционирования системы во времени — поведение системы, причем имитируются элементарные явления, составляющие процесс, с сохранением их логической структуры и последовательности протекания, что позволяет по исходным данным получить сведения о состояниях процесса в определенные моменты времени, дающие возможность оценить характеристики системы. Основным преимуществом имитационного моделирования по сравнению с аналитическим является возможность решения более сложных задач. Имитационные модели позволяют достаточно просто учитывать такие факторы, как наличие дискретных и непрерывных элементов, нелинейные характеристики элементов системы, многочисленные случайные воздействия и другие, которые часто создают трудности при аналитических исследованиях. В настоящее время имитационное моделирование — наиболее эффективный метод исследования систем, а часто и единственный практически доступный метод получения информации о поведении системы, особенно на этапе ее проектирования.
В имитационном моделировании различают метод статистических испытаний (Монте-Карло) и метод статистического моделирования.
Метод Монте-Карло — численный метод, который применяется для моделирования случайных величин и функций, вероятностные характеристики которых совпадают с решениями аналитических задач. Состоит в многократном воспроизведении процессов, являющихся реализациями случайных величин и функций, с последующей обработкой информации методами математической статистики.
Если этот прием применяется для машинной имитации в целях исследования характеристик процессов функционирования систем, подверженных случайным воздействиям, то такой метод называется методом статистического моделирования.
Метод имитационного моделирования применяется для оценки вариантов структуры системы, эффективности различных алгоритмов управления системой, влияния изменения различных параметров системы. Имитационное моделирование может быть положено в основу структурного, алгоритмического и параметрического синтеза систем, когда требуется создать систему с заданными характеристиками при определенных ограничениях.
Комбинированное (аналитико-имитационное) моделирование позволяет объединить достоинства аналитического и имитационного моделирования. При построении комбинированных моделей производится предварительная декомпозиция процесса Функционирования объекта на составляющие подпроцессы, и для тех из них, где это возможно, используются аналитические модели, а для остальных подпроцессов строятся имитационные модели. Такой подход дает возможность охватить качественно новые классы систем, которые не могут быть исследованы с использованием аналитического или имитационного моделирования в отдельности.
Информационное (кибернетическое) моделирование связано с исследованием моделей, в которых отсутствует непосредственное подобие физических процессов, происходящих в моделях, реальным процессам. В этом случае стремятся отобразить лишь некоторую функцию, рассматривают реальный объект как «черный ящик», имеющий ряд входов и выходов, и моделируют некоторые связи между выходами и входами. Таким образом, в основе информационных (кибернетических) моделей лежит отражение некоторых информационных процессов управления, что позволяет оценить поведение реального объекта. Для построения модели в этом случае необходимо выделить исследуемую функцию реального объекта, попытаться формализовать эту функцию в виде некоторых операторов связи между входом и выходом и воспроизвести данную функцию на имитационной модели, причем на совершенно другом математическом языке и, естественно, иной физической реализации процесса. Так, например, экспертные системы являются моделями ЛПР.
Структурное моделирование системного анализа базируется на некоторых специфических особенностях структур определенного вида, которые используются как средство исследования систем или служат для разработки на их основе специфических подходов к моделированию с применением других методов формализованного представления систем (теоретико-множественных, лингвистических, кибернетических и т.п.). Развитием структурного моделирования являетсяобъектно-ориентированное моделирование.
Структурное моделирование системного анализа включает:
-
методы сетевого моделирования;
-
сочетание методов структуризации с лингвистическими;
-
структурный подход в направлении формализации построения и исследования структур разного типа (иерархических, матричных, произвольных графов) на основе теоретико-множественных представлений и понятия номинальной шкалы теории измерений.
При этом термин «структура модели» может применяться как функциям, так и к элементам системы. Соответствующие структуры называются функциональными и морфологическими. Объектно-ориентированное моделирование объединяет структуры обоих типов в иерархию классов, включающих как элементы, так и функции.
В структурном моделировании за последнее десятилетие сформировалась новая технология CASE. Аббревиатура CASE имеет двоякое толкование, соответствующее двум направлениям использования CASE-систем. Первое из них — Computer-Aided Software Engineering — переводится как автоматизированное проектирование программного обеспечения. Соответствующие CASE-системы часто называют инструментальными средами быстрой разработки программного обеспечения (RAD — Rapid Application Development). Второе — Computer-Aided System Engineering — подчеркивает направленность на поддержку концептуального моделирования сложных систем, преимущественно слабоструктурированных. Такие CASE-системы часто называют системами BPR (Business Process Reengineering). В целом CASE-технология представляет собой совокупность методологий анализа, проектирования, разработки и сопровождения сложных автоматизированных систем, поддерживаемую комплексом взаимосвязанных средств автоматизации. CASE — это инструментарий для системных аналитиков, разработчиков и программистов, позволяющий автоматизировать процесс проектирования и разработки сложных систем, в том числе и программного обеспечения.
Ситуационное моделирование опирается на модельную теорию мышления, в рамках которой можно описать основные механизмы регулирования процессов принятия решений. В центре модельной теории мышления лежит представление о формировании в структурах мозга информационной модели объекта и внешнего мира. Эта информация воспринимается человеком на базе уже имеющихся у него знаний и опыта. Целесообразное поведение человека строится путем формирования целевой ситуации и мысленного преобразования исходной ситуации в целевую. Основой построения модели является описание объекта в виде совокупности элементов, связанных между собой определенными отношениями, отображающими семантику предметной области. Модель объекта имеет многоуровневую структуру и представляет собой тот информационный контекст, на фоне которого протекают процессы управления. Чем богаче информационная модель объекта и выше возможности манипулирования ею, тем лучше и многообразнее качество принимаемых решений при управлении.