Файл: Базы данных - уч. пособие.pdf

3.4 Технология манипулирования данными в реляционной модели

51

при выполнении декартового произведения у отношений-операндов могут быть
одноименные атрибуты, определенные на одном домене.

В результате такой операции было бы создано отношение с одноименными ат-

рибутами, что противоречит определению схемы отношения как множества атри-
бутов, поскольку множество не должно содержать одинаковых элементов. Однако,
удалив один из одноименных атрибутов, мы рискуем потерять часть информации.
Для того чтобы избежать проблем с однозначным определением имен атрибутов,
используется операция переименования.

В целях корректного выполнения реляционных операций при возникновении

конфликтов в именовании атрибутов к одному из отношений-операндов необхо-
димо сначала применить операцию переименования, а уже после этого выполнять
основную операцию.

Операции объединения, пересечения и разности
Для парных теоретико-множественных операций реляционной алгебры необ-

ходимо выполнение некоторых условий. Так, для операций объединения, пересе-
чения и разности — условия совместимости отношений по объединению. Если до-
пустить в реляционной алгебре возможность теоретико-множественного объедине-
ния двух отношений с разными схемами, т. е. с разноименными атрибутами и доме-
нами, то результатом выполнения этих операций будет не отношение реляционной
модели, а таблица разнотипных и разноименных данных. Таким образом, операция
объединения (пересечения и разности) над отношениями корректно выполняется
в том и только том случае, когда отношения обладают одинаковыми заголовками.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Два отношения будут совместимы по объединению, если в заго-
ловках отношений-операндов содержится один и тот же набор
имен атрибутов, и одноименные атрибуты определены на одном
и том же домене или, если понятие домена не поддерживается,
одноименные атрибуты должны быть одного типа.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Если отношения-операнды совместимы во всем, кроме имен атрибутов, то для

выполнения требования совместимости по объединению до выполнения основных
операций необходимо применить операцию переименования для соответствующих
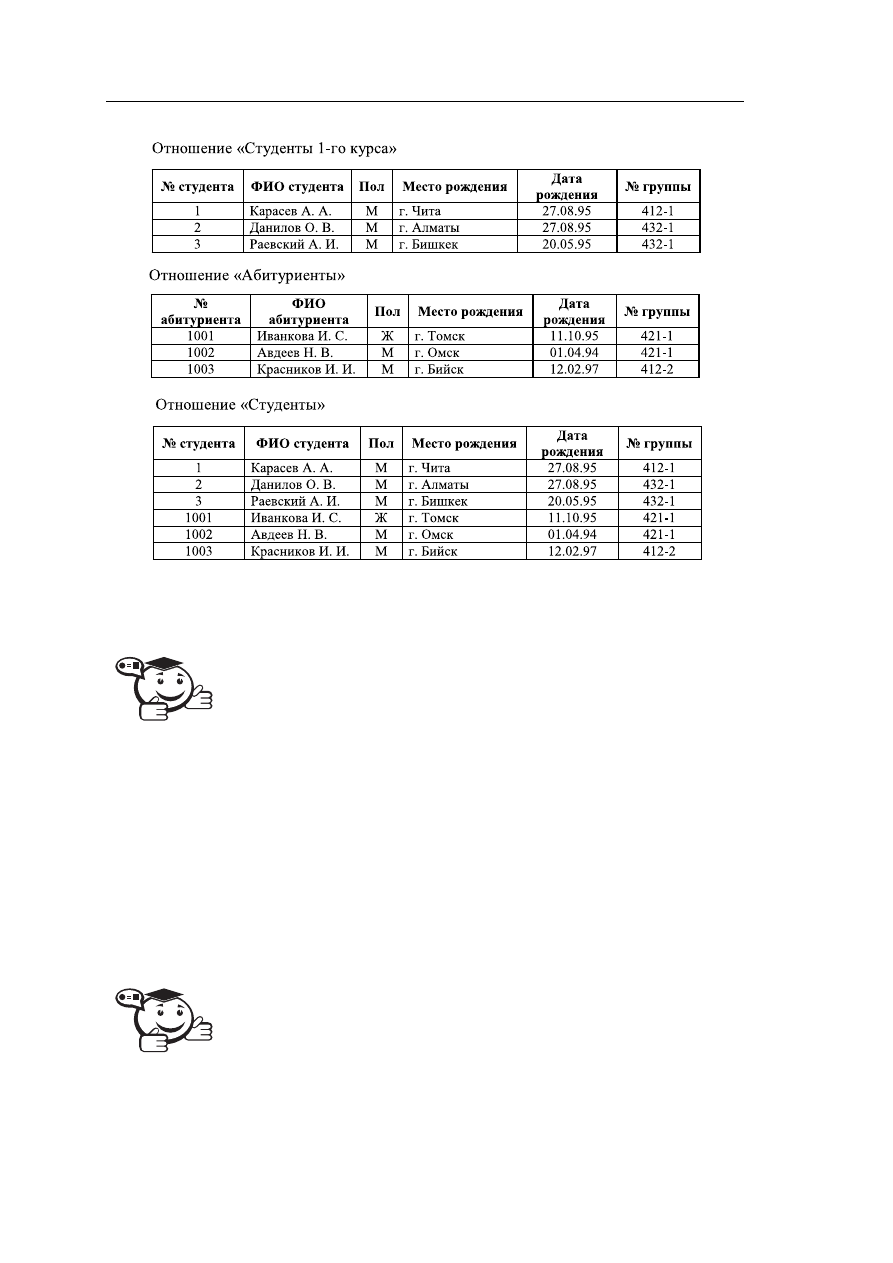
атрибутов. Пример операции объединения представлен на рисунке 3.13.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Если отношения-операнды совместимы по объединению, то при
выполнении над ними операций объединения (пересечения и взятия
разности) результатом является отношение со схемой, совпада-
ющей со схемой каждого из отношений-операндов.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Хотя любая из операций объединения, пересечения и разности может быть

выражена через две другие, эти операции включены Коддом в манипуляционную
часть реляционной модели с целью облегчения построения запросов к БД потен-
циальными пользователями СУБД.

52

Глава 3. Реляционная модель

Рис. 3.13 – Пример выполнения операции объединения

Прямое произведение

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Прямым произведением отношений A и B со схемами, соответ-
ственно (A

1

, A

2

,. . .,A

n

) и (B

1

, B

2

,. . .,B

m

), является отношение C со

схемой (A

1

, A

2

,. . .,A

n

, B

1

, B

2

,. . .,B

m

), которая равна объединению

схем отношений A и B. Кортежи отношения C получены в резуль-
тате конкатенации (присоединения) каждого кортежа из отно-
шения B с каждым кортежем отношения A.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

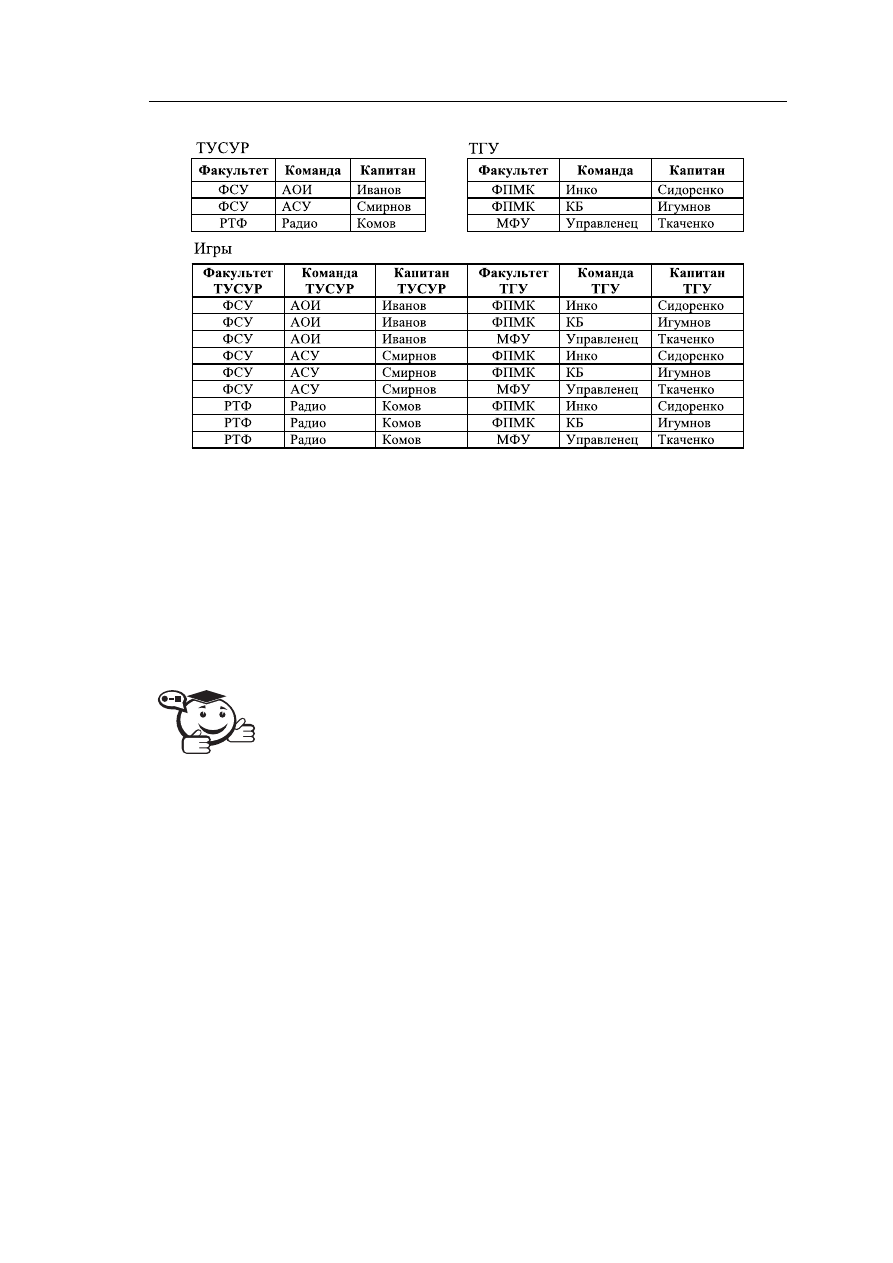
Поясним смысл операции на примере (рис. 3.14). Пусть имеем отношение

«ТУСУР», в котором содержится информация о факультетских командах по баскет-
болу ТУСУРа, и отношение «ТГУ», содержащее аналогичную информацию о ко-
мандах ТГУ. Тогда декартовым произведением отношений «ТУСУР» и «ТГУ» бу-
дет отношение «Игры», содержащее список участников, которые должны играть
попарно.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Два отношения совместимы по взятию прямого произведения
тогда и только тогда, когда все атрибуты этих отношений име-
ют различные имена.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Естественно, что два отношения можно сделать совместимыми по взятию пря-

мого произведения с помощью операции переименования, примененной к одному
из них.

3.4 Технология манипулирования данными в реляционной модели

53

Рис. 3.14 – Пример операции прямого произведения

Отметим, что вышеперечисленные операции являются ассоциативными. Обо-

значим через OP любую из четырех операций, тогда (R

1

OP R

2

) OP R

3

= R

1

(R

2

OP

OP R

3

) и справедлива следующая запись: R

1

OP R

2

OP R

3

, где R

1

, R

2

и R

3

отноше-

ния, удовлетворяющие требованиям выполнения соответствующих операций. Кро-
ме того, все операции, за исключением операции взятия разности, коммутативны,
т. е. R

1

OP R

2

= R

2

OP R

1

.

Операция ограничения

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Для выполнения операции ограничения (выборки) необходимо
наличие двух операндов — ограничиваемого отношения и усло-
вия ограничения. Условие ограничения может иметь либо вид
(a comp-op b), где a и b — имена атрибутов ограничиваемого от-
ношения, для которых осмыслена операция сравнения comp-op;
либо вид (a comp-op const), где a — имя атрибута ограничиваемо-
го отношения, а const — литерально заданная константа [1].
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Операцию ограничения принято также называть операцией выбора.
Результатом операции ограничения является отношение с заголовком, совпадаю-

щим с заголовком отношения-операнда, в тело которого входят кортежи отноше-
ния-операнда, для которых выполняется условие ограничения. Результат опера-
ции ограничения представляется в виде горизонтальной «вырезки» кортежей отно-
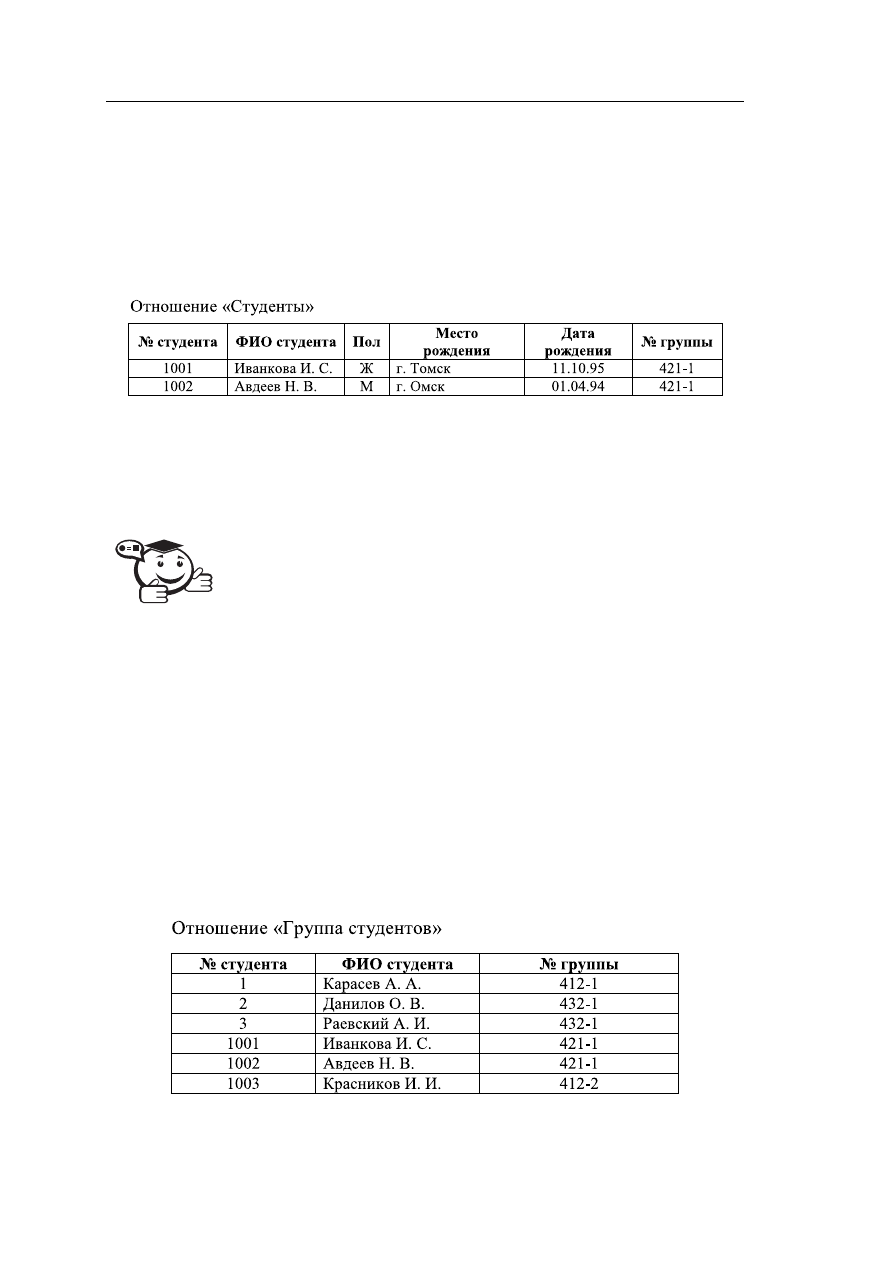
шения-операнда. На рисунке 3.15 приведено отношение «Студенты» (см. рис. 3.13),
к которому применена операция ограничения с условием № группы равен «421-1».

Рассмотрим механизм применения операции ограничения. Пусть UNION обо-

значает операцию объединения, INTERSECT — операцию пересечения, а MINUS —
операцию взятия разности. Для обозначения операции ограничения будем исполь-
зовать конструкцию A WHERE comp, где A — ограничиваемое отношение, а comp —
простое условие сравнения. Пусть comp1 и comp2 — два простых условия ограни-
чения [1], тогда:

54

Глава 3. Реляционная модель

• A WHERE comp1 AND comp2 обозначает то же самое, что и (A WHERE

comp1) INTERSECT (A WHERE comp2);

• A WHERE comp1 OR comp2 обозначает то же самое, что и (A WHERE

comp1) UNION (A WHERE comp2);

• A WHERE NOT comp1 обозначает то же самое, что и A MINUS (A WHERE

comp1).

Рис. 3.15 – Результат выполнения операции ограничения

Итак, допускается использование операций ограничения, где условием ограни-

чения является булевское выражение со стандартными логическими связками типа
AND, OR, NOT и скобками.

Операция взятия проекции

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Для выполнения операции взятия проекции требуется наличие
проецируемого отношения R и списка имен атрибутов, входящих
в схему отношения. Результатом проекции отношения R по спис-
ку атрибутов r

1

, r

2

, . . ., r

n

является отношение с заголовком, опре-

деляемым множеством атрибутов r

1

, r

2

, . . ., r

n

, и телом, состоя-

щим из кортежей вида <r

1

∶ v

1

, r

2

∶ v

2

, . . ., r

n

∶ v

n

> таких, что

в отношении R имеется кортеж, атрибут r

1

которого имеет

значение v

1

, атрибут r

2

имеет значение v

2

,. . ., атрибут r

n

имеет

значение v

n

.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Тем самым при выполнении операции проекции выделяется «вертикальная»

вырезка отношения-операнда [1]. Заметим, что при появлении дублирующих кор-
тежей необходимо исключить таковые из результирующего набора. Так, результа-
том выполнения операции взятия проекции отношения «Студенты» (см. рис. 3.13)
на атрибуты «№ студента», «ФИО студента», «№ группы» является отношение
«Группа студентов» (рис. 3.16).

Рис. 3.16 – Результат операции взятия проекции

3.4 Технология манипулирования данными в реляционной модели

55

Операция соединения отношения

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Результатом выполнения операции соединения отношения R

1

по

атрибуту X с отношением R

2

по атрибуту Y является отноше-

ние R, множество всех кортежей которого является конкатена-
цией таких кортежей a

∈ R

1

и кортежей b

∈ R

2

, для которых

вычисляется условие X * Y , где * есть операция сравнения типа
«

=, ≠, <, >, >=, <=».

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Естественно, что X и Y должны быть определены на одном и том же домене.
Операцию соединения отношений обычно применяют для соединения двух

и более таблиц в одну с целью получения сводных данных о некоторых связанных
сущностях предметной области либо, если одна сущность представлена несколь-
кими отношениями, для восстановления таковой. На рисунке 3.17 приведен при-
мер использования операции соединения отношений R

1

(A

1

, A

2

, A

3

) и R

2

(A

3

, A

4

) по

совпадению значений атрибутов A

3

в обоих отношениях-операндах — т. е. произво-

дится сопоставление преподавателей с их должностями.

Рис. 3.17 – Пример операции соединения

Операция деления отношений
Кроме определения операции деления, приведенного в начале данного раздела,

справедливо следующее определение.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Пусть даны два отношения R

(A

1

, A

2

, . . ., A

n

, B

1

, B

2

, . . ., B

m

) — дели-

мое и S

(B

1

, B

2

, . . ., B

m

) — делитель, где атрибуты B

1

, B

2

, . . ., B

m

об-

щие для обоих отношений, тогда результатом деления отноше-
ний R

/S будет отношение со схемой (A

1

, A

2

, . . ., A

n

) и телом, со-