Файл: Базы данных - уч. пособие.pdf

66

Глава 4. Технология проектирования реляционных баз данных

Первичным ключом отношения «Справочник студентов» является атрибут «№ за-

четной книжки». В отношении имеют место следующие функциональные зависи-
мости:

• «№ зачетной книжки»

→ «ФИО студента»;

• «№ зачетной книжки»

→ «Дата рождения»;

• «№ зачетной книжки»

→ «Место рождения»;

• «№ зачетной книжки»

→ «№ группы».

При проектировании БД третья нормальная форма схем отношений достаточ-

на в большинстве случаев, и приведением к третьей нормальной форме процесс
проектирования реляционной базы данных обычно заканчивается. Однако иногда
полезно продолжить процесс нормализации.

4.1.4 Нормальная форма Бойса—Кодда

Нормальная форма Бойса—Кодда (BCNF) является расширением третьей нор-

мальной формы, вводит дополнительное ограничение по сравнению с 3NF и явля-
ется промежуточным звеном между 3NF и 4NF. Нормальную форму Бойса—Кодда
принято также называть усиленной третьей нормальной формой.

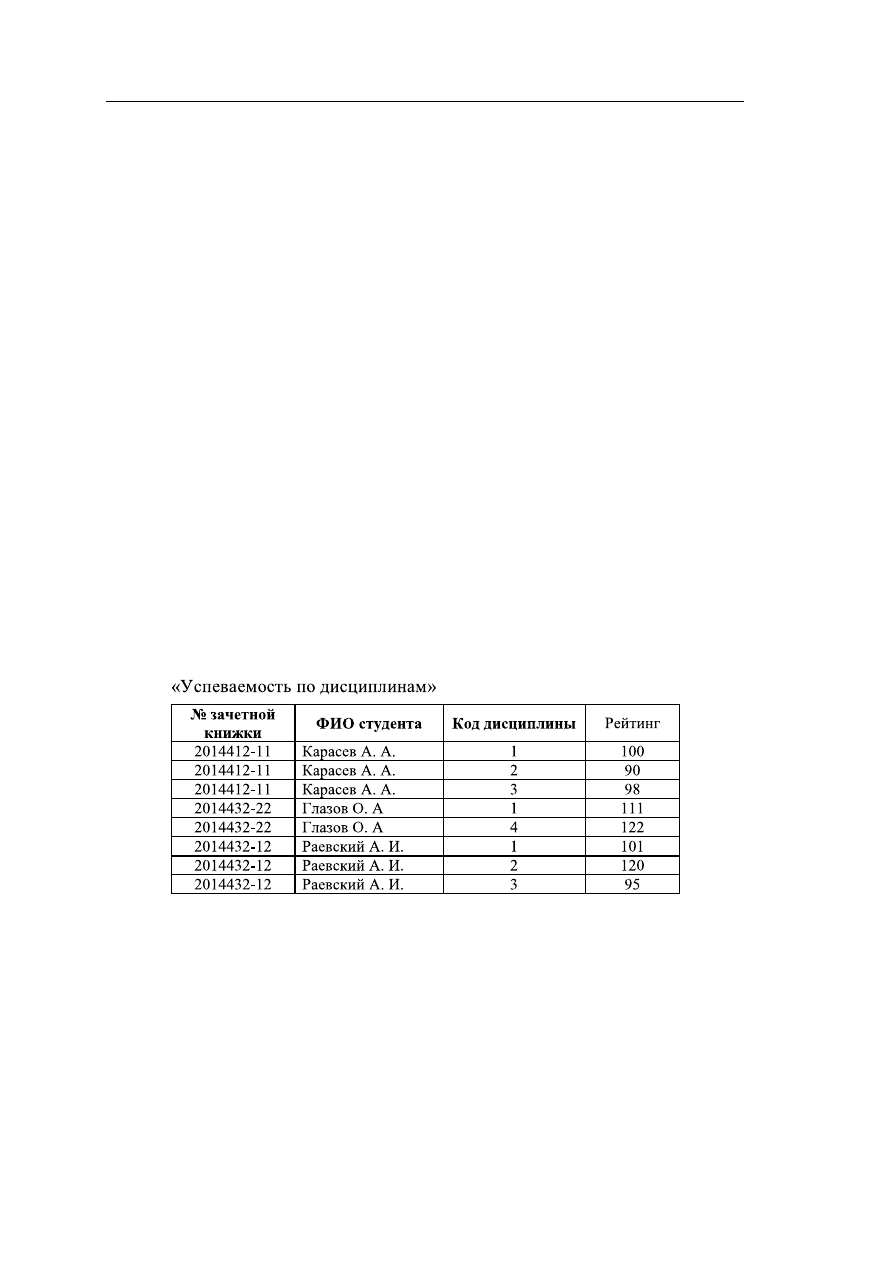
Рассмотрим отношение «Успеваемость по дисциплинам», в котором представ-

лена информация об успеваемости студентов, обучающихся по индивидуальному
плану, т. е. набор предметов для студентов одной группы отличается и зависит от
атрибута «ФИО студента» (рис. 4.5).

Рис. 4.5 – Отношение, не удовлетворяющее BCNF

В данном отношении могут быть определены два первичных ключа, состоящие

из следующих атрибутов:

• PK1: «№ зачетной книжки, Код дисциплины»

• PK2: «ФИО студента, Код дисциплины»

Тогда в отношении будут существовать следующие функциональные зависи-

мости:

• «№ зачетной книжки»

→ «ФИО студента»;

• «№ зачетной книжки»

→ «Код дисциплины»;

4.1 Нормализация отношений

67

• «ФИО студента»

→ «Код студента»;

• «ФИО студента»

→ «Код дисциплины»;

• «№ зачетной книжки», «Код дисциплины»

→ «Рейтинг»;

• «ФИО студента», «Код дисциплины»

→ «Рейтинг».

Ситуация, когда отношение будет находиться в 3NF, но не в BCNF, возника-

ет при условии, что отношение имеет несколько возможных первичных ключей,
состоящих из нескольких атрибутов и имеющих общий атрибут. Для всех прочих
отношений 3NF и BCNF эквивалентны.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Отношение находится в BCNF, если оно находится в 3NF и в нем
отсутствуют зависимости атрибутов, входящих в первичный
ключ, от неключевых атрибутов.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

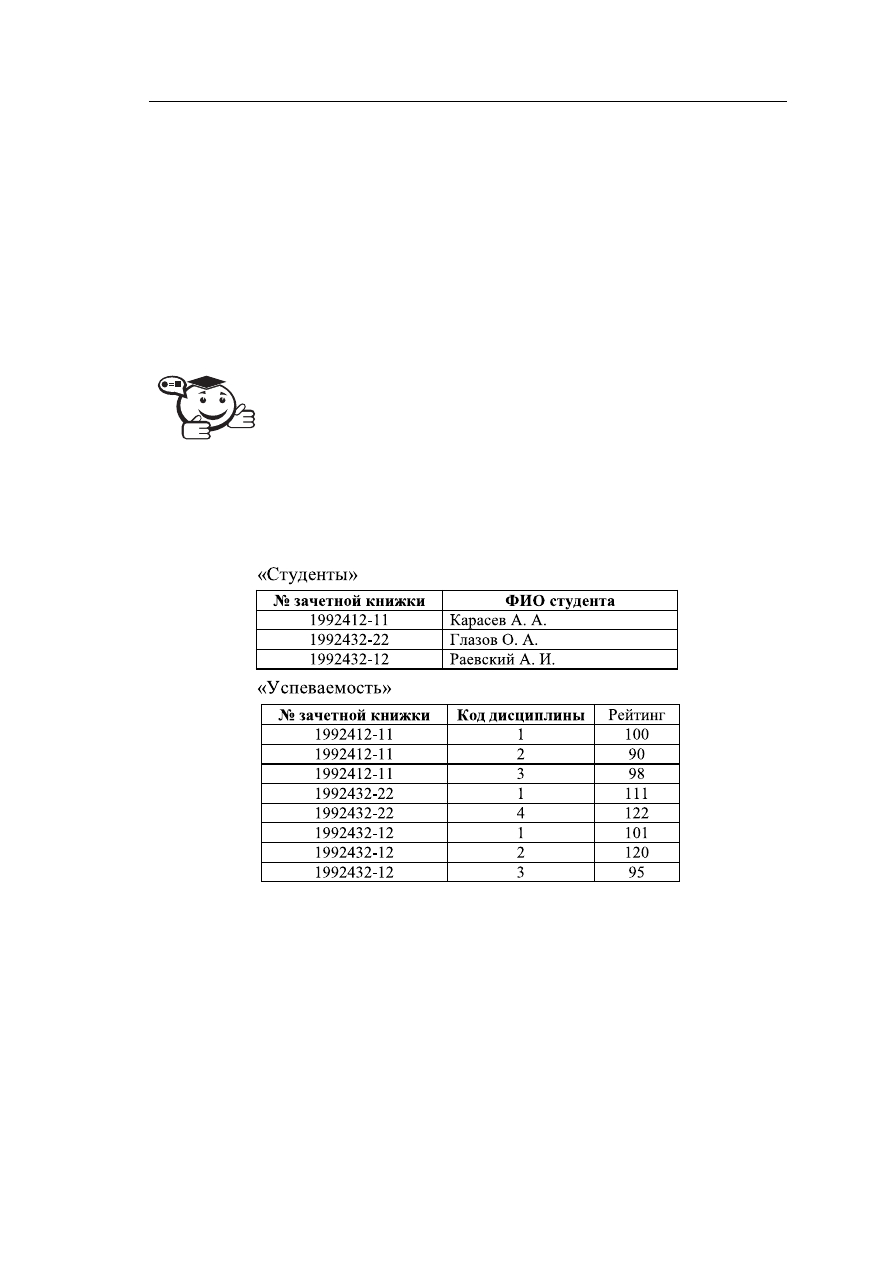
Очевидно, что это требование не выполнено для нашего отношения. Мож-

но произвести его декомпозицию к отношениям «Студенты» и «Успеваемость»
(рис. 4.6).

Рис. 4.6 – Отношения, находящиеся в BCNF

Тогда возможными ключами отношения «Студенты» являются «№ зачетной

книжки» либо «ФИО студента». Функциональные зависимости в этом отношении:

• «№ зачетной книжки»

→ «ФИО студента»;

• «ФИО студента»

→ «№ зачетной книжки».

Возможный ключ отношения «Успеваемость» — «№ зачетной книжки», «Код

дисциплины». Функциональная зависимость:

• «№ зачетной книжки», «Код дисциплины»

→ «Рейтинг».

68

Глава 4. Технология проектирования реляционных баз данных

4.1.5 Четвертая нормальная форма

Четвертая нормальная форма (4NF) касается отношений, для которых харак-

терно наличие повторяющихся наборов данных. В этом случае декомпозиция, ос-
нованная на функциональных зависимостях, не приводит к исключению такой из-
быточности. Здесь необходимо использовать декомпозицию, основанную на мно-
гозначных зависимостях.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

В отношении R

(A, B, C) существует многозначная зависимость

(MVD) A

→→ B в том и только в том случае, если множество зна-

чений B, соответствующее паре значений A и C, зависит только
от A и не зависит от C [1].
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Можно дать еще одно определение многозначной функциональной зависимо-

сти [10]: пусть имеется отношение R, с атрибутами A, B, C; атрибуты B, C много-
значно зависят от A

(A →→ B∣C) тогда и только тогда, когда из того, что в отноше-

нии содержатся кортежи r

1

= (a, b, c

1

) и r

2

= (a, b

1

, c

) следует, что в отношении

содержится также и кортеж r

3

= (a, b, c).

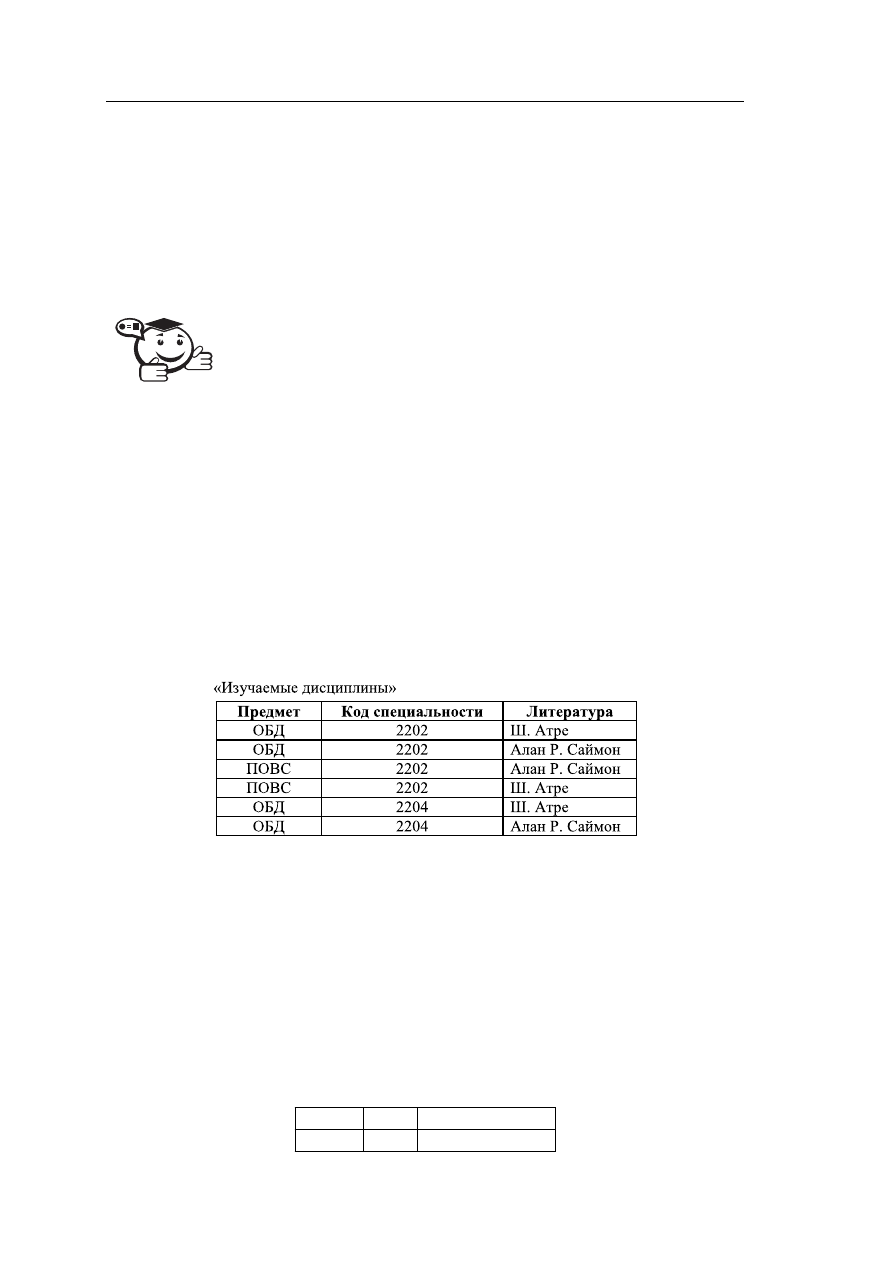
Рассмотрим пример отношения «Изучаемые дисциплины» (рис. 4.7). Отноше-

ние содержит код специальности, для каждой специальности имеется перечень
предметов, а также список литературы, рекомендуемый при изучении соответству-
ющего курса. Студенты специальности могут изучать несколько предметов, и по
разным предметам может быть рекомендована одинаковая литература.

Рис. 4.7 – Отношение, содержащее многозначные зависимости

Каждый кортеж отношения связывает некоторый предмет с конкретной специ-

альностью, на которой изучается данный предмет, и литературой, рекомендован-
ной при изучении данного предмета. Отсюда видно, что единственным ключом,
возможным в нашем отношении, является составной атрибут «Код специальности,
Предмет, Литература».

Следовательно, отношение «Изучаемые дисциплины» находится в BCNF. Но

при этом оно обладает недостатками: если указать, что предмет изучается еще на
одной специальности, то необходимо добавить в отношение весь перечень книг,
рекомендованных для прочтения по данной тематике:

ПОВС

2204

Алан Р. Саймон

ПОВС

2204

Ш. Атре

4.1 Нормализация отношений

69

Так как наше отношение не содержит явных функциональных зависимостей,

то декомпозиция отношения не может быть выполнена на основе функциональ-
ных зависимостей. Однако заметно, что какая-то взаимосвязь между атрибутами
существует. Эта взаимосвязь и есть многозначная зависимость.

В отношении «Изучаемые дисциплины» существуют две многозначные зави-

симости:

• «Предмет»

→→ «Код специальности» — зависимость множества значений

атрибута «Код специальности» от множества значений атрибута «Пред-
мет»;

• «Предмет»

→→ «Литература» — зависимость множества значений атрибута

«Литература» от множества значений атрибута «Предмет».

В общем случае в отношении R

(A, B, C) существует многозначная зависи-

мость A

→→ B в том и только в том случае, когда существует многозначная зави-

симость A

→→ C [1].

Многозначная зависимость A

→→ B∣C называется нетривиальной, если не су-

ществует функциональных зависимостей A

→ B и A → C.

В нашем примере мы имеем дело именно с нетривиальной многозначной за-

висимостью.

Нормализация отношений по 4NF основывается на следующей теореме [1].

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Теорема Фейджина. Отношение R

(A, B, C) можно спроециро-

вать без потерь в отношения R

1

(A, B) и R

2

(A, C) в том и только

в том случае, когда существует многозначная зависимость A

→→

→→ B∣C.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Проецирование без потерь — это такой способ декомпозиции отношения, при

котором исходное отношение полностью и без избыточности восстанавливается
путем естественного соединения полученных отношений [1].

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Отношение R находится в 4NF в том и только в том случае, если
в случае существования многозначной зависимости A

→→ B все

остальные атрибуты R функционально зависят от A [1].

Или иначе, отношение находится в четвертой нормальной фор-
ме тогда и только тогда, когда отношение находится в BCNF
и не содержит нетривиальных многозначных зависимостей.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

В нашем примере можно произвести декомпозицию отношения «Изучаемые

дисциплины» в два отношения «Предметы-специальность» и «Предметы-литера-
тура»:

• «Предметы-Специальность» («Предмет», «Код специальности»);

• «Предметы-Литература» («Предмет», «Литература»).

70

Глава 4. Технология проектирования реляционных баз данных

Оба эти отношения находятся в 4NF и свободны от отмеченных аномалий.

Таким образом, полученные отношения остались полностью ключевыми и в них
по-прежнему нет функциональных зависимостей.

Отношения с нетривиальными многозначными зависимостями возникают, как

правило, в результате естественного соединения двух отношений по общему полю,
которое не является ключевым ни в одном из отношений. Фактически это приводит
к попытке хранить в одном отношении информацию о двух независимых сущно-
стях.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

В качестве еще одного примера можно привести ситуацию, ко-
гда сотрудник может иметь много работ и много детей. Хра-
нение информации о работах и детях в одном отношении приво-
дит к возникновению нетривиальной многозначной зависимости
Работник

→→ Работа|Дети.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

4.1.6 Пятая нормальная форма

В предыдущих примерах процесс нормализации строился путем декомпозиции

одного отношения в два. В отдельных случаях это сделать не удается, тогда при-
ходится проводить декомпозицию в большее число отношений, каждое из которых
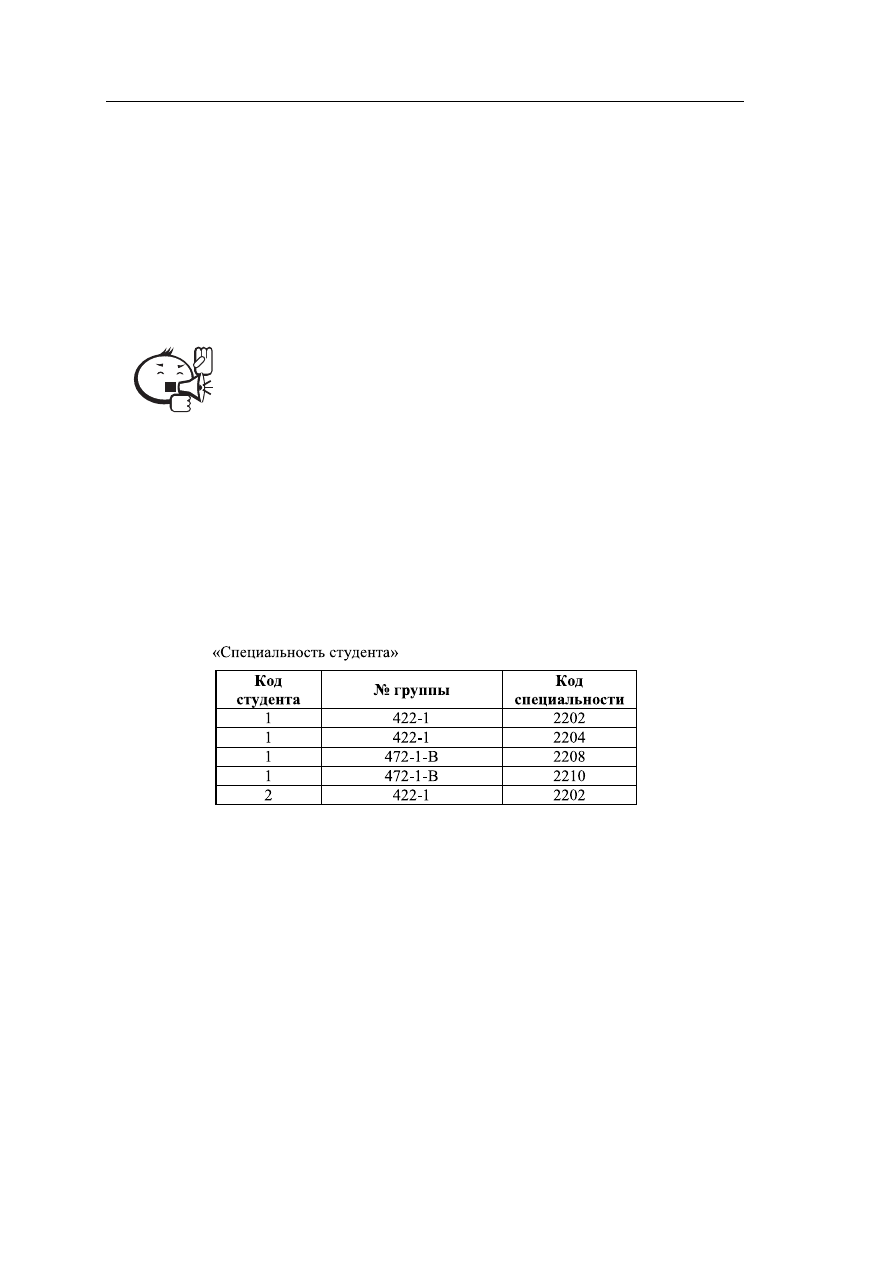
обладает лучшими свойствами. Рассмотрим отношение «Специальность студента»
(рис. 4.8).

Рис. 4.8 – Пример отношения, не находящегося в 5NF

Предположим, что один и тот же студент может обучаться в нескольких груп-

пах и обучаться в каждой группе по нескольким специальностям. Первичным
ключом этого отношения является полная совокупность его атрибутов; отсутству-
ют функциональные и многозначные зависимости. Поэтому отношение находится
в 4NF. Однако в нем могут существовать аномалии, которые нельзя устранить пу-
тем декомпозиции этого отношения в два. Всевозможные проекции отношения,
включающие по два атрибута, представлены на рисунке 4.9.

Из этого примера нетрудно заметить, что отношение R не восстанавливается

ни по одному из попарных соединений R

1

и R

2

, R

2

и R

3

и т. д. Например, в резуль-

тате соединения отношения R

1

и R

2

получим отношение R

4

, которое отличается от

первоначального отношения R (рис. 4.10).

Аналогично можно попытаться произвести другие попарные соединения, и ни

одно из них не восстанавливает отношение R, однако первоначальный вид наше-
го отношения R восстанавливается соединением всех трех проекций. Это говорит