ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 5646
Скачиваний: 10
101
5.2.1 Проблема четырёх красок
Что
можно
сказать
о
хроматическом
числе
графа
,
если
из
-
вестно
,
что
он
плоский
?
Очевидно
,
оно
может
быть
равным
1,2,3.
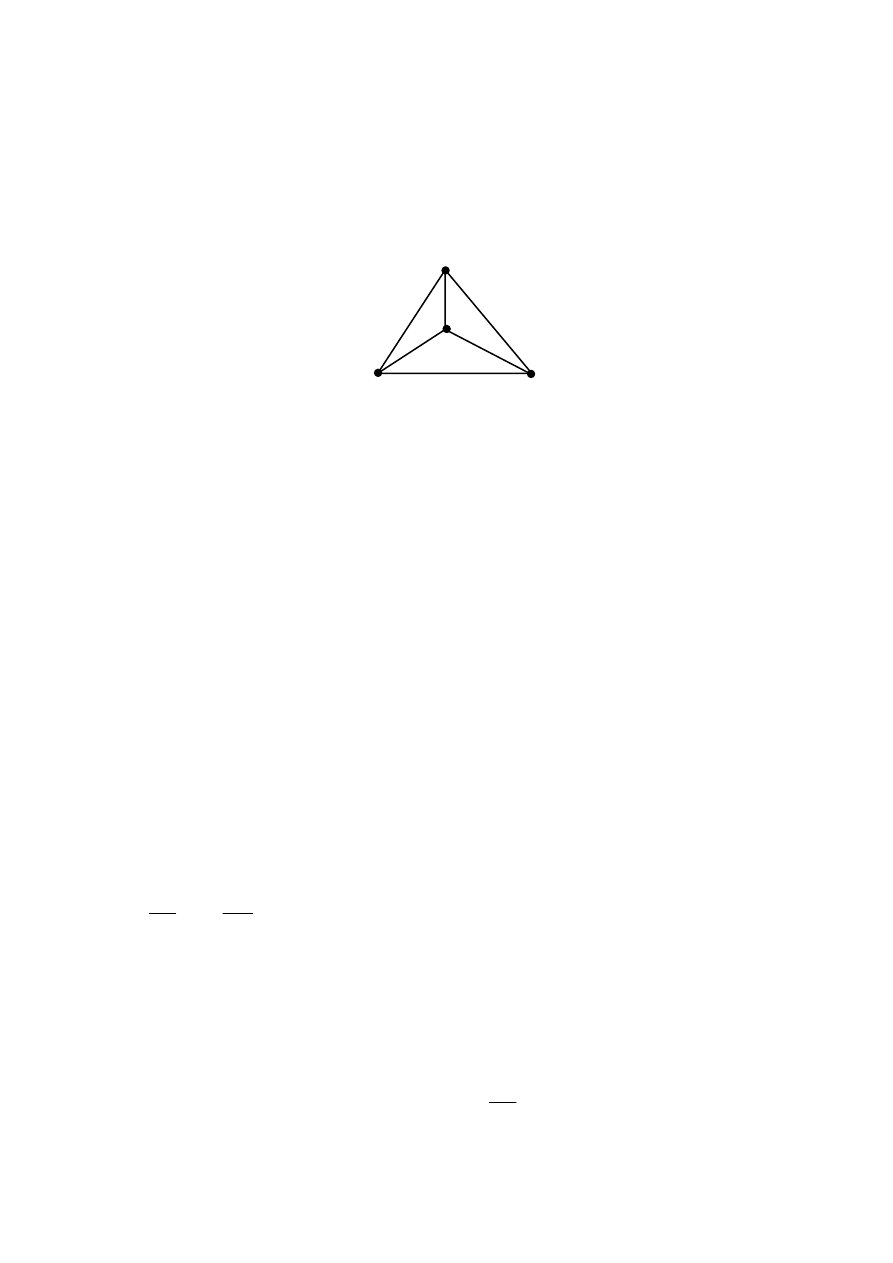
Для
графа
на
рис
. 5.2.4
хроматическое
число
равно
четырём
.
До
сих
пор
не
удавалось
построить
ни
одного
плоского
гра
-
фа
L с
4
)
(
>
L
γ
,
что
даёт
основание
выдвинуть
гипотезу
четырёх
красок
:
хроматическое
число
плоского
графа
никогда
не
превос
-
ходит
4.
Первоначально
эта
гипотеза
в
терминах
раскраски
карт
опубликована
А
.
Кэли
в
1878
году
,
хотя
постановка
этой
пробле
-
мы
осуществлена
ещё
А
.
Мёбиусом
в
1840
году
.
До
настоящего
времени
гипотеза
не
доказана
и
не
опроверг
-
нута
.
Теорема.
Если
L = (X,U,P)
−
плоский
граф
,
то
5
)
(
≤
L
γ
.
В
заключение
заметим
,
что
для
решения
задач
раскраски
возможным
является
использование
аппарата
дискретного
про
-
граммирования
.
Пусть
необходимо
проверить
возможность
раскраски
вер
-
шин
графа
посредством
P
цветов
.
Каждому
варианту
раскраски
ставится
в
соответствие
система
булевых
переменных
y
iq
)
,
1
,
,
1
(
p
q
n
i
=
=
,
где
y
iq
равна
единице
,
если
вершина
x
i
имеет
цвет
q
и
равна
нулю
в
противоположном
случае
.
Положим
также
r
ij
= 1
,
если
x
i
−
концевая
вершина
ребра
U
j
;
r
ij
=
0
в
противном
случае
.
Тогда
задача
сводится
к
определению
значений
для
булевых
переменных
y
iq
,
что
∑
=
=
p
q
iq
y
1
1,
n
i
,
1
=
; (5.2.1)
Рис. 5.2.4

102
∑
=
≥
n
i
iq
ij
y
r
1
1,
m
j
,
1
=
;
p
q
,
1
=
. (5.2.2)
Пусть
необходимо
получить
окраску
вершин
минимальным
количеством
цветов
.
С
этой
целью
каждому
цвету
n
q
,
1
=
отнесём
«
вес
»
−
натуральное
число
a
q
,
таким
образом
,
что
выполняется
неравенство
:
a
1
+a
2
+...+a
q–1
+(n–q+1)a
q
<(n–q)a
1
+a
2
+...+a
q–1
+a
q
+a
q+1
,
n
q
,
1
=
т
.
е
a
q+1
>(n–q)a
q
–(n–q–1)a
1
. (5.2.3)
Это
неравенство
гарантирует
,
что
«
самая
лёгкая
»
окраска
вершин
графа
с
помощью
q+1
цветов
всё
-
таки
«
тяжелее
»,
чем
«
самая
тяжёлая
»
окраска
q
цветами
.
Неравенство
(5.2.3)
наверняка
выполняется
,
если
a
q+1
=(n–q)a
q
–(n–q–1)a
1
+1,
полагая
a
1
=1,
мы
получим
a
q+1
=(n–q)[a
q
–1]+2,
откуда
находим
последовательно
(
независимо
от
графа
L):
a
2
=2, a
3
=n, a
n
=n
2
–4n+5,...
Тогда
задача
раскраски
вершин
графа
сводится
к
определе
-
нию
самой
лёгкой
раскраски
:
найти
минимум
∑∑
= =
⋅
n
i
q
q
iq
q
y
a
1
1
при
ограничениях
(5.2.1, 5.2.2).
По
найденным
y
iq
хроматическое
число
вычисляется
как
( )
(
)
∑
∏
=
=
⎥
⎦
⎤
⎢
⎣
⎡
−
−
=
p
q
n
i
iq
L
y
1
1
1
1
γ
.