ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 5524
Скачиваний: 27

26
Перенося тезис Черча на алгоритмы, сопутствующие рекурсив-
ным функциям, можно сформулировать следующую гипотезу: каков
бы ни был алгоритм, перерабатывающий набор целых неотрица-
тельных чисел в целые неотрицательные числа, существует эквива-
лентный ему алгоритм, сопутствующий рекурсивной функции.
Опираясь на эту гипотезу, можно сделать вывод о том, что вы-
полнение алгоритма в определенном смысле эквивалентно вычисле-
нию значения рекурсивной функции, а невозможность рекурсивной
функции означает и невозможность алгоритма.
Подчеркнем еще раз, что как тезис Черча, так и следующие из
него гипотезы не имеют доказательства и принципиально не могут
быть доказаны, поскольку в них речь идет об алгоритмах в интуи-
тивном смысле, не являющихся математическими объектами.
2.3
Машины
Тьюринга
Из интуитивного понятия алгоритма следует, что вычисления в
соответствии с некоторым алгоритмом выполняются механически и
их можно поручить машине. Процесс, происходящий в такой маши-
не, должен обладать всеми свойствами алгоритмического процесса:
дискретностью, результативностью, детерминированностью. Анг-
лийский математик А. Тьюринг (1912-1954 г.г.) в 1936 г. выполнил,
а в 1937 г. опубликовал работу, в которой уточнил понятие алгорит-
ма, прибегая к воображаемой вычислительной машине, известной
теперь под названием машины Тьюринга. Аналогичную концеп-
цию машины позднее и независимо от Тьюринга ввел американский
математик Э. Пост (1897-1954), поэтому упомянутую машину ино-
гда называют машиной Тьюринга-Поста. Идея Тьюринга возникла
еще до появления ЭВМ и потому, по-видимому, не зависит от них.
Итак, машина Тьюринга – это математическое понятие, введенное
как формальное уточнение интуитивного понятия алгоритма.
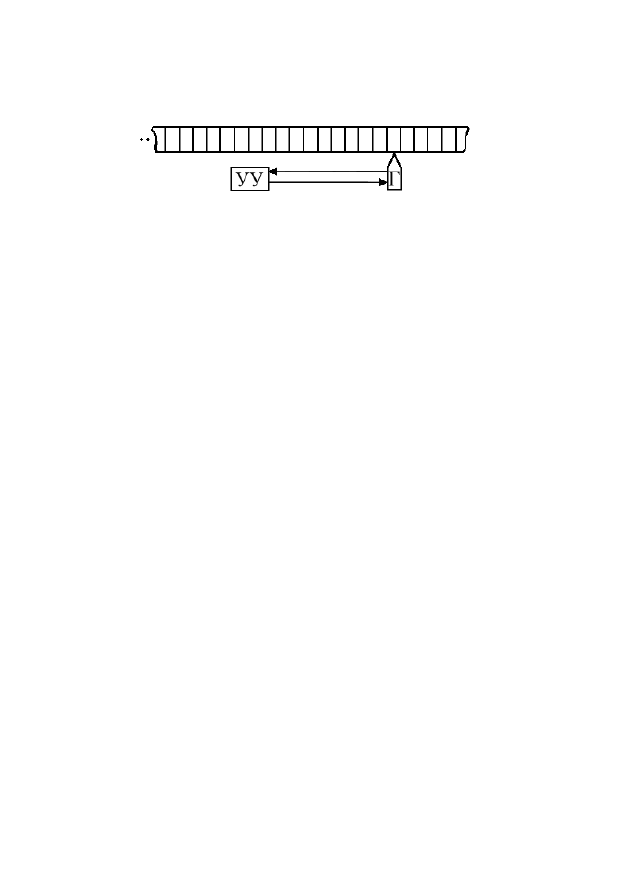
В каждой машине Тьюринга (рис 2.2) присутствуют три части:
1) внешняя память; 2) считывающая и записывающая головка;
3) управляющее устройство.
27
Внешняя память представляет собой неограниченную в обе
стороны ленту, разделенную на ячейки одинаковой длины. Известны
варианты машины Тьюринга с неограниченной лентой в правом на-
правлении, а также с конечной лентой. В последнем случае предпо-
лагается, что справа могут пристраиваться новые ячейки, так что
здесь лента тоже может считаться потенциально неограниченной в
правом направлении. В каждой ячейке может быть один из симво-
лов a
1
, ..., a
m
. Ячейка, не содержащая ни одного из этих символов,
называется пустой. Для обозначения пустой ячейки используют спе-
циальный символ a
0
(или 0). Если в ячейке записан символ a
i
, то го-
ворят, что ячейка находится в состоянии a
i
. Множество символов
A = {a
0
, a
1
,..., a
m
} называется внешним алфавитом машины.
Считывающая и записывающая головка – устройство, ко-
торое в каждый определенный момент времени располагается на-
против некоторой ячейки ленты, которая называется обозреваемой
или воспринимаемой ячейкой. По командам из управляющего уст-
ройства головка может стереть символ, записанный в обозреваемой
ячейке, и записать новый, а также передвинуться вправо или влево
вдоль ленты на одну ячейку.
Управляющее устройство вырабатывает команды, посту-
пающие на головку. В свою очередь с головки на вход управляюще-
го устройства поступает символ обозреваемой ячейки. Управляющее
устройство может находиться в одном из конечного числа состоя-
ний, совокупность которых обозначается через Q = {q
0
, q
1
, ..., q
n
} и
образует внутренний алфавит машины (или алфавит внутренних
состояний), а состояние управляющего устройства называется со-
стоянием внутренней памяти. Одно из внутренних состояний на-
зывается заключительным (обычно это q
0
). В это состояние внут-
ренняя память приходит по окончании работы машины; символ,
обозначающий заключительное состояние, называется стоп-
символом. Управляющее устройство работает в дискретном време-
Рис. 2.2 – Состав машины Тьюринга

28
ни, при этом команды, вырабатываемые им в i-м такте работы, оп-
ределяются символом обозреваемой ячейки и состоянием внутрен-
ней памяти. В результате выполнения команд к началу (i+1)-го такта
работы может быть изменен символ обозреваемой ячейки, записы-
вающая головка может быть передвинута вправо или влево, а также
может быть изменено состояние внутренней памяти. Состоянием
машины Тьюринга, или ее конфигурацией, называется совокуп-
ность, образованная последовательностью символов состояний яче-
ек ленты a
i1
, a
i2
, ..., a
ir
, символом внутреннего состояния q
j
и номе-
ром k воспринимаемой ячейки. Эти данные записываются в виде
машинного слова
a
i1
, a
i2
, ..., a
ik-1
, q
j
, a
ik
, ..., a
ir
.
Каждое машинное слово содержит лишь одно вхождение сим-
вола q
j
(он записывается слева от обозреваемой ячейки). Работу ма-
шины Тьюринга можно представить как последовательное преобра-
зование машинных слов в соответствии с некоторой программой.
Цель работы машины Тьюринга – преобразование слова, записан-
ного на ленте. Чтобы «запустить» машину Тьюринга, надо помес-
тить ее головку напротив нужной ячейки и привести внутреннюю
память машины Тьюринга в исходное состояние.
Работа машины Тьюринга состоит из тактов. В каждом из них
выполняется преобразование конфигурации, в которой машина
Тьюринга находится в данный момент времени i (i = 1, 2, ...), в кон-
фигурацию, в которой машина Тьюринга будет находиться в момент
i+1. Это преобразование включает в себя:
1)
изменение состояния q
j
в некоторое состояние q
l
;
2)
замену буквы a
ik
, записанной в обозреваемой ячейке, неко-
торой буквой a
pk
;
3)
сдвиг головки на одну ячейку влево или вправо (головка
может и не сдвинуться).
Такое преобразование называется командой машины Тьюрин-
га. Символически команда записывается в виде
q
i
a
ik
→
q
l
a
pk
R,
где R – одна из букв Л, П, С (влево, вправо, сохранение положения
головки).
Совокупность всех команд, которые выполняет машина Тью-
ринга, называется ее программой.

29
Для каждой буквы a
i
∈ A и состояния q
j
∈ Q программа содер-
жит в точности одну команду с левой частью q
j
a
i
. Поэтому работа
машины Тьюринга определится однозначно, если фиксировать кон-
фигурацию K
1
, с которой она начинает работать. А именно: в пер-
вом такте K
1
преобразуется в K
2
выполнением единственной, при-
менимой к K
1
команды; во втором такте K
2
преобразуется таким же
образом в K
3
и т.д. Работа машины Тьюринга продолжается неогра-
ниченно, с какой бы конфигурации она не начиналась, однако мож-
но ввести некоторые правила остановки этого процесса. Например,
можно использовать понятие заключительных состояний, придя в
которые, машина Тьюринга останавливается. Конфигурация, в кото-
рой машина Тьюринга останавливается, называется заключитель-
ной конфигурацией. Или, например, можно считать, что работа
машины Тьюринга прекращается на некотором такте, если в этом
такте (а, следовательно, и во всех дальнейших) изменения конфигу-
рации не происходит.
В дальнейшем ограничимся рассмотрением машин Тьюринга с
внешним алфавитом A = {0, 1}. Здесь 0 используется для обозначе-
ния пустых ячеек. Произвольное натуральное число x записывается
на ленте в виде последовательности x+1 единиц: 11...1 = 1
x+1
.
При такой записи число 0 обозначается одной единицей, а пус-
тые ячейки используются для разделения чисел на ленте. Так как
любой алгоритм может быть сведен к алгоритму вычисления цело-
численной функции, то двоичный внешний алфавит позволяет по-
строить машину Тьюринга, реализующую любой алгоритм.
Пример 1. Машина, увеличивающая данное число на единицу
– машина «1». Фактически она вычисляет известную из п.2.2.1
функцию следования. В начале работы машины головка восприни-
мает заполненную ячейку (ячейку, содержащую символ 1), и внут-
ренняя память машины находится в состоянии q
1
. В процессе рабо-
ты машина находит справа пустую ячейку, печатает в ней единицу и
останавливается. Условимся, что стрелка Î обозначает преобразо-
вание, осуществляемое машиной в результате выполнения програм-
мы. В данном случае имеем
01
x
q
1
1
y
0 0 Î 01
x+y
q
0
10.
Запишем совокупность команд, составляющих это программу:
q
1
1
→ q
1
1П – после выполнения раз этой команды машина
придет в состояние 01
x+y
q
1
0 0;

30
q
1
0
→ q
0
1С – после выполнения этой команды машина прихо-
дит в состояние 01
x+y
q
0
10.
Пример работы машины при x=3, y=2 приведен в табл. 2.1.
Состояние машины представлено в таблице словом, записан-
ным на ленте с символом внутренней памяти, расположенным под
воспринимаемой ячейкой.
Таблица 2.1 – Пример работы машины «1»
Номер такта
Состояние машины
0
0 1 1 1 1
q
1
1 0 0
1
0 1 1 1 1 1
q
1
0 0
2
0 1 1 1 1 1 0
q
1
0
3
0 1 1 1 1 1 1
q
0
0
Программу машины Тьюринга можно представить в виде табл.
2.2, содержащей необходимые команды.
Таблица 2.2 – Программа машины «1»
q a
0
1
q
1
q
0
1С
q
1
1П
В этой таблице a – символ обозреваемой ячейки; q – символ со-
стояния внутренней памяти.
Пример 2. Машина, «сдвигающая» головку вправо, на сле-
дующий массив единиц – машина «C
+
». Необходимо осуществить
преобразование
01
x
q
1
1
y
0
z
1
w
0 Î 01
x+y
0
z
1
w-1
q
0
10.
Здесь 0
z
означает последовательность из z нулей. Машина на-
ходит следующий справа массив единиц и останавливается, воспри-
нимая самую правую заполненную ячейку.
Программа содержит команды:
q
1
1
→ q
1
1П (через y тактов команда дает слово 01
x+y
q
1
0
z
1
w
0),
q
1
0
→ q
2
0П,