ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 5522
Скачиваний: 27

31
q
2
0
→ q
2
0П (выполнение этих команд приводит к слову
01
x+y
0
z
q
2
1
w
0),
q
2
1
→ q
3
1П,
q
3
1
→ q
3
1П (получается слово 01
x+y
0
z
1
w
q
3
0),
q
3
0
→ q
0
0Л (получается заключительное слово).
Эта программа приведена в табл. 2.3.
Таблица 2.3 – Программа машины «C
+
»
q a
0
1
q
1
q
2
0П
q
1
1П
q
2
q
2
0П
q
3
1П
q
3
q
0
0Л
q
3
1П
Композиция машин Тьюринга
Это понятие играет важную роль при синтезе машин Тьюринга,
осуществляющих требуемые преобразования машинных слов.
Пусть заданы машины Тьюринга P и Q с общим внешним ал-
фавитом {a
0
, a
1
, …, a
m
} и внутренними алфавитами {q
0
, q
1
, …, q
n
} и
{q
0
, q
1
, …, q
k
}. Пусть машина Тьюринга P осуществляет преобразо-
вание машинного слова A в B, а машина Q – преобразование слова
B в слово C. Требуется построить машину Тьюринга R, которая пре-
образовывала бы слово A в слово C. Такое преобразование будет
осуществляться, если R сначала выполнит преобразование по про-
грамме машины Тьюринга P, а затем – машины Q. Очевидно, что
программу машины R можно получить, объединив программы ма-
шин P и Q, причем в программе машины P стоп-символ q
0
заменить
на символ q
n+1
, а в программе машины Q символы q
i
(i = 1,…, k) –
символами q
i+n
, оставив неизменным символ q
0
. Тогда внутренняя
память машины R после выполнения преобразований по программе
машины P приходит в состояние q
n+1
, после чего машина R начинает
работу по программе машины Q. Машина R с внешним алфавитом
{a
0
, a
1
, …, a
m
}, внутренним алфавитом {q
0
, q
1
, …, q
n+k
} и програм-
мой, полученной из программ P и Q указанным способом, называет-
ся композицией машин P и Q, или произведением машины P на
машину Q (обозначается: R = PQ).
Заметим, что программа машины R может быть получена под-
бором нужных команд. При этом найденная программа может ока-

32
заться короче программы, полученной в результате композиции ма-
шин. Однако понятие композиции дает общий метод синтеза машин,
который облегчает построение сложных программ. Существенно то,
что ряд машин Тьюринга, последовательно выполняющих свои про-
граммы, всегда можно заменить одной машиной, являющейся их
композицией.
Произведение машин Тьюринга – некоммутативная операция,
т.е. в общем случае PQ
≠ QP. Произведение одинаковых машин
Тьюринга называется возведением в степень и обозначается как P
n
.
Пример 3. Используя понятие композиции машин Тьюринга,
построим программу машины Т, сдвигающей головку вправо на
следующий массив единиц, изображающий некоторое число w, уве-
личивающей это число на единицу и останавливающейся:
01
x
q
1
1
y
0
z
1
w+1
0 Î 01
x+y
0
z
1
w+1
q
0
10.
Данная машина может быть представлена композицией маши-
ны «C
+
» (пример 2) и машины «1» (пример 1). Для получения табли-
цы команд машины T заменим символ q
0
в табл. 2.3 и символ q
1
в
табл.2.2 символом q
4
. Полученная программа машины T представ-
лена в табл. 2.4.
Непосредственный подбор команд может привести к более ко-
роткой программе машины T (табл. 2.5).
Таблица 2.4 – Программа машины «C
+
1»
q a
0
1
q
1
q
2
0П
q
1
1П
q
2
q
2
0П
q
3
1П
q
3
q
4
0Л
q
3
1П
q
4
q
0
1С
q
4
1П
Таблица 2.5 – Более короткая программа машины Т
q a
0
1
q
1
q
2
0П
q
1
1П
q
2
q
2
0П
q
3
1П
q
3
q
0
1С
q
3
1П
33
Итерация машин Тьюринга
Кроме операции композиции при синтезе программ машин
Тьюринга используется операция итерации. Рассмотрим машину T
1
,
имеющую k заключительных состояний внутренней памяти q
01
, …,
q
0k
. Отождествим одно из этих состояний, (например, q
0i
) с началь-
ным состоянием машины. Операция отождествления одного из за-
ключительных состояний внутренней памяти машины с ее исход-
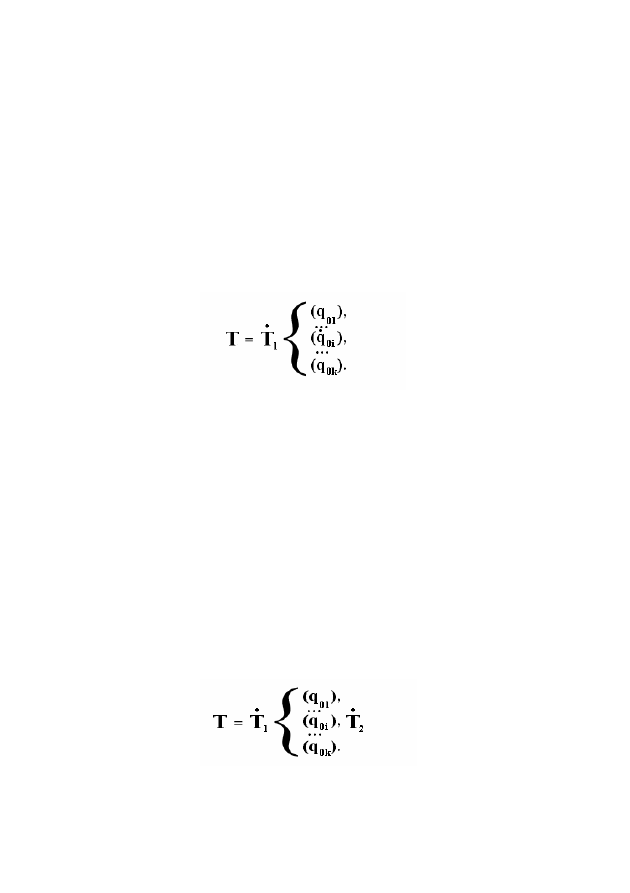
ным состоянием называется операцией итерации. Машину T, по-
лученную в результате итерации машины T
1
, обозначим следующим
образом:
Точки над символами указывают на отождествление i–го за-
ключительного состояния с начальным состоянием машины T
1
. В
результате итерации получим машину, внутренняя память которой
во время работы совершает один или несколько замкнутых циклов.
Если при выполнении программы внутренняя память машины
должна прийти в состояние q
0i
, то она возвращается в начальное
состояние и машина вновь начинает работу. Это продолжается до
тех пор, пока ее внутренняя память не придет в какое-либо из ос-
тальных заключительных состояний. Если машина T
1
имеет одно
заключительное состояние, то в результате итерации получаем ма-
шину, не имеющую заключительных состояний. Такая машина ра-
ботает по замкнутому циклу бесконечно или останавливается, если в
процессе работы получено машинное слово, к которому программа
неприменима.
Итерация может объединиться с композицией машин. Напри-
мер, в машине
после того, как внутренняя память приходит в состояние q
0i
, выпол-

34
няется программа T
2
, после чего внутренняя память приходит в на-
чальное состояние и вновь выполняется программа T
1
.
Использование операций композиции и итерации позволяет по-
строить из простых машин более сложные. При этом сложные ма-
шины удается описать компактным выражением.
Теорема Тьюринга
Рассмотрим вычисление с помощью машин Тьюринга значений
какой-либо функции
ƒ (x
1
, …, x
n
). Определим стандартную форму
записи исходных данных и полученного результата и стандартное
положение головки в начале и в конце вычисления. Число x записы-
вается совокупностью x + 1 единиц. Считаем, что два числа распо-
ложены рядом (подряд), если между записями чисел имеется одна
пустая ячейка. Для простоты условимся, что внешняя память пред-
ставляет собой ленту, неограниченную в правом направлении. Оста-
вим пустой самую левую ячейку ленты и запишем далее подряд чис-
ла x
1
, …, x
n
. Будем говорить, что головка воспринимает систему чи-
сел < x
1
, …, x
n
> в стандартном положении, если эти числа записаны
подряд и головка воспринимает самую правую заполненную ячейку
в представлении последнего из чисел x
n
.
Пусть в начале работы машина воспринимает в стандартном
положении систему чисел < x
1
, …,x
n
>. Будем говорить, что машина
вычисляет частичную функцию
ƒ (x
1
, …,x
n
), если:
- для всех систем чисел < x
1
, …,x
n
>, для которых функция
ƒ (x
1
, …, x
n
) определена, по окончании работы машина воспринима-
ет в стандартном положении систему чисел < x
1
, …, x
n
,
ƒ (x
1
, …,x
n
)>
и внутренняя память находится в заключительном состоянии, т.е.
01
x1+1
… 0 1
xn+1
q
1
10 Î 01
x1+1
…0 1
xn+1
0 1
ƒ(x1, …,xn)
q
0
1 0
- для всех систем чисел < x
1
, …, x
n
>, для которых функция не
определена, машина, начав работать, не приходит в заключительное
состояние.
Функция называется вычислимой на машине Тьюринга, если
существует машина Тьюринга, вычисляющая эту функцию.
Теорема. Класс функций, вычислимых на машинах Тьюринга,
совпадает с классом частично рекурсивных функций.
Эта теорема доказывает эквивалентность уточнений понятия
алгоритма с помощью машин Тьюринга и с помощью теории рекур-
сивных функций.

35
2.4
Нормальные
алгорифмы
Маркова
Советский математик А.А. Марков в 1947 г. разработал другой
путь уточнения алгоритма. Заметим, что термины «алгоритм» и «ал-
горифм» в то время существовали равноправно, и лишь гораздо
позднее термин «алгоритм» получил более широкое распростране-
ние. А.А. Марковым разработана строгая теория класса алгоритмов,
которые он назвал нормальными алгорифмами. Наряду с рекур-
сивными функциями и машинами Тьюринга нормальные алгорифмы
получили известность в качестве одного из наиболее удобных уточ-
нений общего интуитивного представления об алгоритме.
Как и машины Тьюринга, нормальные алгоритмы в качестве
исходных данных и искомых результатов имеют строки символов
(букв) – слова. Предположим, что, как и в случае машин Тьюринга,
заранее определен некоторый алфавит. Обозначим его через A. Бук-
ву, одинаковую с одной из букв, входящих в алфавит A, называют
буквой в A. Слово, состоящее из букв в A, называют словом в A.
Для удобства рассуждений допускаются и пустые слова, которые не
имеют в своем составе ни одной буквы.
Если A и B – два алфавита, причем каждая буква алфавита A
является буквой в B, а хотя бы одна из букв алфавита B не является
буквой в A, то B называется расширением A.
Например, если
A = {а, б, в, г, д}, B = {1, а, б, в, г, д, е},
то B является расширением A, поскольку содержит две буквы («1» и
«е»), не являющиеся буквами в A, тогда как все буквы алфавита A
являются буквами в B.
Рассмотрим какое-либо конкретное слово для определенности в
алфавите русских букв, например слово «система». Из него можно
вырезать «подслова», например «сис», «ист», «тема» и т.п., наконец
однобуквенное слово, например «а». Про такие «подслова» говорят,
что они входят в рассматриваемое слово или являются вхождения-
ми в него. Отметим, что в наше слово «система» входит и пустое
слово, причем несколько раз. Оно входит перед первой буквой, ме-
жду каждыми двумя буквами и, наконец, после последней буквы,
т.е., в нашем случае, 8 раз.
Условимся обозначать слова заглавными латинскими буквами,
при этом они не должны быть буквами в применяемом алфавите.