ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 7075
Скачиваний: 35
4.5 Минимизация булевых функций
81
5. Все единицы (нули) в карте (даже одиночные) должны быть охвачены кон-
турами. Любая единица (нуль) может входить в контуры произвольное ко-
личество раз.
6. Множество контуров, покрывающих все 1 (0) функции, образуют тупико-
вую ДНФ (КНФ).
7. В элементарной конъюнкции (дизъюнкции), которая соответствует одному
контуру, остаются только те переменные, значение которых не изменяется
внутри обведенного контура.
Примечание:
• Переменные булевой функции входят в элементарную коньюнкцию (для
значений функции 1) без инверсии, если их значение на соответствующих
координатах равно 1, и с инверсией — если 0.
• Для значений булевой функции, равных 0, записываются элементарные дизъ-
юнкции, куда переменные входят без инверсии, если их значение на соот-
ветствующих координатах равно 0, и с инверсией — если 1.
. . . . . . . . . . . . . . . . . . . . . .
Пример 4.14
. . . . . . . . . . . . . . . . . . . . .
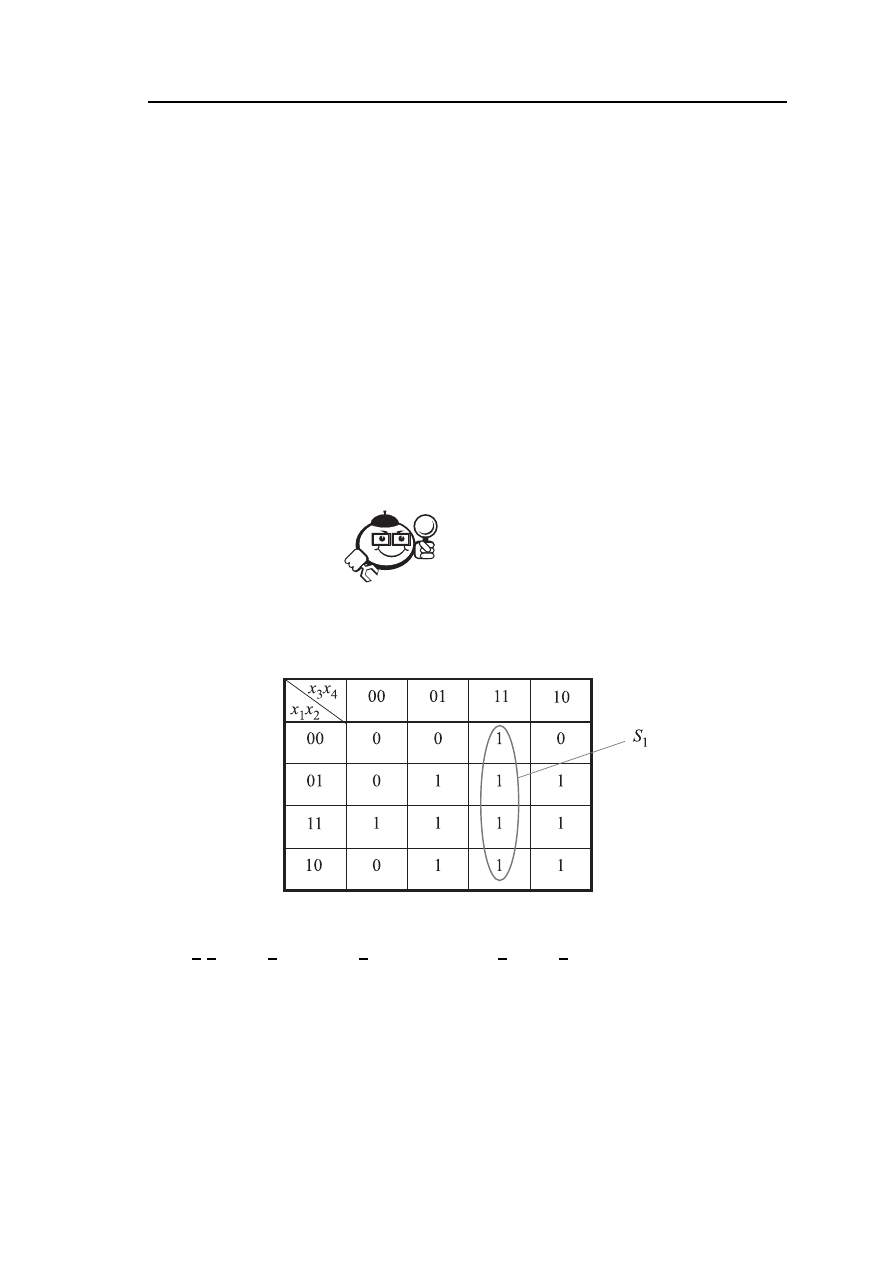
В соответствии с правилами минимизации БФ с использованием карт Карно,
требуется выделить группы единиц с помощью контуров.
Выделим первый контур S
1
с единицами:
Для выделенного контура S
1
запишем функцию F
1
в форме СДНФ:
F
1
= x
1
x
2
x
3
x
4
+
x
1
x
2
x
3
x
4
+
x
1
x
2
x
3
x
4
+
x
1
x
2
x
3
x
4
= x
1
x
3
x
4
+
x
2
x
3
x
4
+
x
1
x
3
x
4
+
x
2
x
3
x
4
= x
3
x
4
.
Запишем импликанту функции F
1
:
F
1
= x
3
x
4
.
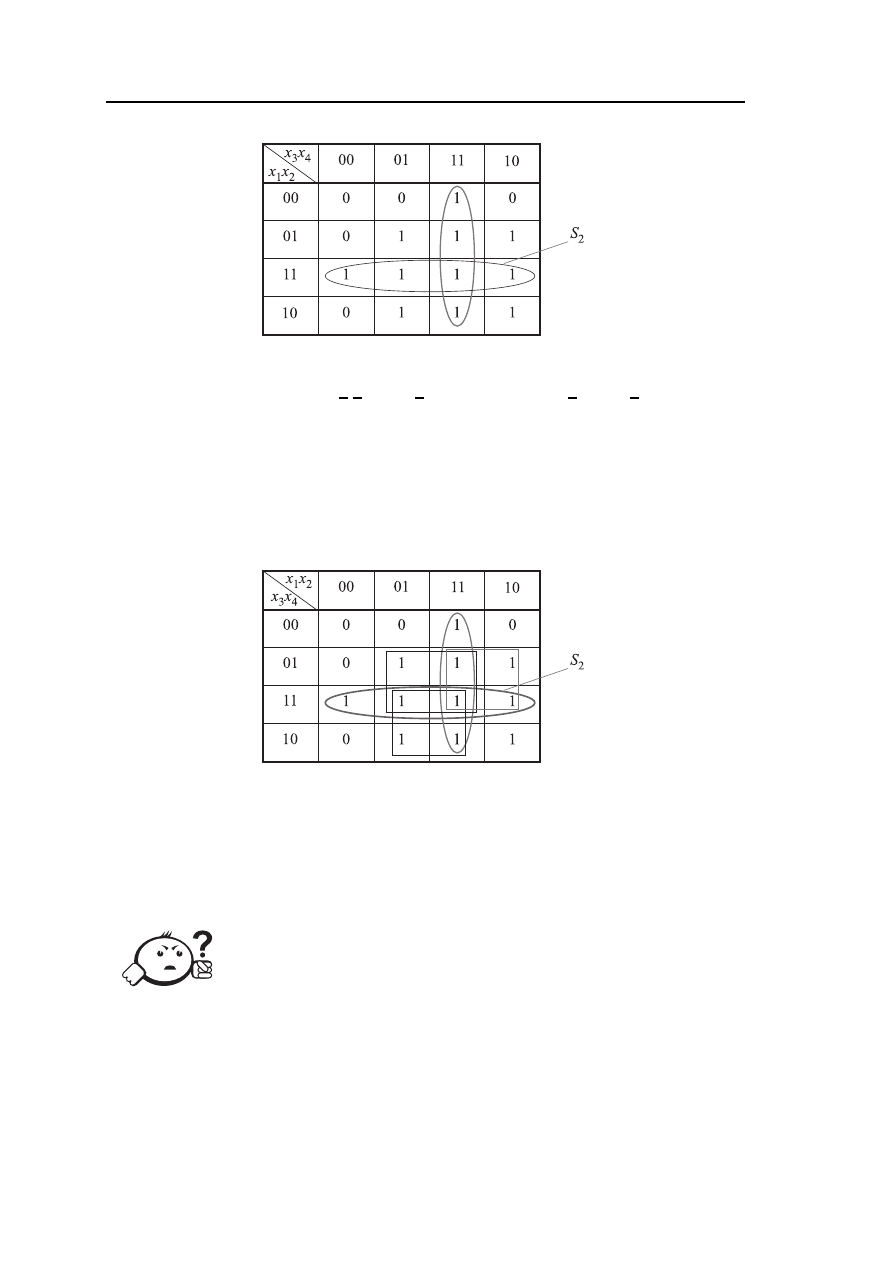
Выделим второй контур с единицами:
82
Глава 4. Переключательные функции
Для выделенного контура S
2
запишем функцию F
2
в форме СДНФ:
F
2
= x
1
x
2
x
3
x
4
∨
x
1
x
2
x
3
x
4
∨
x
1
x
2
x
3
x
4
∨
x
1
x
2
x
3
x
4
= x
1
x
2
x
3
∨
x
1
x
2
x
4
∨
∨
x
1
x
2
x
3
∨
x
1
x
2
x
4
= x
1
x
2
∨
x
1
x
2
= x
1
x
2
.
Выделим импликанту функции F
2
:
F
2
= x
1
x
2
.
Продолжая процедуру выделения контуров до тех пор, пока это возможно,
получим в итоге шесть контуров, отвечающих сформулированным выше требованиям:
Минимальная функция F будет иметь вид:
F
= F
1
∨
F
2
∨
F
3
∨
F
4
∨
F
5
∨
F
6
= x
3
x
4
∨
x
1
x
2
∨
x
2
x
4
∨
x
1
x
4
∨
x
1
x
3
∨
x
2
x
3
.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Контрольные вопросы по главе 4
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1. Какая функция называется переключательной?
2. Какая функция называется булевой?
3. Способы задания булевых функций.
4. Методы минимизации булевых функций.
5. Основные законы булевой алгебры.

Глава 5
КОМБИНАТОРИКА
Комбинаторика, или комбинаторный анализ, — это раздел математики, посвя-
щенный решению задач выбора и расположения элементов некоторого, обычно
конечного, множества в соответствии с заданными правилами. Каждое такое пра-
вило определяет способ построения некоторой конфигурации из элементов исход-
ного множества, называемой комбинаторной конфигурацией. Можно сказать, что
целью комбинаторного анализа является изучение комбинаторных конфигураций,
в частности вопросы их существования, алгоритмы построения, решение задач на
перечисление. Примерами комбинаторных конфигураций являются перестановки,
размещения и сочетания; блок-схемы и латинские квадраты.
Возникновение основных понятий и развитие комбинаторики шло параллельно
с развитием других разделов математики (алгебры, теории чисел, теории вероят-
ностей), с которыми комбинаторный анализ тесно связан. Математикам Древне-
го Востока были известны: формула, выражающая число сочетаний через бино-
минальные коэффициенты, и формула бинома Ньютона с натуральным показате-
лем n. Рождение комбинаторного анализа как раздела математики связано с труда-
ми Б. Паскаля и П. Ферми по теории азартных игр. Эти труды, составившие основу
теории вероятностей, одновременно содержали принципы определения числа ком-
бинаций элементов конечного множества.
Большой вклад в развитие комбинаторных методов был сделан Г. Лейбницем,
Я. Бернулли, Л. Эйлером. С 50-х годов прошлого столетия интерес к комбинатори-
ке возродился благодаря бурному развитию кибернетики, дискретной математики,
теории планирования, информатики. В теории вероятностей формулы комбинато-
рики широко используются для подсчета числа исходов опыта.

84
Глава 5. Комбинаторика
5.1 Основные формулы комбинаторики
Основной принцип комбинаторики.
Пусть требуется выполнить одно за другим k действий, причем первое дей-
ствие можно выполнить P
1
способами, второе — P
2
способами и т. д., тогда все
k действий можно выполнить следующим числом способов
P
= P
1
⋅
P
2
⋅
. . . ⋅ P
k
.
Все базовые формулы комбинаторики выводятся как следствия из этого основ-
ного правила.
Сочетания.
Пусть W — множество из n элементов. Произвольное (неупорядоченное) k-эле-
ментное подмножество множества из n элементов называется сочетанием из n эле-
ментов по k. Например, сочетаниями из трёх элементов по два являются следую-
щие неупорядоченные подмножества множества
{a,b,c}: {a,b},{a,c},{b,c}.
Число сочетаний из n элементов по k вычисляется по формуле:
C
k
n
=
n!
k!
(n − k)!
.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Множество называется упорядоченным, если каждому элементу
этого множества поставлено в соответствие некоторое число (но-
мер элемента) от 1 до n (n — число элементов множества) так,
что различным элементам соответствуют различные числа. Вся-
кое конечное множество можно сделать упорядоченным, если, на-
пример, переписать все элементы множества в некоторый список
(a, b, c, . . .), а затем поставить в соответствие каждому элементу
номер места, на котором он стоит в списке. Очевидно, что каж-
дое множество, содержащее более одного элемента, можно упо-
рядочить не единственным способом. Упорядоченные множества
считаются различными, если они отличаются либо своими элемен-
тами, либо их порядком.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Перестановки.
Различные упорядоченные множества, которые отличаются лишь порядком
элементов (т. е. могут быть получены из того же самого множества), называются
перестановками этого множества. Например, перестановками множества A
=
{a,b,c}
являются упорядоченные множества
(a,b,c),(a,c,b),(b,a,c),(b,c,a),(c,a,b), (c, b,a).
Найдем число различных способов, которыми может быть упорядочено дан-
ное множество, т. е. число перестановок множества A. Пусть множество A имеет
n элементов. Обозначим число его перестановок через P
n
. Число перестановок из
n элементов равно
P
n
= n!.

5.1 Основные формулы комбинаторики
85
Доказательство 1. Выберем некоторый элемент a из множества A. Рассмотрим
все перестановки, в которых a имеет номер 1. Число таких перестановок будет
равно числу перестановок из n−1 элементов множества A, которые остаются после
исключения из множества элемента a. Поэтому число перестановок, для которых
a имеет номер 1, равно P
n
−1
. Обозначим через M множество всех перестановок
множества A, а через M
a
— множество перестановок, в которых a имеет номер 1.
Тогда
M
= M
a
∪
M
b
∪
. . . ∪ M
f
,
где a, b, . . ., f — все элементы множества A. Поскольку никакие 2 множества из мно-
жеств M
a
, M
b
, . . ., M
f
не имеют общих элементов (напомним, что элементы этих
множеств — перестановки, в различных множествах на первом месте стоят различ-
ные элементы, следовательно, и соответствующие перестановки будут различны-
ми), то N
(M) = N(M
a
) + N(M
b
) + ... + N(M
f
). Следовательно,
P
n
= n ⋅ P
n
−1
= n!.
Доказательство 2. Будем последовательно выбирать элементы множества A
и размещать их в определенном порядке на n местах. На первое место можно
поставить любой из n элементов. После того как заполнено первое место, на второе
место можно поставить любой из оставшихся n − 1 элементов и т. д. По правилу
умножения все n мест можно заполнить n
(n − 1)(n − 2)...2 ⋅ 1 = n! способами.
Следовательно, множество A из n элементов можно упорядочить n! способами:
P
(n) = 1 ⋅ 2 ⋅ ... ⋅ (n − 1)n = n!
Размещения.
Упорядоченное k-элементное подмножество множества из n элементов называ-
ется размещением из n элементов по k. Например, размещениями из трёх элемен-
тов по два являются следующие упорядоченные подмножества множества
(a,b,c):
(a,b),(b,a),(a,c),(c,a),(b,c),(c,b). Число размещений из n элементов по k равно
A
k
n
= k! ⋅ C
k
n
=
n!
(n − k)! =
n
(n − 1)...(n − k + 1).
Числа размещений, перестановок и сочетаний связаны равенством
A
mn
= P
m
C
mn
.
Замечание. Выше предполагалось, что все n элементов различны. Если же
некоторые элементы повторяются, то в этом случае комбинации с повторения-
ми вычисляют по другим формулам. Например, если среди n элементов есть n
1
элементов одного вида, n
2
элементов другого вида и т. д., то число перестановок
с повторениями
P
n
(n
1
, n
2
, . . .
) =
n!
(n
1
!n
2
!. . .
)
,
где n
1
+
n
2
+
. . .
= n.