ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 5098
Скачиваний: 30
51
1
1
0
0
0
5
1
0
1
0
0
4
0
1
0
1
0
3
0
0
1
0
1
2
0
0
0
1
1
1
5
4
3
2
1
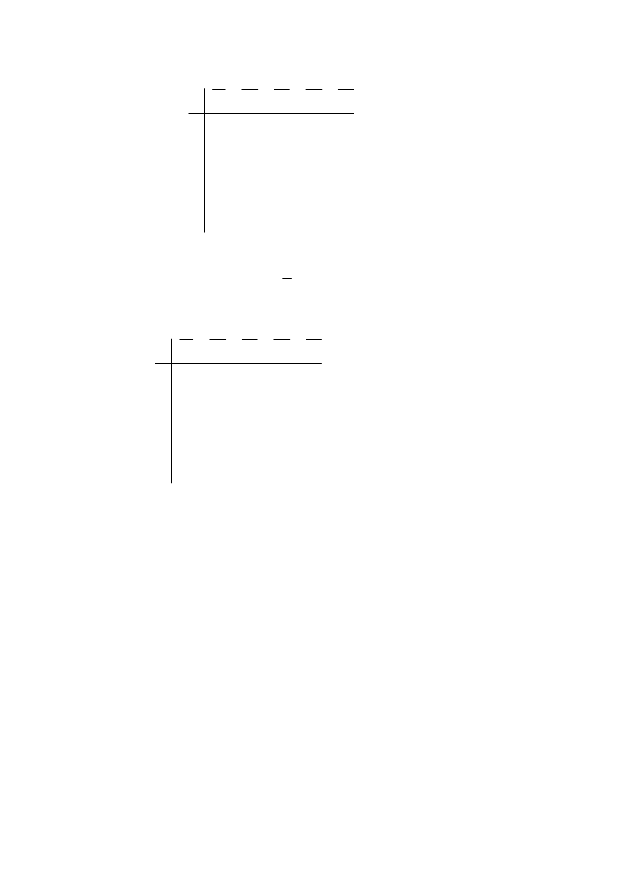
u
u
u
u
u
A
=
ш.3. Введём новые логические переменные х
1,
х
2,
х
3,
х
4,
х
5
(по числу вершин в графе L ) и из матрицы А образуем матри-
цу Ах
:
5
5
4
4
3
3
2
2
0
0
0
5
0
0
0
4
0
0
0
3
0
0
0
2
0
0
0
1
1
1
5
4
3
2
1
x
x
x
x
x
x
x
x
x
x
u
u
u
u
u
Ax
=
ш.4. Составляем произведение П
L
)
5
4
)(
5
3
)(
4
2
)(
3
1
)(
2
1
(
x
x
x
x
x
x
x
x
x
x
L
П
+
+
+
+
+
=
ш.5. Преобразуем выражения П
L
к минимальной форме:
)
5
4
)(
5
3
)(
4
2
)(
3
1
)(
2
1
(
x
x
x
x
x
x
x
x
x
x
L
П
+
+
+
+
+
=
=
(перемножаем скобки первую со второй и третью с пятой)
=
)
5
3
)(
5
2
4
)(
3
2
1
(
x
x
x
x
x
x
x
x
+
+
+
=
(перемножаем скобки первую со второй)
)
5
3
)(
5
3
2
4
3
2
5
2
1
4
1
(
x
x
x
x
x
x
x
x
x
x
x
x
x
+
+
+
+
=
=
(перемножаем скобки первую со второй)
=
+
+
+
+
+
+
+
+
=
5
3
2
5
3
2
5
4
3
2
4
3
2
5
2
1
5
3
2
1
5
4
1
4
3
1
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
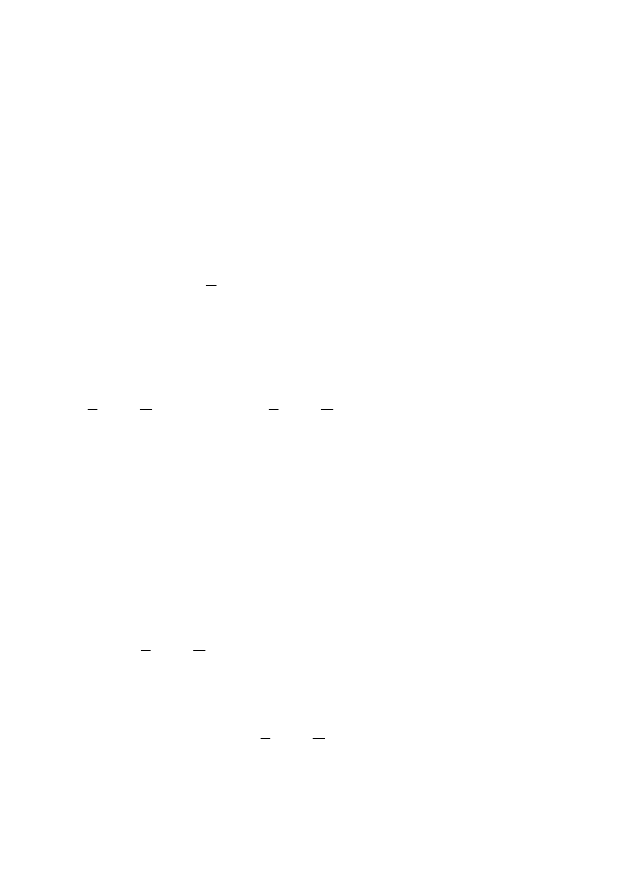
52
(применяем законы, указанные в п.п. 3,5 данного пособия)
=
5
3
2
4
3
2
5
2
1
5
4
1
4
3
1
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
+
+
+
+
.
Преобразование выражения П
L
закончено. Получена мини-
мальная форма-полином
∑L .
ш.6. Выделим для каждого слагаемого полинома
∑L =
5
3
2
4
3
2
5
2
1
5
4
1
4
3
1
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
+
+
+
+
его дополнение до множества переменных {x
1
,x
2
, x
3
, x
4
, x
5
}:
(x
2
x
5
); (x
2
,x
3
); (x
3
,x
4
); (x
1
,x
5
); (x
1
,x
4
);
полученные дополнения порождают максимальные пустые
подграфы графа
L
и заданного графа L .
Алгоритм Х. Магу и Дж. Уэйсмана может быть применён и
для выявления в графе L=(X,U; P) общего вида всех максималь-
ных полных (плотных) подграфов. Для этого необходимо по-
строить для заданного графа
)
;
,
(
P
U
X
L
=
его скелет – граф
)
,
(
U
X
L
=
, а для графа
)
,
(
U
X
L
=
построить дополнительный
граф
)
*
,
(
*
U
X
L
=
(определение дополнительного графа дано в
теме 1 данного методического пособия). Получить дополни-
тельный граф легко, если исходный граф задать матрицей смеж-
ности его вершин, в которой всем элементам, равным нулю,
присвоить значение «1», а всем элементам, значения которых не
равны нулю, присвоить значение «0».
Далее для полученного графа
)
*
,
(
*
U
X
L
=
с помощью ал-
горитма Х. Магу и Дж. Уэйсмана (рассмотренного выше) выяв-
ляем все максимальные пустые подграфы. Эти подграфы явля-
ются максимальными полными (плотными) подграфами для
графов
)
,
(
U
X
L
=
и
)
;
,
(
P
U
X
L
=
.
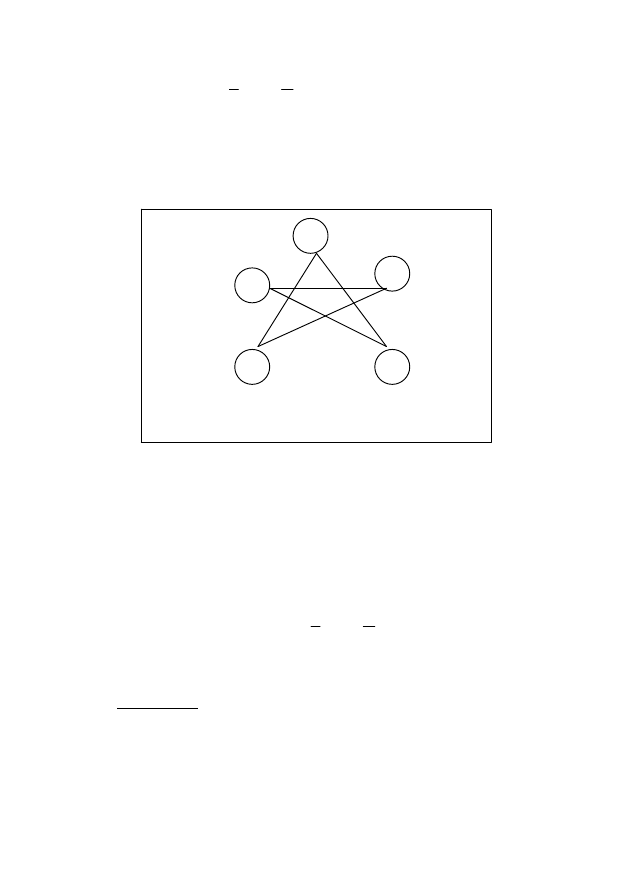
ПРИМЕР. В графе
)
;
,
(
P
U
X
L
=
, представленном на рисун-
ке 1, выделить все максимальные полные(плотные) подграфы.
ш.1. Строим скелет
)
,
(
U
X
L
=
(рисунок 2) графа L .
53
ш.2. Для графа
)
,
(
U
X
L
=
строим его дополнительный граф
)
*
,
(
*
U
X
L
=
(рисунок 3), в котором с помощью алгоритма
Х.Магу
−Дж.Уэйсмана выявляем максимальные пустые подгра-
фы.
*
1
u
*
2
u
*
5
u
*
3
u
*
4
u
1
2
3
5
4
Рисунок 3
Приведём окончательный результат решения данной задачи
− полином
∑L =
5
4
3
5
4
2
5
3
1
4
2
1
3
2
1
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
+
+
+
+
и дополнения для его слагаемых: (
5
4
x
x
); (
5
3
x
x
); (
4
2
x
x
);
(
3
1
x
x
); (
2
1
x
x
), которые порождают все максимальные пустые
подграфы графа
)
*
,
(
*
U
X
L
=
и максимальные полные (плот-
ные) подграфы графа
)
,
(
U
X
L
=
и заданного графа
)
;
,
(
P
U
X
L
=
.
ЗАДАНИЕ
На графе своего варианта выделить все максимальные
пустые и максимальные полные (плотные) подграфы, с по-
мощью алгоритма Х.Магу
−
Дж.Уэйсмана, и привести их гео-
метрическое представление.

54

55