ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 5101
Скачиваний: 30

46
2. Радиус графа определяется по матрице метрики сле-
дующим способом: в каждой строке матрицы М выделяется
максимальный элемент. Минимальный элемент из этих макси-
мальных и есть радиус графа.
3. Диаметр графа определяется по матрице метрики сле-
дующим способом: в каждой строке матрицы М выделяется
максимальный элемент. Максимальный элемент из этих макси-
мальных и есть диаметр графа.
ЗАДАНИЕ
1. Построить метрику графа для своего варианта индивиду-
ального задания.
2. Вычислить радиус, диаметр данного графа.
3. Найти все периферийные и центральные вершины графа.

47
Тема
5.
СТРУКТУРНЫЙ
АНАЛИЗ
ГРАФОВ
Задача структурного анализа графов является одной из
центральных задач теории графов и имеет широкое применение
при решении фундаментальных теоретических проблем в про-
граммировании и прикладных задачах при анализе объектов
математических моделей.
Данная задача связана с базовыми понятиями: связность
графа; компонента связности графа, число компонент связности,
полный ( плотный) граф, максимальные полные и максимальные
пустые подграфы, скелет графа, определения которых и теоре-
тические выкладки даны в учебном пособии «Дискретная ма-
тематика. Часть 2» (автор Е.Ф. Жигалова), а также в темах 1, 3
данных методических указаний.
В данной теме мы более подробно рассмотрим алгоритмы
для нахождения всех максимальных пустых и максимальных
полных подграфов в заданном графе общего вида.
Определение: а) подграф называется максимальным пус-
тым подграфом графа L=(X,U;P), если он не является подгра-
фом никакого большего максимального пустого подграфа за-
данного графа;
б) подграф называется максимальным полным подграфом
графа L=(X,U;P), если он не является подграфом никакого
большего максимального полного подграфа заданного графа.
Легко доказать, что задача выявления максимальных пол-
ных (плотных) и максимальных пустых подграфов в заданном
графе
)
;
,
(
P
U
X
L
=
общего вида легко сводится к случаю обык-
новенных графов. Поэтому, для практического выявления всех
максимальных полных и пустых подграфов в произвольном
графе, достаточно уметь выявлять только максимальные плот-
ные и пустые подграфы обыкновенных графов.
Приведём алгоритм выявления всех максимальных пустых
подграфов в заданном графе общего вида, основанный на рабо-
тах Х. Магу и Дж. Уэйсмана:
п.1.Для графа L=(X,U;P) общего вида построим его скелет
)
,
(
U
X
L
=
( смотри тему 1 данного методического пособия).

48
п.2. Построим матрицу инциденций А графа
)
,
(
U
X
L
=
,
элементы которой a
i,j
принимают значения 0 либо 1 (
n
i
,
1
=
;
m
j
,
1
=
, где n =
⏐
X
⏐
−
число вершин в
)
,
(
U
X
L
=
, m =
⏐
U
⏐−
число рёбер в
)
,
(
U
X
L
=
).
п.3. Дополним систему логическими переменными х
1
, х
2
, …,
х
i
, …, х
n
, которые принимают значения 0 и 1, и подчиним её
условиям:
i
x
i
x
=
2
;
1
1
=
+
i
x
;
i
x
i
x
i
x
=
+
, 1+1=1, т.е. 2=1, (i=1,2,…,n),
а также законам коммутативности, ассоциативности и дистри-
бутивности.
п.4.
Из матрицы инциденций
⎟⎟
⎟
⎟
⎟
⎠
⎞
⎜⎜
⎜
⎜
⎜
⎝
⎛
=
nm
n
n
m
m
a
a
a
a
a
a
a
a
a
A
...
.
.
.
.
...
...
2
1
2
22
21
1
12
11
графа
)
,
(
U
X
L
=
, где n ,m соответственно равны числу вершин
и рёбер графа, образуем матрицу
⎟⎟
⎟
⎟
⎟
⎠
⎞
⎜⎜
⎜
⎜
⎜
⎝
⎛
=
n
nm
n
n
n
n
m
x
a
x
a
x
a
x
a
x
a
x
a
x
a
x
a
x
a
Ax
...
.
.
.
.
...
...
2
1
2
2
2
22
2
21
1
12
1
12
1
11
и составим произведение
i
x
n
i
ij
a
m
j
П
n
x
x
x
L
П
L
П
∑
=
=
=
=
1
1
)
,...,
2
,
1
(
Очевидно, что j-й сомножитель произведения
L
П есть
сумма двух слагаемых, соответствующих тем двум вершинам,
которые в графе соединены j-м ребром.
п.5. Преобразуем произведение
L
П к бесскобочному виду
и привести всю сумму к минимальной форме, пользуясь дист-
рибутивным, ассоциативным, коммутативным законами и при-
меняя закон поглощения: а) а+ав =а; б) (а+в)(а+с)
…
(а+р) =
49
=а+вс
…
р, где а,в,с,…,р
− логические переменные, принимающие
значения 0;1, выполняя при этом условия, описанные в п.3.
В результате выполненных преобразований выражение
L
П
будет иметь минимальную форму и представлять сумму произ-
ведений переменных из множества х
1
, х
2
, …,х
i
,…,х
n ,
т.е. много-
член. Обозначим его
∑
L
.
п.6. Для каждого слагаемого многочлена
∑
L
выделим пе-
ременные, которые в него не входят, но входят в множество {х
1
,
х
2
, …, х
i
, …, х
n
}. Эти переменные порождают максимальные
пустые подграфы данного графа L, так как соответствующие им
вершины графа L образуют максимальные пустые подграфы.
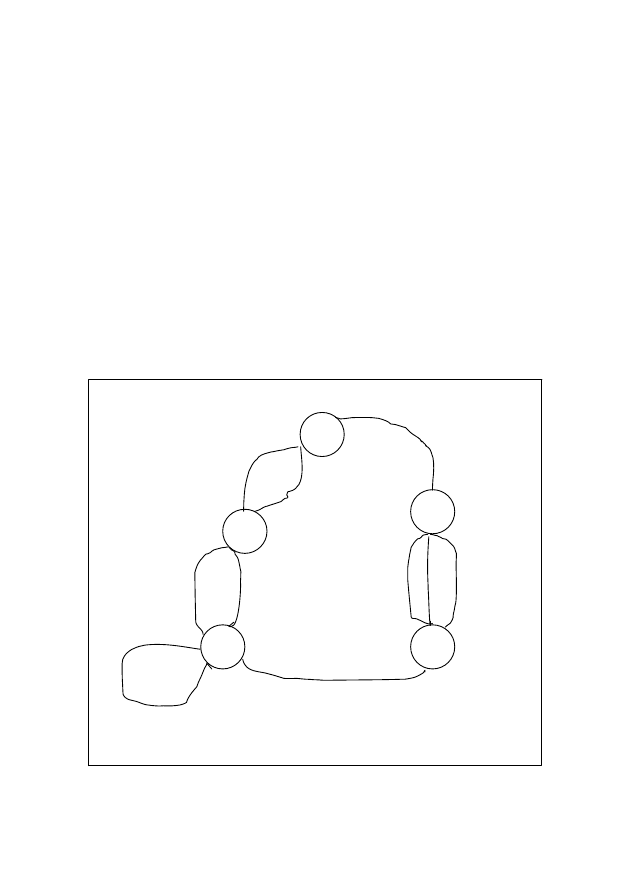
ПРИМЕР. В графе
)
;
,
(
P
U
X
L
=
, представленном на рисун-
ке 1, выделить все максимальные пустые подграфы.
u1
u2
u3
u4 u9
u5 u8
u10
u 6
u7
1
2
3
4
5
Рисунок 1
50
Матрица смежности B графа L содержит элементы
(
ij
b
),
5
,
1
;
5
,
1
=
=
j
i
, равные:
b
11
= b
22
= b
33
= b
55
=0; b
44
=1; b
12
=2; b
13
=1; b
14
=0; b
15
= 0;
b
21
=2; b
23
=0; b
24
=2; b
25
= 0; b
31
=1; b
32
=0; b
34
=0; b
35
= 3;
b
41
=0; b
42
=2; b
43
=0; b
45
= 1; b
51
=0; b
52
=0; b
53
=3; b
54
= 1;
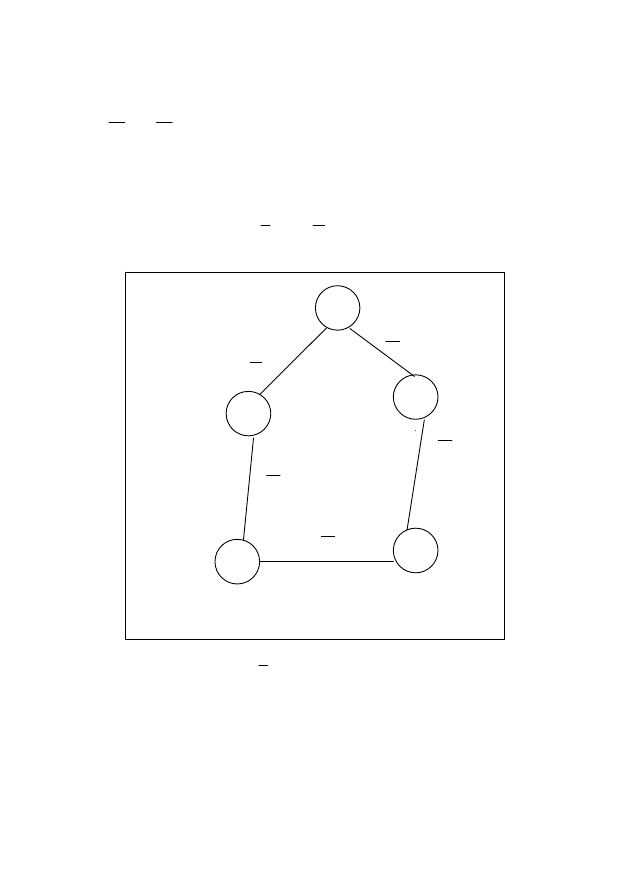
ш.1. Строим скелет
)
,
(
U
X
L
=
(рисунок 2) графа L .
2
u
1
u
4
u
3
u
5
u
3
4
1
2
5
Рисунок 2
ш.2. Для графа L определим его матрицу инциденций
А: