ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 5094
Скачиваний: 30
31
ся матрицей смежности, если её строки и столбцы соответст-
вуют вершинам графа, а элементы r
i,j
образуются по правилу:
- r
i,j
= 1, если вершина x
i
соединена с вершиной x
j
ребром,
т.е. x
i
смежна x
j
;
- r
i,j
= 0 в противном случае.
Заметим, что для мультиграфа и смешанного графа задают:
- r
i,j
= p, если вершина x
i
соединена с вершиной x
j
p – чис-
лом рёбер;
- r
i,j
= 0 в противном случае.
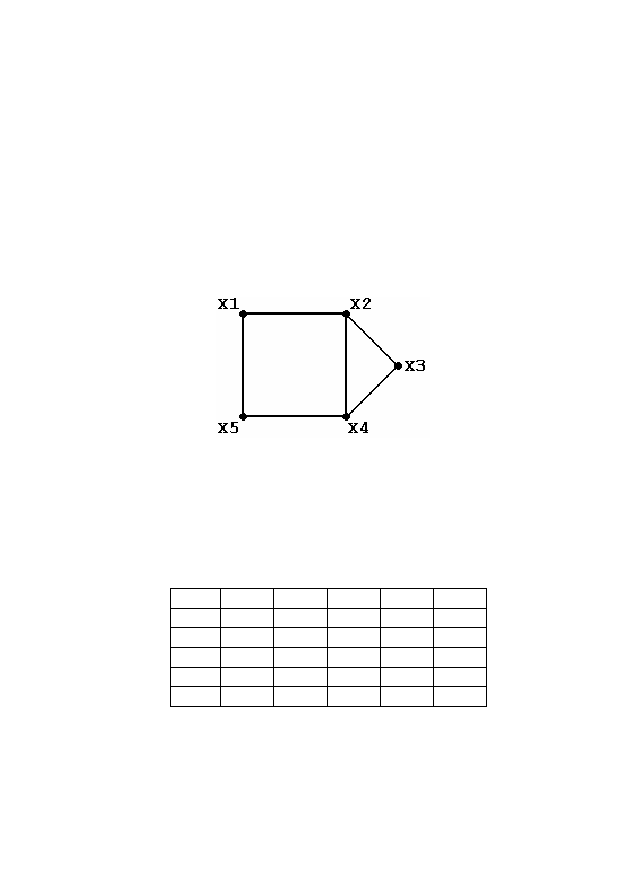
Рисунок 1
Очевидно, что для неорграфов r
i,j
= r
j,i
и для их задания
можно использовать треугольную матрицу R. Так, для графа на
рисунке 1 матрица смежности R имеет вид:
R =
X1 X2 X3 X4 X5
X1
0 1 0 0 1
X2
1 0 1 1 0
X3
0 1 0 1 0
X4
0 1 1 0 1
X5
1 0 0 1 0
Треугольная матрица R’ для этого же графа запишется
32
R
’
=
X1 X2 X3 X4 X5
X1
0 1 0 0 1
X2
0 1 1 0
X3
0
1
0
X4
0
1
X5
0
Строки и столбцы матрицы R cоответствуют вершинам
графа. На пересечении i-й строки и j-го столбца ставится эле-
мент r
i,j
, соответствующий числу рёбер, соединяющих вершины
x
i
и x
j
. Строки и столбцы матрицы R можно нумеровать числа-
ми натурального ряда, соответствующими индексам помечен-
ных вершин. Петлям в графе соответствуют элементы r
i,i
глав-
ной диагонали матрицы R. Преимущесво использования матриц
смежности – это простота выполнения преобразований и опера-
ций над графами как для конструктора, так и для ЭВМ.
1.3.3.2 Граф можно задавать также матрицей инциденций B,
строки которой соответствуют вершинам графа, столбцы – реб-
рам. Элементы b
i,j
матрицы B для неорграфа могут принимать
значения ( 0 или 1 ):
b
i,j
= 1, если ребро u
k
инцидентно вершине x
i
;
b
i,j
= 0, если ребро u
k
неинцидентно вершине x
i
.
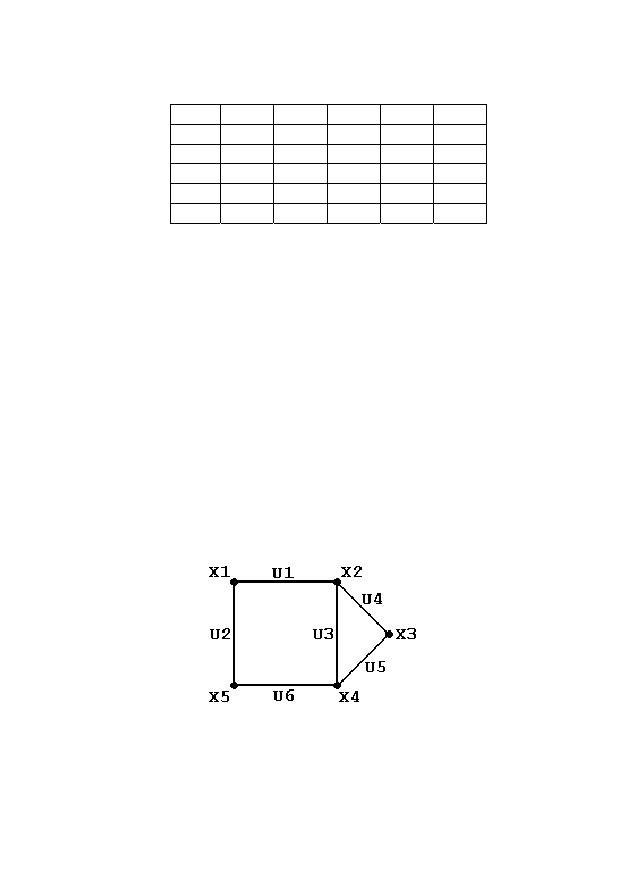
Рисунок 2
Для графа, представленного на рисунке 2, матрица инци-
денций B имеет вид:

33
U1 U2 U3 U4 U5 U6
X1
1 1 0 0 0 0
X2
1 0 1 1 0 0
X3
0 0 0 1 1 0
X4
0 0 1 0 1 1
X5
0 1 0 0 0 1
1.4
Числовые
характеристики
вершин
графа
Каждая вершина графа имеет числовую характеристику
s(x), которая называется степенью, или валентностью, вершины.
Степень вершины S(x
i
) это целое положительное число, равное
количеству ребер, инцидентных вершине х
i
.
Для ориентированных графрв различают «полустепени ис-
хода» и «полустепени захода». Это тоже числовые характери-
стики вершин, соответственно равные количеству дуг, исходя-
щих из вершины и входящих в вершину.
1.5
Маршруты
,
цепи
и
циклы
В этой главе будут рассмотрены такие свойства графов,
которые не меняются при произвольной ориентации звеньев
графа, переориентации или дезориентации дуг (всех или неко-
торых). Мы рассмотрим такие свойства графов общего вида
)
;
,
(
P
U
X
L
=
, которые полностью определяются предикатом
)
,
,
(
)
,
,
(
~
y
u
x
P
y
u
x
P
⇔
∨
)
,
,
(
x
u
y
P
, называемым полуинцидентором
(неоринцидентором) графа L.
О неорграфе
)
~
;
,
(
~
P
U
X
L
=
можно сказать, что он получен
из L посредством дезориентации его дуг. В свою очередь L
можно получить из L
~
ориентацией звеньев.
Определение:
Конечная последовательность M элементов графа L:
М = x
0
u
1
x
1
u
2
x
2
...x
k–1
u
k
x
k
( k >=0 ),
для которой истинно высказывание:
P'(x
0
,u
1
,x
1
) & P'(x
1
,u
2
,x
2
) & ... & P'(x
k–1
,u
k
,x
k
),

34
называется маршрутом из вершины x
0
в вершину x
k
, или мар-
шрутом, соединяющим вершину x
0
c вершиной x
k
; в случае
x
0
=x
k
имеем циклический маршрут при вершине x
0
, или цикл.
Число k носит название длины маршрута M. Иными словами,
длина маршрута равняется числу ребер, входящих в него. Заме-
тим, что маршрут – это не просто часть графа, ибо порядок его
обхода играет существенную роль; так, маршрут M1:
М1 = x
k
u
k
x
k–1
... x
2
u
2
x
1
u
1
x
0
при k>=0
не совпадает с написанным выше маршрутом М, хотя и состоит
из тех же самых элементов и с тем же отношением инцидентно-
сти.
Маршрут M:
M = x
0
u
1
x
1
u
2
x
2
... x
k–1
u
k
x
k
называется цепью, если ребра u
1
, u
2
,...,u
k
различны (при k<=1
это условие выполнено «в силу ложности посылки»). Цепь, в
случае если x
0
= x
k
, при k >= 1 называется циклом.
Цепь называется простой, если все ее вершины
x[p],x[k],...,x[l] различны.
В случае, когда x[0]=x[l] & l>=1, имеем простой цикл, ко-
торый, будучи цепью, в то же время не есть простая цепь. Цепь,
в которой начальная и конечная вершины не совпадают, но есть
повторяющиеся вершины, называется циклической.
ЛЕММА.
Всякий маршрут (в частности, всякая цепь) графа содержит
хотя бы одну простую цепь, соединяющую ту же пару вершин.
Всякий циклический маршрут нечетной длины содержит про-
стой цикл нечетной длины. Всякий цикл содержит простой
цикл.
СЛЕДСТВИЕ:
Всякий кратчайший маршрут между двумя заданными
вершинами графа есть простая цепь. Всякий цикл наименьшей
длины при заданной вершине является простым.
35
1.6
Определение
числа
маршрутов
длины
«L»
на
графе
Маршрутом
μ
i,j
в графе G=(X,U) называется конечная по-
следовательность вершин и рёбер вида –
μ
0,l
=( x
0
,u
1
,x
1
,u
2
,x
2
,...,x
l–1
,u
k
, x
l
),
где x
0
, x
l
– соответственно начальная и конечная вершины маршрута
μ
0,l
.
Очевидно, в конечном графе G=(X,U) можно выделить
только конечное число маршрутов. Длина маршрута
μ
i,j
равна
числу рёбер, которые в него входят.
Часто требуется знать, сколько маршрутов заданной длины
в графе G связывает вершину x
i
с вершиной x
j
.
Для определения маршрутов длины q в графе G=(X,U) его
матрицу смежности R возводят в степень, равную q. Тогда для
каждого значения степени q=1,2,…,k значение элемента (r
i,j
)
q
матрицы R
q
определяет количество маршрутов
μ
i,j
длиной, рав-
ной значению степени q.
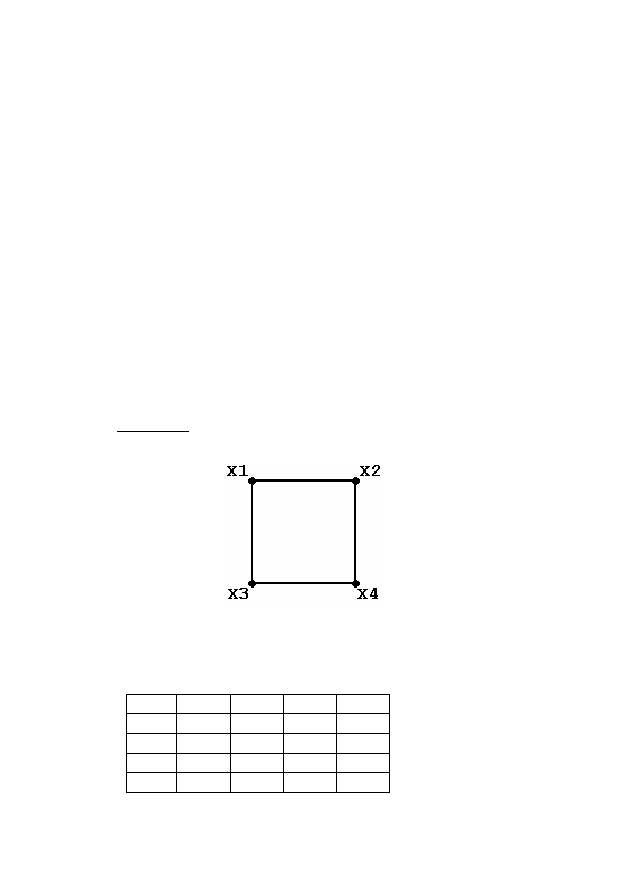
ПРИМЕР. Для графа G= (X,U) , представленного на рисун-
ке 3, определить количество маршрутов длины, равной 2.
Рисунок 3
Матрица смежности R графа G имеет вид:
R=
X1 X2 X3 X4
X1
0 1 1 0
X2
1 0 0 1
X3
1 0 0 1
X4
0 1 1 0
1
2
3
4