ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 5097
Скачиваний: 30

36
Возведем матрицу R в квадрат:
R
2
=
X1 X2 X3 X4
X1
2 0 0 2
X2
0 2 2 0
X3
0 2 2 0
X4
2 0 0 2
Значение каждого элемента r
i,j
матрицы R
2
равно числу
маршрутов длины 2, ведущих из вершины x
i
в вершину x
j
.
Например, r
3,2
=2 означает, что в графе два маршрута дли-
ны 2, которые ведут из вершины x
3
в вершину x
2
. Запишем
их:
μ
3,2
=x
3,
3,x
1
,1,x
2
;
μ
3,2
=x
3
,4,x
4
,2,x
2
.
Выполнить индивидуальное задание:
1.
Построить матрицы смежности и инциденций для графа
G=(X,U) своего варианта (рисунок 1).
2.
По матрицам, представленным на рисунках 2, 3, постро-
ить графы, предварительно определив их тип в терминах теории
графов. Определить класс построенных графов.
3.
Определить число маршрутов длины L = 3 для графа
G =(X,U) своего варианта.
4.
Построить все маршруты длины L = 3 между вершина-
ми, указанными преподавателем (помечены символом *).
5.
Произвести ориентацию (произвольно) графа своего ва-
рианта.

37
Тема
2.
УНАРНЫЕ
ОПЕРАЦИИ
НА
ГРАФЕ
2.1
Удаление
вершины
При удалении вершины удаляются все инцидентные
ей рёбра.
Пример.
В графе G = (X,U) на рисунке 1 удалить вершину
х1.
Граф G( (рисунок 2) – результат выполнения дан-
ной операции.
EMBED Word.Picture.8
Рисунок 1 Рисунок 2
2.2
Удаление
ребра
При удалении ребра инцидентные ему вершины
(
концевые) не удаляются!
Пример.
В графе G = (X,U) на рисунке 1 удалить ребро
u2.
Граф G( (рисунок 3) – результат выполнения дан-
ной операции.
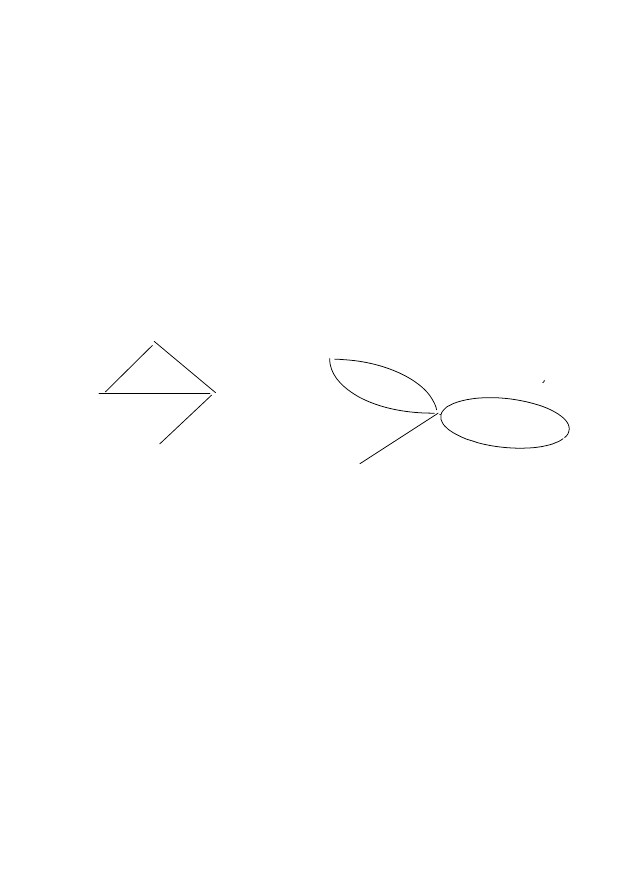
EMBED Word.Picture.8
Рисунок 3
Если из графа требуется удалить некоторое множество
вершин и рёбер, то эта процедура сводится к последовательному
удалению каждой вершины отдельно и отдельно каждого ребра.
38
2.3
Замыкание
(
отождествление
)
вершин
Для любой заданной пары вершин V
i
, V
j
операция замыка-
ния сводится к отождествлению этих вершин в новую вершину
V
k
, при этом все рёбра, инцидентные вершинам V
i
и V
j
, стано-
вятся инцидентными вершине V
k .
ПРИМЕР. На графе G=(X,U), представленном на рисунке 4,
а, выполнить операцию «замыкания» вершин x
1
и x
2.
На рисунке 4, б представлен граф G
″, полученный из графа
G после «замыкания» вершин х1 и х2, где вершина xk=(x1+x2).
G
x1
• G"
u3
u4
x3
•
u3
x3
•
u1
•
x2
⇒
u1
xk
•
u2
x4
•
u2 u4
x4
•
а)
б)
Рисунок 4
2.4
Стягивание
вершин
графа
по
ребру
Операция стягивания вершин x
i
и x
j
графа G(X,U) по ин-
цидентному им ребру u
k
включает операцию удаления ребра u
k
и операцию отождествления вершин x
i
, x
j
.
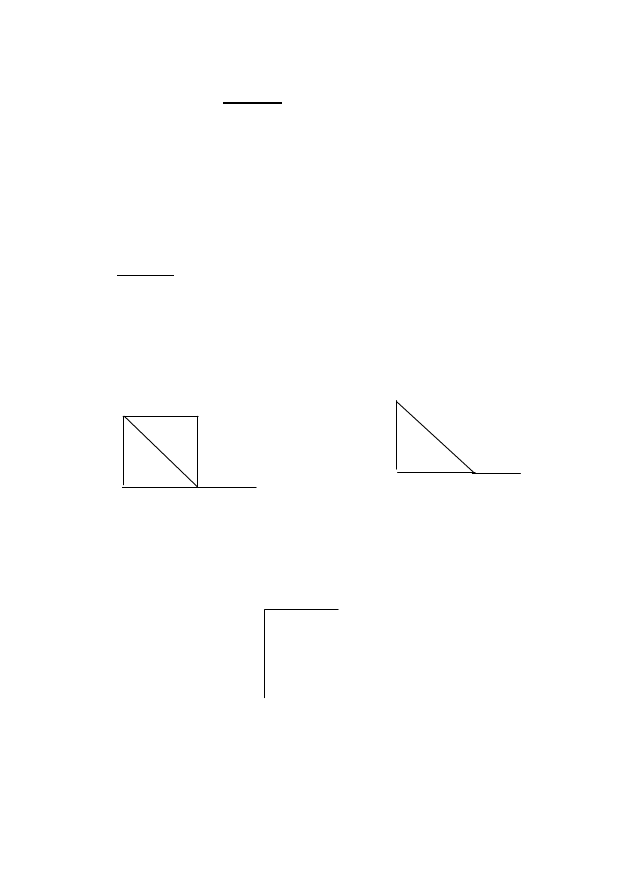
ПРИМЕР. На рисунке 5, б представлен граф G
′, получен-
ный из графа G (рисунок 5, а) операцией стягивания вершин
х3 – х2 по ребру u1.
а)
б)

39
G
G
′
x1
•
u3
u4
x1
•
u3
x3
•
u1
•
x2
⇒
u4
xk
•
u2
x4
•
u2
x4
•
а)
б)
Рисунок 5
ЗАДАНИЕ
Выполнить унарные операции на графе своего варианта.
Результат выполнения операций показать на матрицах
смежности или инциденций.
40
Тема
3.
ЧАСТИ
ГРАФА
3.1
Подграф
Граф G
′ = (Х′, U′ ) является подграфом графа G = (Х,U),
если Х
′ является подмножеством Х и U′ является подмножест-
вом U.
Пример.
1. Граф G1 (рисунок 11) является подграфом графа G (ри-
сунок 10).
2. Граф G2 (рисунок 12) является подграфом графа G (ри-
сунок 10).
G G1
x5
x5 u1 x4 o
o
о u6
u5
u5 u6 u2
u4 u3
u4 u3 o o o
o o o x1 x2 x3
x1 x2 x3
Рисунок 10 Рисунок 11
x5 x4
o
о
u5
G2
o o
x1 x3
Рисунок 12