Файл: Зотов Методичка Delphi.doc

21. Напечатать элементы массива , по абсолютной величине большие 5, и найти их сумму.

22. Поменять местами элементы массива , равноотстоящие от начала и конца массива.

23. Найти тройку последовательных элементов массива с наименьшей суммой.

24. Найти количество элементов массива , бóльших суммы элементов с четными номерами.

25. Найти наибольший элемент массива , среди тех элементов, которые меньше произведения элементов с нечетными номерами.

26. В массиве поменять местами наибольший и наименьший элементы.

27. Напечатать номера элементов массива , которые равны соответствующим элементам массива .

28. Задан массив Из его элементов сформировать два массива: и В массив включить только четные элементы массива , а в массив - только нечетные. Найти произведения элементов массивов .

29. В массиве найти номер наименьшего положительного элемента.

30. В массиве найти количество элементов, бóльших среднего арифметического значения элементов этого массива.

31. Найти номера пары элементов массива , равноотстоящих от начала и конца массива и имеющих одинаковые значения.

32. Для массивов и найти квадрат суммы произведений элементов с одинаковыми номерами и произведение сумм квадратов элементов каждого массива.

---

ЛАБОРАТОРНАЯ РАБОТА 6. ЦИКЛИЧЕСКАЯ ОБРАБОТКА ДВУМЕРНЫХ МАССИВОВ

Цель работы: приобретение практических навыков составления и отладки программ обработки двумерных массивов.

Задания

Общая постановка задачи:

Разработать алгоритм и программу решения задачи обработки двумерного массива (массивов). Размеры массива (массивов) являются входными параметрами и вводятся в программе. При работе программы исходные массивы не должны быть изменены.

Программа должна предлагать пользователю различные варианты задания значений элементов исходного массива (массивов):

1. Элементы исходного массива (массивов) вводятся пользователем.

2. Элементы исходного массива (массивов) вычисляются случайно.

3. Элементы исходного массива (массивов) задаются как предусмотренный в программе набор констант.

Варианты:

1. Вычислить сумму элементов каждой строки матрицы , определить наименьшее значение этих сумм и номер соответствующей строки.

2. Переписать положительные элементы главной диагонали матрицы в одномерный массив y, расположив их в порядке возрастания.

3. В матрице поменять местами строки с наибольшей и наименьшей суммой.

4. Найти наибольшие элементы каждой строки матрицы и записать их в массив z.

5. Найти среднее арифметическое положительных элементов каждого столбца матрицы при условии, что в каждом столбце есть хотя бы один положительный элемент. Результаты запомнить в массиве .

6. Определить количество положительных, отрицательных и нулевых элементов матрицы . Эту информацию записать в массив .

7. Найти наименьший элемент матрицы и номер строки и столбца, в которых он находится. Эту строку заполнить значениями наибольшего элемента матрицы.

8. Переписать первые положительные элементы каждой строки матрицы в массив y, а первые отрицательные элементы - в массив . Если в строке нет положительного или отрицательного элемента, то следует записать в соответствующий массив ноль.

9. Задана матрица Вычислить матрицу отличающуюся от матрицы дополнительным столбцом, каждый элемент которого равен количеству положительных элементов соответствующей строки матрицы .

10. Вычислить среднее геометрическое положительных элементов каждого столбца матрицы . Результаты записать в массив . Если в столбце нет положительного элемента, то записать в массив ноль.

11. В матрице найти количество элементов каждой строки, соответствующих неравенству . Результаты записать в массив . Если в строке нет соответствующих элементов, то записать в массив ноль.

12. Найти наименьший элемент матрицы и записать нули в ту строку и столбец, где он находится.

13. Найти минимальные элементы каждой строки матрицы и поместить их на главную диагональ, а диагональные элементы записать на место минимальных.

14. Найти среднее арифметическое положительных элементов каждого столбца матрицы при условии, что есть хотя бы один положительный элемент. Результаты записать в массив .

---

15. Переписать первые элементы каждой строки матрицы , бóльшие некоторого числа , в массив . Если в строке нет элемента, бóльшего c, то записать в массив b ноль.

16. Задана матрица . Сформировать матрицу , имеющую на один столбец больше, чем . Элементы с одинаковыми номерами у матриц и должны быть равными Дополнительный столбец должен содержать минимальные элементы строк матрицы .

17. Задана матрица . Сформировать матрицу путем вычеркивания из матрицы a третьей строки и третьего столбца.

18. Заданы матрицы и . Сравнить их соответствующие элементы (с одинаковыми номерами) и записать равные элементы в вектор .

19. Вычислить количество положительных и отрицательных элементов каждой строки матрицы . Записать эту информацию в два вектора: и

20. Найти количество элементов матрицы , значения которых принадлежат отрезку [-2; 2] и записать их номера в массив .

21. Задана матрица . Напечатать номер столбца, имеющего наибольшую сумму элементов.

22. Задана матрица . Определить номер строки, имеющей наименьшее произведение элементов.

23. Заданы матрицы и . Заменить главную диагональ матрицы на главную диагональ матрицы и наоборот.

24. В матрице найти сумму положительных элементов каждой строки и записать эти суммы в массив .

25. В матрице найти произведение модулей элементов каждого столбца. Записать эти произведения в массив

26. В матрице найти среднее арифметическое наименьших элементов каждого столбца.

27. В квадратной матрице найти сумму всех элементов, лежащих выше главной диагонали.

28. Задана квадратная матрица . Определить, является ли она симметричной относительно главной диагонали.

29. Задана матрица . Получить транспонированную к ней матрицу .

30. В квадратной матрице заменить элементы главной диагонали на максимальные элементы каждого столбца.

---

ЛАБОРАТОРНАЯ РАБОТА 7. ПОДПРОГРАММЫ. ИСПОЛЬЗОВАНИЕ ФУНКЦИЙ

Цель работы: приобретение практических навыков составления и использования подпрограмм-функций.

Задания

Общая постановка задачи:

Разработать подпрограмму-функцию для вычисления суммы ряда . Передача аргумента в функцию должна осуществляться через аппарат формальных и фактических параметров.

Используя разработанную функцию, выполнить следующее:

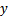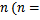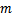1. Рассчитать значения для разных значений аргумента 1, 2, 3, …, ), где 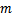- заданное целое число.

2. Напечатать результаты в виде таблицы.

3. Построить график функции 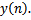На этом же графике показать контрольное математическое значение.

4. Для заданной точности 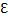определить необходимое количество слагаемых ряда.

Варианты:

	Функция	Контрольное математическое значение
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

ЛАБОРАТОРНАЯ РАБОТА 8. ПОДПРОГРАММЫ. ИСПОЛЬЗОВАНИЕ ПРОЦЕДУР

Цель работы: приобретение практических навыков составления и использования подпрограмм-процедур.

Задания

Общая постановка задачи:

Разработать алгоритм и программу решения задачи с использованием процедуры. Передача информации в процедуру должна осуществляться через аппарат формальных и фактических параметров.

Варианты:

1. Заданы числа a, b, c, d. Решить четыре уравнения:

Вещественные корни данных уравнений напечатать в порядке возрастания. Вычисление корней квадратного уравнения оформить в виде подпрограммы.

2. Четыре точки заданы своими координатами Вычислить, какие из них находятся на максимальном расстоянии друг от друга, вывести на печать значение этого расстояния.

Вычисление расстояния между двумя произвольными точками оформить в виде подпрограммы. Расстояния между любыми двумя точками и определяется по формуле .

3. Заданы длины а, b, c сторон исходного треугольника. Найти медианы такого треугольника, сторонами которого являются медианы исходного треугольника. Вычисление медиан треугольника оформить в виде подпрограммы. Медиана, проведенная к стороне а, равна .

4. Заданы стороны двух треугольников: а, b, c (∆АВС) и p, l, f (∆PLF). Переменной S присвоить значение -1, если площадь ∆АВС меньше или равна площади ∆PLF , и значение 1 – в противном случае. Для треугольника большей площади вычислить медианы и напечатать их в порядке возрастания. Вычисление площади треугольника оформить в виде подпрограммы.

Площадь треугольника со сторонами m, n, k может быть определена по формуле Герона , где r – полупериметр; медиана, проведенная к стороне m, равна .

---

5. Заданы стороны трех треугольников: а, b, c (∆АВС); p, l, f (∆PLF); m, n, k (∆MNK). Напечатать значения площадей в порядке возрастания. Вычисление площади произвольного треугольника представить в подпрограмме. Для треугольника со сторонами m, n, k площадь определяется формулой Герона ; где .

6. Составить подпрограмму вычисления площади треугольника по заданным двум сторонам а, b и углу между ними , используя формулу . Для заданных трех треугольников: ; ; определить, какой из них имеет наибольшую площадь.

7. Составить подпрограмму вычисления углов треугольника по заданным трем сторонам а, b, c, используя формулы, аналогичные следующим:

;

где — угол между сторонами а, b.

Для заданных двух треугольников: ; определить все углы и напечатать их в порядке возрастания.

8. Заданы четыре набора из трех чисел: ; ; ; . Для каждого набора чисел рассмотреть возможность построения треугольника, считая данные в наборе длинами сторон треугольника. Определение возможности построения треугольника по произвольным длинам сторон оформить в виде подпрограммы.

9. Составить подпрограмму вычисления площади S правильного n-угольника, вписанного в окружность радиуса R по формулам:

Для заданной окружности радиуса R определить площади вписанных в нее правильных треугольника, четырехугольника и пятиугольника.

10. Составить подпрограмму вычисления периметра P правильного n-угольника, вписанного в окружность радиуса R по формуле:

Для заданной окружности радиуса R определить ппериметры вписанных в нее правильных четырехугольника, пятиугольника и шестиугольника.

11. Заданы коэффициенты квадратных уравнений:

(коэффициенты a,b,c);

(коэффициенты d,f,r);

(коэффициенты p,q,k).

Найти минимальное значение среди корней этих уравнений. В случае комплексных корней принять за корни действительную и мнимую части. Решение квадратного уравнения оформить в виде подпрограммы.

12. Вычислить площадь выпуклого четырехугольника ABCD, заданного длинами своих сторон a,b,c,d и одной из диагоналей e: a — длина стороны AB; b — длина стороны BC; — длина стороны CD; d — длина стороны AD; e — длина диагонали AC. Вычисление площади четырехугольника в данном случае можно получить как сумму площадей двух треугольников. Вычисление площади произвольного треугольника представить в подпрограмме. Для треугольника со сторонами m, n, k площадь определяется формулой Герона ; где .

13. Четыре точки заданы своими координатами Определить и напечатать, сколько из них находится внутри круга с радиусом r, и одновременно – внутри квадрата со стороной а; r и а заданы. Проверку того, находится ли точка внутри круга и квадрата, оформить в виде подпрограммы.

14. Три точки заданы своими декартовыми координатами Вычислить и напечатать полярные координаты этих точек. Кроме этого, упорядочить и напечатать координаты точек по возрастанию полярного радиуса ρ. Полярный радиус ρ и полярный угол φ вычисляются по формулам . Перевод декартовых координат в полярные оформить в виде подпрограммы.

---