Добавлен: 31.01.2019
Просмотров: 332
Скачиваний: 7
1. Механические и электромеханические характеристики двигателей постоянного тока (ДНВ, ДПВ, ДСВ).
Механическая и электромеханическая характеристики.
Если рассматривать статику когда d/dt=0, тогда
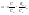 (2,5) – уравнение
электромеханической характеристики.
(2,5) – уравнение
электромеханической характеристики.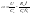 (2,6)
– уравнение механической характеристики.
(2,6)
– уравнение механической характеристики.
Т.к первый член U/Ce=ω0 (скорость идеального хх) постоянная величина, то обе характеристики механическая и электромеханическая будут представлять прямые линии и характеристики будут совпадать только по оси абсцисс будут разные масштабы.
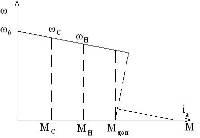 Мдоп=(2-3)Мн
Мдоп=(2-3)Мн
Iдоп=(2-3)Iн
Мкз=(15-20)Мн
Iкз=(15-20)Iн
Двигатель постоянного тока не в кое случае нельзя включать на номинальное напряжение без добавочного сопротивления.
Двигатели постоянного тока имеют допустимые значения которые нельзя превышать и указываются в паспортных данных.
Если характеристика получена при номинальном напряжении, номинальном потоке и отсутствии добавочного сопротивления то она называется естественной.
Если имеется добавочное сопротивление либо не номинальное напряжение, либо не номинальный поток, то характеристика называется искусственной.
Построение механической и электромеханической характеристик производится по 2 точкам.
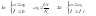
1т. В паспортных данных даются следующие значения: Рн, Uн, Iн, nн → ωн=πnн/30 (c-1)
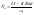
Внутреннее сопротивление якорной цепи можно определить следующими 3 способами.
1. По каталогу. Raд=(Rа+Rко+Rдп)кт+Rщ
2. Определяют по номограмме.
ρ=f(Рн)
 ,
,
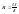
3. Если нет каталога, нет справочных данных, то пользуются эмпирической формулой.
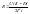
2т. Мн=СмIн=Мэм
1 - соединим 1 и 2 точки получим характеристику ω=f(Мэ)
3т.
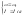
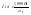
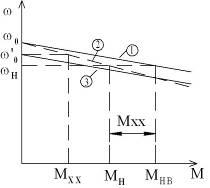
Однако 2 характеристика также не является механической характеристикой. Чтобы получить механическую характеристику откладываем от начала координат Мхх=Мн-Мнв. С Мхх поднимаем перпендикуляр до пересечения с 2. Эта точка определяет скорость идеального хх.
3 это и будет искомая механическая характеристика ω=f(Мнв).
2. Механические и электромеханические характеристики асинхронных двигателей.
Механические и токовые характеристики.
Для вывода механических и токовых характеристик рассмотрим схему замещения одной фазы.
![]()
Вынесем намагничивающий контур на зажимы.
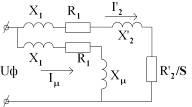
Как следует из схемы замещения ток в роторной цепи равен:
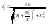 (3,1)
Хк=Х1+Х’2
(3,1)
Хк=Х1+Х’2
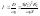
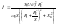 (3,2)
(3,2)
Взяв производную момента по S и приравняв к 0 получим:
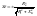 (3,3)
(3,3)
Подставим 3,3 в 3,2 получим.
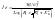 (3,4)
(3,4)
Разделив 3,2 на 3,4 получим при некоторых допущениях упрощенную формулу Клосса.
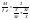
По формуле Клосса рассматривать влияние параметров неудобно поэтому рассматриваются формулы (3,2), (3,3), (3,4).
Рассмотрим вид механической характеристики или зависимости момента от скольжения используя формулу 3,2.

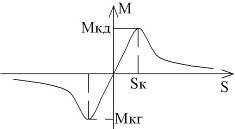
В формуле 3,4 «+» в двигательном режиме, «-» в генераторном режиме. Поэтому момент в генераторном режиме больше чем в двигательном в 2 и более раз.
Рассмотрим вид токовой характеристики в соответствии с выражением 3,1 при:
1. S=0, I’2=0
2.
При скольжении S=±∞,
ток
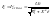
3.
При
S=1,
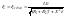
4. R1=R’2/2, S=- R’2/R1, I’2=Uф/Хк.
![]()
В электроприводе как правило механическую и токовую (эл мех) характеристики не в зависимости от скольжения, а в зависимости от скорости.
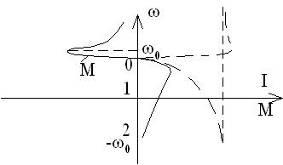
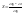 1. ω=ω0
S=0 2. ω=0 S=1 3. ω=-ω0
S=2 4. ω=2ω0
S=-1
1. ω=ω0
S=0 2. ω=0 S=1 3. ω=-ω0
S=2 4. ω=2ω0
S=-1
Намагничивающий ток составляет 20-30% от номинального,
I’2n=(4-7)Iн, 4 - для маломощных, 7 – для двигателей большой мощности.
3. Тормозные характеристики двигателей постоянного тока.
Тормозные режимы работы привода.
Для данного типа привода существует 3 основных тормозных режима:
1. Динамическое торможение. 2. Торможения противовключения. 3. Рекуперативное торможение.
Реализация того или другого вида тормозного режима определяется не только схемой включения электродвигателя, но и характером нагрузки на его валу (реактивная или активная). Кроме этого тормозные режимы могут реализовываться только в динамических процессах для некоторых электроприводов и не реализовываться в статических режимах.
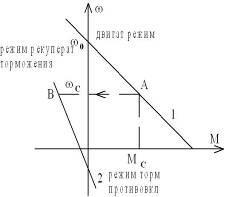
Двигательный режим.
0<Мс<Мкз, момент статический направлен встречно моменту двигателя.
0<ω<ω0
Режим динамического торможения.
Это такой режим когда механическая энергия превращается в электрическую и реализуется в замкнутом контуре изолированном от сети. Динамическое торможение может быть в двух случаях:
1. с самовозбуждением
2. с независимым возбуждением.
Если и якорную цепь и обмотку возбуждения отключить от сети и замыкаем на тормозное сопротивление, то до определенных скоростей возникает режим динамического торможения с самовозбуждением.
1. Данный режим реализуется с любым по характеру моментом на валу двигателя.
2. Этот режим протекает без потребления энергии из электрической сети.
3. Менее эффективен по тормозным качествам, чем предыдущие.
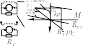
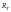

Характеристики динамического торможения имеют неблагоприятный вид т.к. торможение будет около скоростей ωКР находящихся около ω0/2. Меняя тормозное сопротивление можно тормозную характеристику получить ниже. Используется т/о в аварийном режиме. Если якорную цепь замкнуть на тормозное сопротивление Rт, а обмотку возбуждения поставить подключенной к питающей сети, то двигатель переходит в работу в динамическом торможении с независимым возбуждением, который проходит через начало координат. Меняя тормозное сопротивление Rт (RТ2 < RТ1) можно менять скорость тормозного спуска в 4ом квадранте.
Режим торможения противовключения.
Это такое торможение когда под действием запасенной эл. энергии двигатель вращается в сторону противоположную направлению момента развиваемого двигателем. Торможение противовключением встречается в двух случаях: при спуске тяжелого груза и при реверсе.
Мс>Мкз
Мс должен быть активный по характеру, в этом случае вращение вала двигателя осуществляется под воздействием момента создаваемого нагрузкой.
Мд>0 ω<0
Двигатель создает тормозной момент уравновешивая в статическом режиме момент нагрузки. Данный режим реализуется с потреблением электрической энергии из сети.
Режим рекуперативного торможения.
Это такой режим, когда под действием потенциальных сил двигатель вращается со скоростью выше скорости идеального хх.
Возможен в статическом режиме при условии активного характера нагрузки, если момент нагрузки по направлению совпадает с направлением момента двигателя. При превышении частоты вращения значения ω0, момент двигателя меняет свой знак становясь тормозным, а привод переходит в режим рекуперации.
М<0, ω>0. Электрическая энергия из сети не потребляется. Двигатель начинает работать генератором с отдачей энергии в сеть. Направление тока якоря меняется по отношению к двигательному режиму. Для обеспечения этого режима на практике необходимо использовать специальные электронные устройства-инверторы, преобразующие постоянный электрический ток в переменный однофазный или 3-х фазный.
В системах генератор-двигатель режим рекуперативного торможения реализуется автоматически. Генератор питающий двигатель, начинает работать двигателем, а синхронная машина, приводящая в движение генератор начинает работать генератором переменного тока.
4. Тормозные режимы двигателей последовательного возбуждения. Возможность работы на холостом ходу.
Тормозные режимы.
Двигатель последовательного возбуждения или сериестный двигатель имеют только 2 тормозных режима: режим динамического торможения и режим противовключения. Т.к. двигатель последовательного возбуждения не может работать на холостом ходу значит он не может работать в режиме рекуперативного включения.
Динамическое торможение.
Динамическое торможение может быть в 2 случаях либо с самовозбуждением, либо с независимым возбуждением.
Динамическое торможение с самовозбуждением.
![]()
Если отключить якорную цепь от сети и подключить на тормозное сопротивление, то начинается режим динамического торможения с самовозбуждением.
Для того чтобы возник режим самовозбуждения необходимо при этом изменить полярность цепи обмотки возбуждения. Тем не менее вид характеристики имеет не благоприятный вид, т.к торможение идет до определенной критической скорости. Меняя тормозное сопротивление можно уменьшить критическую скорость.
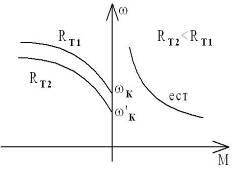
Динамическое торможение с независимым самовозбуждением.
![]()
Если якорную цепь замкнуть на тормозное сопротивление, а обмотку возбуждения подключить к сети ч/з добавочное сопротивлении, так чтобы по ней протекал ток возбуждения номинальный, то начинается режим динамического торможения с независимым возбуждением, когда характеристика проходит ч/з 0 и не отличается от характеристики динамического торможения шунтового двигателя. Только потери для двигателя последовательного возбуждения в 10 раз выше, чем для шунтового двигателя и равны номинальным потерям.
Торможение противовключением.
Торможение противовключением возможно в 2 случаях: при спуске груза, при реверсе.
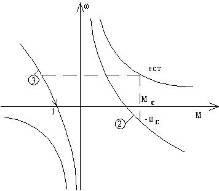
При велении большого добавочного сопротивления двигатель будет работать со скоростью ω0, работая в режиме противоключения. При реверсе двигатель переходит с естественной характеристик на характеристику 3, происходит эффект торможения в т 1 двигатель отключается.
5. Основные понятия электропривода. Классификация электроприводов.
Классификация электроприводов.
Электропривода могут быть классифицированы по следующим признакам:
1. По виду движения:
- ЭП вращательного однонаправленного и реверсивного движения.
- ЭП поступательного однонаправленного и реверсивного двияжения.
- ЭП поступательно-вращательного движения.
2. По характеру движения:
- ЭП непрерывного движения. - ЭП пульсирующего движения.
3. По скоростному виду.
ЭП с постоянной скоростью;ЭП с эпизодически меняющейся скоростью;ЭПс изменяющейся по определенному закону скорости.
4. По характеру передачи энергии от двигателя к рабочей машине.
- групповой привод. - однодвигательный ЭП или индивидуальный. - многодвигательный.
Групповой ЭП это такая система, когда один двигатель приводит в движение группу исполнительных механизмов.
![]()
Недостатки:
1. Громоздкость трансмиссии. 2. Большие площади. 3. Невозможность автономной работы.
Однодвигательный привод – когда каждый исполнительный механизм приводится приводится отдельными электродвигателями.
![]()
Достоинства:
1. Увеличивается надежность передач, упрощаются трансмиссии. 2. Возможна автономная работа каждого исполнительного механизма. 3. Возможность широкой автоматизации.
Многодвигательный привод – это такая система когда каждый рабочий орган рабочей машины приводится в движение отдельным двигателем.
Если например в металлорежущих станках используется один двигатель, то это индивидуальный ЭП, а если на вращение детали на продольном и поперечном движении резца используются разные двигатели, то это многодвигательный привод.
Определение электропривода.
Электроприводом называется электромеханическое устройство, преобразующее электрическую энергию в механическую и обеспечивающее электроуправление механической энергией.
ЭП состоит из 3-х частей:
- электрического двигателя;
- механической части при помощи которой движение передается от двигателя к исполнительному механизму;
- системы управления.
Структурно ЭП можно представить следующим образом:
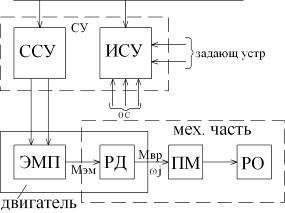
ССУ – силовая часть системы управления – представляет преобразователь который может быть различен в зависимости от типа двигателя. Для двигателя постоянного тока преобразователь преобразует переменное напряжение сети в регулируемое постоянное напряжение. Для двигателя переменного тока преобразователь преобразует переменное напряжение сети неизменной частоты в переменное напряжение регулируемой частоты.
ЭМП – электромеханический преобразователь.
РД – ротор двигателя – преобразует электромагнитный момент во вращающий момент на валу.
РД входит как в двигатель, так и в механическую часть
ПМ – передаточный механизм или редуктор.
ИСУ – информационная часть системы управления – включает в себя аппаратуру управления, реле, пускатели, контакторы и т.д. Нелинейные блоки (блоки перемножения), функциональные блоки и т.д. Блоки защиты, блок датчиков и блок задающих устройств. РО – рабочий орган.
На основании сравнения текущего состояния системы с датчиков обратной связи и заданных сигналов с блоков заданных устройств, информационная часть СУ формирует задание на силовую часть СУ или преобразователь.
ЭП могут быть стационарными и автономными.
6. Приведение моментов инерции, жесткостей, моментов сопротивления.
1. Приведение моментов инерции.
Основой приведения моментов инерции является равенство кинематических энергий приведенного и реального элементов кинематической схемы.
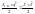 ,
,
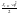 - кинетическая энергия приведенного
элемента,
- кинетическая энергия приведенного
элемента,
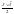 - кинетическая энергия реального
элемента.
- кинетическая энергия реального
элемента.
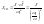 ,
,
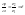 - передаточное число.
- передаточное число.
где z1 – число зубьев ведомой шестерни.
z2 – число зубьев ведущей шестерни.
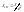 при приведении
вращательного движения к вращательному
движению вала двигателя.
при приведении
вращательного движения к вращательному
движению вала двигателя.
При приведении поступательного движения к вращательному.
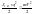 .
.
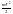 -
кинетическая энергия реального элемента.
m
– масса реального элемента. V
– линейная скорость реального элемента.
-
кинетическая энергия реального элемента.
m
– масса реального элемента. V
– линейная скорость реального элемента.
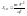 .
.
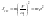 - приведение поступательного движения
к вращательному.
- приведение поступательного движения
к вращательному.
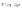 - радиус приведения.
- радиус приведения.
2. Приведение жесткостей.
Основой приведения жесткостей является равенство потенциальных энергий приведенного и реального элементов кинематической цепи.
Потенциальная
энергия связана с понятием жесткости.
При вращательном движении жесткость
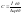 - это отношение крутящего момента к
деформации угла.
- это отношение крутящего момента к
деформации угла.
При поступательном движении.
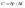
Потенциальная энергия приведенного элемента
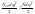 ,
,
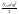 - потенциальная энергия приведенного
элемента,
- потенциальная энергия приведенного
элемента,
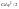 -
потенциальная энергия реального
элемента.
-
потенциальная энергия реального
элемента.
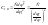 .
.
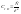 приведение вращательного движения к
вращательному.
приведение вращательного движения к
вращательному.
При приведении поступательного движения к вращательному приравниваем поступательные энергии реального элемента и приведенного.
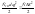 ,
,
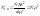
3. Приведение моментов сопротивлений.
Основой приведения моментов сопротивлений является равенство элементарных работ для реального и приведенного элементов кинематической цепи.
Приравняем элементарные работы реального и приведенного.
Мпрdφ1= МCdφ
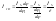 - приведение
вращательного движения к вращательному.
- приведение
вращательного движения к вращательному.
При приведении линейного движения к вращательному приравниваем элементарные работы приведенного и реального элементов.
Мпрdφ1=
FdS
,
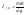 ,
Мпр=
Fρ
,
Мпр=
Fρ
7. Уравнение движения.
Уравнение движения рассматриваем для 2-х массовой механической системы.
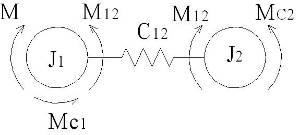
Воспользуемся для вывода уравнения движения уравнением Лагранж второго рода.
 ,
,
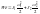
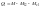 ,
,
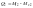
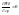
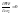 ,
,
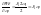 ,
,
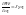
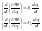 Т.о.
Т.о.
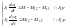
Для того чтобы математическое описание механической части электропривода было полным необходимо знать закон изменения упругого взаимодействия.
 ,
,
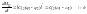
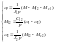 В
соответствии с этой системой уравнений
составим структурную схему механической
части.
В
соответствии с этой системой уравнений
составим структурную схему механической
части.
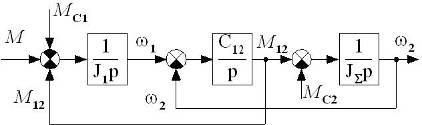
Получили структурную схему механической части 2-х массовой системы без учета вязкого трения. Такая структурная схема иногда используется для синтеза системы управления.
Рассмотрим поведение упругого момента.
М12=Му
 ,
,
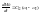 ,
,
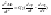
Допущения: пренебрегаем МС1 и МС2.
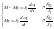
Умножим
обе части первого уравнения на
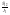 ,
а второго на
,
а второго на
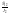 и вычтем из первого второе.
и вычтем из первого второе.
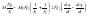 ,
,
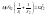
Ω12 – это частота собственных колебаний системы.
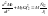
Момент упругий будет изменяться по колебательной не затухающей зависимости.
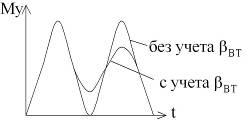
Любая механическая система содержит вязкое трение поэтому упругий момент можно выразить следующим образом.
 ,
,
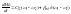
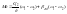 ,
,
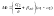
С учетом вязкого трения Му будет представлять затухающие колебания, причем чем меньше жесткость, тем меньше колебаний. Жесткость выбирается опытным путем в зависимости от кинематики и может составлять от одной сотой С12 до 0,1 С12 при наличии в кинематики канатов.
Структурная схема с учетом вязкого трения может быть представлена в следующем виде.
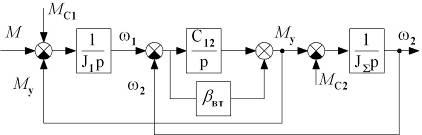
Данная структурная схема применяется для большинства механизмов.
8. Структура механической части электропривода с учетом климатических погрешностей и зазоров.
Для
того что бы учесть кинематические
погрешности их учитывают коэффициентом
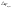 .
Зазоры учитывают при помощи нелинейного
звена следующего вида:
.
Зазоры учитывают при помощи нелинейного
звена следующего вида:
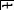
Как привило при работе зазор увеличивается, допустимый износ до 40%.
С учетом зазоров и кинематических погрешностей которые можно представить аналитически в следующем виде:
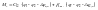 ;
;
Если
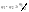 ,
то увеличивается.
,
то увеличивается.
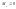 если
если
 .
.
Структурная схема:
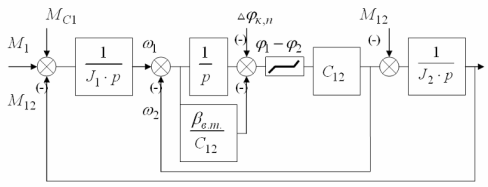 9.
Тормозные режимы асинхронных двигателей.
9.
Тормозные режимы асинхронных двигателей.
Тормозные режимы.
Асинхронный двигатель работает в следующих тормозных режимах.
1. Рекуперативное торможение.
2. Торможение противовключеия.
3. Динамическое торможение.
4 Конденсаторное торможение.
5. Возможно сочетание режимов.
Рекуперативное торможение.
Рекуперативное торможение это такой вид торможения когда под действием потенциальных сил двигатель вращается со скоростью выше скорости реального хх, потребляет из сети реактивную энергию и выделяет в сеть активную.
Рекуперативное торможение встречается в 3-х случаях при спуске груза, при переключении числа пар полюсов (переключение со звезды на треугольник), при резком уменьшении частоты.
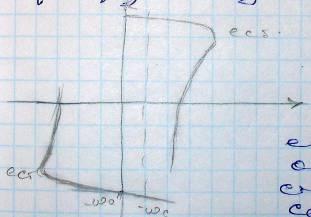
При включении двигателя на спуск двигатель разгоняется по характеристики в 3 квадранте. Скорость его под действием опускающего груза становиться выше скорости ω0. Двигатель переходит в 4 квадрант и затем начинает устойчиво работать со скоростью ωС, в режиме рекуперативного торможения отдавая активную энергию в сеть.
Торможение противовключением
Используется в 2-х случаях: 1) при реверсе ; 2) при спуске тяжелого груза
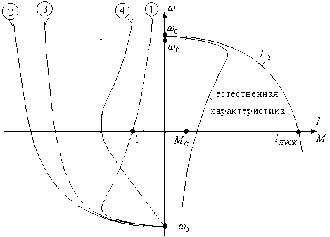 рис1
рис1
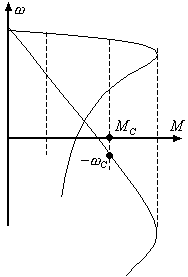 рис2
рис2
По рис 1: При перемене двух линейных проводов статорной цепи двигатель переходит с естественной механической или токовой характеристики на характеристики (1) и (2) соответственно. Происходит резкое торможение и в точке 1 необходимо отключить двигатель. Т.к. токи при реверсе будут больше, чем при пуске, то их нужно ограничивать. Если это АД с фазным ротором, то вводят большое добавочное сопротивление в роторную цепь, тогда токовая характеристика будет в виде (3), а мех. – (4). При этом токи уменьшаются и, как результат, эффективность торможения увеличивается.
По рис 2: При введении большого добавочного сопротивления в роторную цепь.
Динамическое торможение
Если статор асинхронного двигателя отключить от сети и подать в обмотки статора постоянный ток:

Двигатель переходит в режим динамического торможения.
По обмоткам статора протекает постоянный ток, создавая неподвижное магнитное поле. Ротор двигателя продолжает вращаться, и обмотки ротора пересекают неподвижное магнитное поле статора. В результате в них наводится ЭДС, а по обмоткам ротора начинает протекать ток. При взаимодействии тока ротора с неподвижным магнитным полем статора возникает тормозной момент. В отличии от двигательного режима, ток статора является постоянным, а намагничивающий ток зависит от скольжения.
По форме механическая характеристика в режиме динамического торможения похожа на мех. хар-ку в двигательном режиме (момент так же начинает увеличиваться, достигает максимума и затем стремится к нулю), только в двигательном режиме хар-ка начинается с ω0, а в режиме динамического торможения – с нуля.
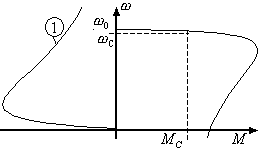
Если двигатель работал на естественной характеристике и внезапно подали постоянное напряжение в обмотку статора, двигатель переходит на (1), при чем при уменьшении скорости тормозные моменты увеличиваются и достигают максимума, затем двигатель тормозится до нуля.
В режиме противовключения эффективность торможения выше, однако, при ω=0 при противовключении нужно отключать двигатель, а при динамическом торможении такой необходимости нет.
Конденсаторное торможение
 Если
статорную цепь АД отключить от сети
переменного тока и замкнуть на
конденсаторную батарею, а обмотку
ротора замкнуть накоротко, то двигатель
переходит работать в режим самовозбужденного
конденсаторного торможения.
Если
статорную цепь АД отключить от сети
переменного тока и замкнуть на
конденсаторную батарею, а обмотку
ротора замкнуть накоротко, то двигатель
переходит работать в режим самовозбужденного
конденсаторного торможения.
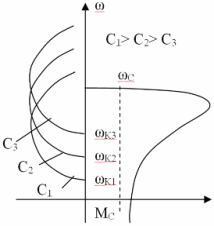
Режим самовозбуждения возникает только до критических скоростей, величина которых от 1/3ω0 до 1/2ω0, в зависимости от величины конденсаторов.
Эффективность торможения можно увеличить за счет применения комбинированного торможения конденсаторного с короткозамыканием.
10. Электромагнитные переходные процессы при различных схемах включения.
Обмотку возбуждения генератора можно подключать либо к сети постоянного тока, либо к статическим или вращающимся возбудителям – источники постоянного тока для питания обмотки возбуждения.
Рассмотрим несколько принципиальных схем включения ОВ генератора. Рассмотрим схемы питания от источника постоянного тока.
Нормальная схема
Предполагает включение обмотки возбуждения на номинальное напряжение.
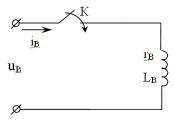
При включении рубильника ток возбуждения не может достигнуть мгновенно установившегося значения равного номинальному току возбуждения, т.к. существует ЭДС самоиндукции.
Баланс напряжения.
 ,
,
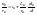
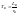 -
электромагнитная постоянная возбуждения.
-
электромагнитная постоянная возбуждения.
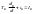 (5,1) дифференциальное
уравнение 1-го порядка с правой частью
имеет решение
(5,1) дифференциальное
уравнение 1-го порядка с правой частью
имеет решение
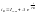
А
– постоянная интегрирования находимая
из начальных условий при
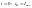 .
.
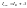 ,
,
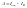 ,
,
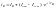 (5.2)
(5.2)
Если
Iнач=0,
то
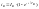 (5.3)
(5.3)
Как следует из выражения (5.3) переходный процесс представляет экспоненту.
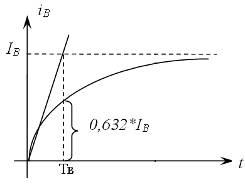
Теоретически время переходного процесса = ∞, практически же время переходного процесса = 3Тв через это время ток достигнет 95% от установившегося значения.
Геометрический
смысл:
 -
это время, в течение которого ток
достигает 0,632 от установившегося
значения.
-
это время, в течение которого ток
достигает 0,632 от установившегося
значения.
Физический смысл: Тв - это время в течении которого ток достиг бы установившегося значения, если бы не было потерь на нагрев.
Тв=0,2с до нескольких минут для больших двигателей, т.е. время переходного процесса стараются использовать схемные решения позволяющие уменьшить время переходного процесса.
Схема с добавочным сопротивлением.
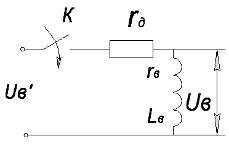
Предполагаем
что схема включается на повышенное
напряжение
 .
.
В схеме с добавочным сопротивлением Rд выбирается таким образом, что
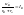 .
Отношение
.
Отношение
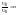 называется коэффициентом форсировки
и определяется добавочным сопротивлением.
называется коэффициентом форсировки
и определяется добавочным сопротивлением.
Закон изменения тока возбуждения в схеме с добавочным сопротивлением будет иметь вид.
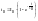 (5.4)
(5.4)
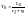 ,
т.е.
,
т.е.

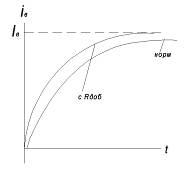
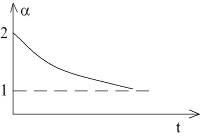
Т.к. коэффициент форсировки не остается постоянным, а меняется по экспоненте. В результате этого процесс идет форсировано на начальном этапе, а затем с rД. Поэтому время переходного процесса с rД уменьшается, но не пропорционально коэффициенту форсировки, т.е. время уменьшается не значительно по сравнению с нормальной схемой. Поэтому схема с добавочным сопротивлением используется только для маломощных генераторов и для питания катушек, контакторов с использованием коэффициента форсировки равного примерно 2.
Схема с форсировочным сопротивлением.
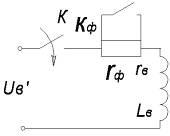
Схема
предполагает наличие повышенного
напряжения
 ,
коэффициент форсировки
,
коэффициент форсировки
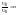 может
меняться в широких пределах. Сопротивление
форсировки на время пуска шунтируется
замыкающим контактом Кф
форсировочного контактора.
может
меняться в широких пределах. Сопротивление
форсировки на время пуска шунтируется
замыкающим контактом Кф
форсировочного контактора.
На время пуска повышенное напряжение прикладывается к обмотке возбуждения, приводит к тому что начинается форсировачный рост тока возбуждения по закону.
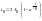 (5.5)
(5.5)
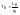 - такое же как в
нормальной схеме.
- такое же как в
нормальной схеме.
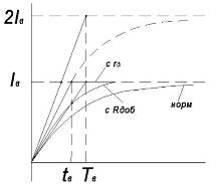
Т.о. после достижения током установившегося значения в т. а, что достигается за время tВ. В это время вводится сопротивление форсировачное и рост тока возбуждения прекращается, т.о. время переходного процесса получается меньше чем Тв.
чем больше коэффициент форсировки, тем меньше время переходногопроцесса.
Существует рациональная граница изменения коэффициента форсировки.
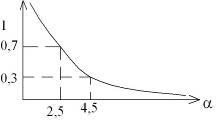
При коэффициенте α=2,5 отношение tB/Tв=0,7, при α=4,5 отношение tB/Tв=0,3.
Дальнейшее уменьшение α до 0 ведет к увеличению до ∞ отношения, а увеличение α к ∞ влечет за собой уменьшение времени переходного процесса.
Граница рационального изменения α является граница от 2,5 до 4,5. В принципе на практике можно использовать увеличение питающего напряжения в 10 раз, т.е. коэффициент форсировки α может быть =10. Дальнейшее увеличение чревато пробоем изоляции.
Кроме рассмотренных схем используются схемы со статическими или вращающимися возбудителями.
К статическим возбудителям относятся силовые магнитные возбудители которые до сих пор используются на некоторых объектах горной промышленности, более современные тиристорные возбудители.
Некоторые вращающиеся возбудители имеют быстродйествие большее, чем у магнитных возбудителей.
Наиболее употребительными являются следующие схемы с вращающимся возбудителем:
1. Схема профессора Морозова, которая имеет переходные процессы близкие к схеме с rД, но форсировка автоматически включается и выключается.
2. Схема с противо компаундным возбудителем.
3. Схема с электродинамической емкостью.
11. Электромеханические переходные процессы при пуске в системе Г-Д. Пуск.
Для питания ОВГ используется схема с форсировочным сопротивлением.
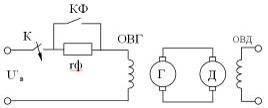
ЭДС генератора будет изменяться так же как ток возбуждения.
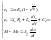 (5.6)
(5.6)
Пренебрегая вторым членом приравниваем правые части 1 и 2 уравнения и проведя ряд преобразований получим закон изменения скорости.
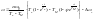 (5.7)
(5.7)
Из выражения (5,7) скорость состоит из 2-х экспонент, постоянные времени которых существенно отличаются
Тв>>Тм
,
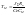
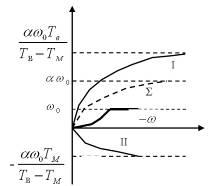
Для того чтобы представить характер изменения тока якорной цепи из 3-го уравнения (5.6) получим:
М=См∙iа.
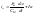
Возьмем производную от выражения (5.7)
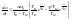 ,
,
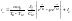
Сомножитель перед дробью представим в виде
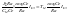 ,
,
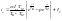 (5.8)
(5.8)
Ток ЯЦ определяется разностью значений ЭДС генератора и ЭДС двигателя, т.е.
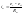
Поэтому качественный характер изменения тока ЯЦ.
Нарисуем и покажем изменение ЭДС генератора и ЭДС двигателя и IЯЦ.
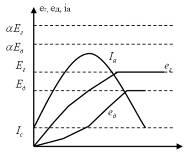 Т.о.
ток достигает максимального значения,
который можно определить, взяв производную
от (5,8) и приравняв к 0 найдем время
достижения максимума и подставив в
(5,8), найдем максимальное значение тока.
Подставив в место Imax
Iдоп
найдем необходимый коэффициент
форсирования.
Т.о.
ток достигает максимального значения,
который можно определить, взяв производную
от (5,8) и приравняв к 0 найдем время
достижения максимума и подставив в
(5,8), найдем максимальное значение тока.
Подставив в место Imax
Iдоп
найдем необходимый коэффициент
форсирования.
12. Электромеханические переходные процессы при торможении в системе Г-Д.
Торможение
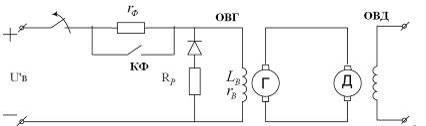
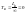
Если рубильник отключить от сети, то возникает большой бросок перенапряжения, в результате наступит пробой изоляции. Для этого ставим разрядное сопротивление, а чтобы оно не мешало при пуске, ставим диод.
При размыкании рубильника ЭДС начинает падать через RР.
 ,
тогда
,
тогда
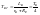 т.е.
при торможении время электромагнитного
переходного процесса примерно в 4 раза
быстрее, чем при пуске. Ток возбуждения
спадает по экспоненте.
т.е.
при торможении время электромагнитного
переходного процесса примерно в 4 раза
быстрее, чем при пуске. Ток возбуждения
спадает по экспоненте.
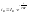 .
По такому же закону изменяется ЭДС
генератора.
.
По такому же закону изменяется ЭДС
генератора.
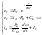 (5.9)
(5.9)
Приравняем правые части системы (5,9). После преобразования получим закон изменения скорости.
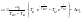 (5.10)
(5.10)
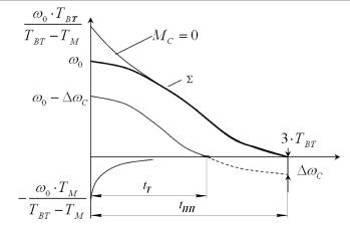
Как следует из (5.10) скорость состоит из двух спадающих экспонент, определяемых постоянной времени, причем ТВТ>>TM.
13. Электромеханические переходные процессы при реверсе в системе Г-Д.
Реверс
Чтобы получить реверс нужно осуществить изменение полярности в цепи возбуждения двигателя.
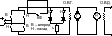
Реверс
можно осуществить либо за счет контактного
реверсора, либо за счет бесконтактного.
Пока размыкаются контакторы на момент
размыкания (срабатывания контакторов)
в цепь О.В.Г. вводится разрядное
сопротивление. Пока срабатывает
контактная аппаратура, ЭДС генератора
спадает и идет процесс торможения
рассмотренный выше. За это время
 спадает до величины
спадает до величины
 .
.
Динамика или мат описание динамического процесса будет описываться следующей системой
Переходный процесс будет описываться
ЭДС генератора спадает при изменении полярности.
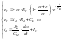
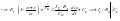 ,
,
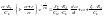
Упростим выражение.
Таким образом мат описание ПП система ГД при реверсе сводится к одному дифференциальному уравнению 1-го порядка
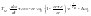 ;
;
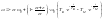
Чтобы определить значения или закон изменения тока
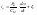
Найдём производную по скорости:
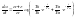 ,
,
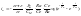 ,
,
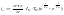
Рассмотрим
переходный процесс на плоскости фазовых
координат в координатах
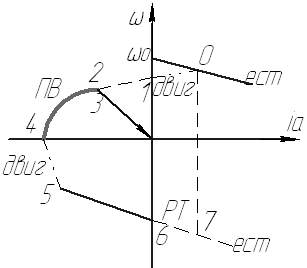
Эта картина представит характер переходных процессов, на которых будет показано, что на различных участках двигатель работает не только в режиме рекуперативного торможения, но и в режиме противовключения и двигательном режимах.
14. Электромеханические свойства системы генератор-двигатель.
Для получения специальных характеристик используют системы генератор – двигатель эта система может быть на машинах последовательного возбуждения или на машинах независимого возбуждения наиболее часто применяется на машинах независимого возбуждения, в качестве возбудителя могут применяться либо вращающийся преобразователь либо статические тиристорные.
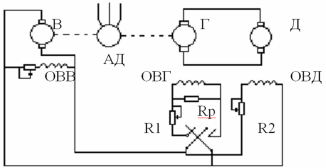
То есть на одном валу находится асинхронный двигатель, возбудитель, генератор питающий якорную цепь двигателя. С начала запитывается асинхр двигатель причем сопротивление R1 полностью введено, а сопротивление R2 полностью выведено то есть поток двигателя номинальный. Изменяя сопротивление R1 увеличиваем поток возбуждения генератора, появляется напряжение на зажимах генератора, двигатель разгоняется.
Т.к. сопротивление якорной цепи включает в себя внутреннее сопротивление цепи двигателя и генератора то характеристика в системе ГД мягче чем при питании от источника постоянного тока .
Регулирование характеристики в системе ГД га счет изменения потока генерат., или потока возбуждения
Изменяя поток возбуждения получаем характеристики Которые параллельны естественной.
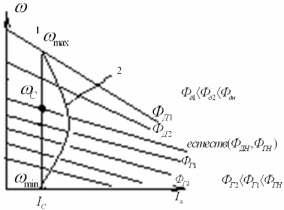
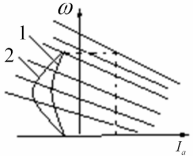
Если плавно менять с начала поток двигатель, а потом поток генератор, то двигатель плавно переходит с одной характиристики на другую осуществляется режим рекуперативного торможения, торможение до нуля с отдачей энергии в сеть. Если темп изменения потока будет выше, то торможение будет происходить по характеристике 2.
15. Электромеханические переходные процессы в асинхронных двигателях.
Электромеханические ПП в АД.
Общепринято вид механической характеристики построенной по формуле Клосса.
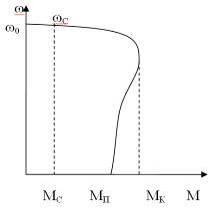
Фактически характеристика может иметь вид, совершенно отличающийся от указанного.
Для того чтобы построить ПП нужно учесть и электромагнитные и механические ПП. Считаем что двигатель симметричный, то есть симметричное питание обмоток статора, идентичные сопротивления в фазах статора и ротора, идентичные индуктивности в фазах статора и ротора. И идентичные взаимо индуктивности между обмотками статора и ротором.
Тогда расположение мгновенных значение напряжений в фазах статора и ротора будут согласно диаграмме.
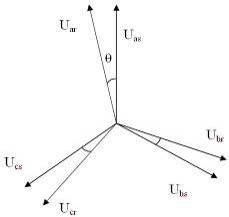
Uаs , Ubs , Ucs – мгновенные значения напряжений в фазах статора. Uаr, Ubr, Ucr – мгновенные значения напряжений в фазах ротора.
Система уравнений для напряжений в фазах статора и ротора соответственно будет иметь вид:
 (5,11) для статора.
(5,11) для статора.
 (5,12) для ротора.
(5,12) для ротора.
 ;
;
 ;
;
 - потокосцепление в фазах статора.
- потокосцепление в фазах статора.
 ;
;
 ;
;
 - потокосцепление в фазах ротора. Каждое
потоко сцепление является функцией
всех токов фаз статора и ротора.
- потокосцепление в фазах ротора. Каждое
потоко сцепление является функцией
всех токов фаз статора и ротора.
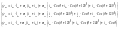 (5,13)
(5,13)
Потокосцепления в фазах ротора по аналогии можно записать следующей системой уравнений:
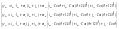 (5.14)
(5.14)
Таким образом получим 12 уравнений с 12-ю неизвестными. Которые дополним следующими тремя уравнениями:
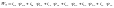 (5,15)
(5,15)
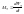 (5.16)
(5.16)
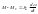 (5.17)
(5.17)
Т.о. получим 15 уравнений и если бы не учитывать нелинейность и насыщение, то определить ПП было бы крайне сложно. Поэтому практически исследовать ПП, особенно несколько десятилетий назад было невозможно.
Вводят пространственные комплексы: U, I и ψ. В результате системы уравнений (5.11), (5.12), (5.13) (5.14) сокращаются в три раза.
Пространственные комплексы тока статора и тока ротора после соответствующих решений состоят из 3-х составляющих установившихся значений и двух периодичных значений.
Поэтому момент который равен
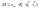
произведению пространственных комплексов тока статора и тока ротора (сопряженные) будет состоять из 6 составляющих: одной установившейся, двух апериодических и трех периодических.
Поэтому динамическая характеристика при пуске будет существенно отличаться от ………………..

Т.о. при пуске броски могут превышать в 2 и более раз момент критический, причем колебания будут в начальный момент и в конечный.
Кроме пускового опасным является режим запуска не остановившегося двигателя, что широко применяется при наладке приводов.
Режим переключения со звезды на треугольник. Самым опасным режимом является режим торможения противовключения.
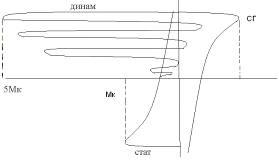
Т.о. при включении торможения противовключения бросок момента может достигать 4-5 кратных значений Мкр или же 15-20 раз > чем Мном.
Чтобы избежать этого можно на момент пуска или торможения вводить в статорную цепь добавочные желательно активные сопротивления.
16. Теория нагрева электрических двигателей.
Допущения:
1.Считаем, что все части машины нагреваются одинаково.
2.Теплопередача пропорциональна нагреву.
Словесно уравнение теплового баланса можно представить в следующем виде:
![]()

 Aτdt
Aτdt
 - основное уравнение
теплового баланса.
- основное уравнение
теплового баланса.
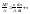
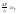
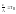
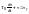
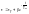
β-постоянная интегрирования.
Начальные
условия:
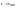 при t
= 0 Уравнение нагрева:
при t
= 0 Уравнение нагрева:
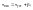
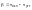
Вместо
β подставляем, получим:
 (4.1)
(4.1)
Рассмотрим частные случаи:
а) Пуск:

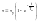
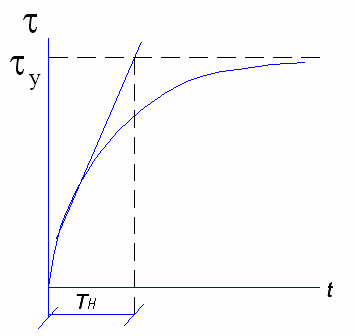
б)Торможение
:

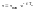 Будет спадающая экспонента:
Будет спадающая экспонента:
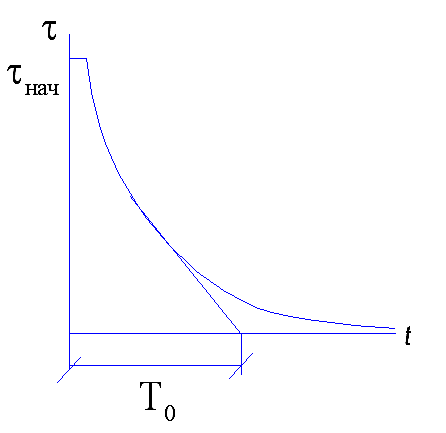
Постоянные
времени нагрева и охлаждения имеют
разные величины, а именно при охлаждении
постоянная времени больше. Могут быть
еще режимы наброса и сброса нагрузки.
При набросе нагрузки происходит
нагревание машины от
 до
до
 его экспоненте по формуле 4.1.
его экспоненте по формуле 4.1.
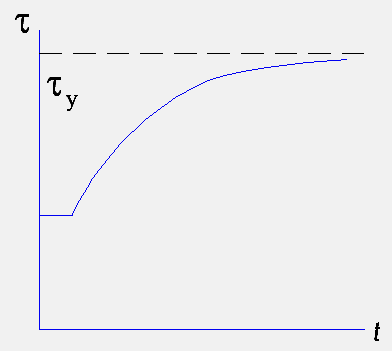
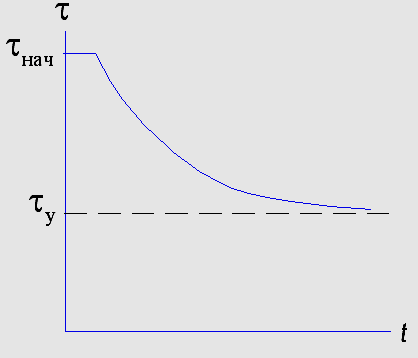
Наброс нагрузки Сброс нагрузки
В
результате работы разных двигателей
получаются разные условия нагревания
и охлаждения, которые учитываются
коэффициентом
 неоднородности охлаждения и нагревания.
неоднородности охлаждения и нагревания.
 принимает значения
принимает значения
 =0,85-0,95
для машин с независимой вентиляцией и
=0,85-0,95
для машин с независимой вентиляцией и
 =0,25-0,45
для машин с самовентиляцией. Постоянная
времени нагрева:
=0,25-0,45
для машин с самовентиляцией. Постоянная
времени нагрева: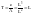
Чем больше габариты машины (мощность двигателя), тем больше постоянная времени нагрева. (от нескольких минут до нескольких часов).
17. Номинальные режимы.
При работе двигателей возможна работа в различных пусковых, тормозных, пуско-тормозных и реверсивных режимах. Причем необходимо было бы проектировать большое количество двигателей. Практически в электромашиностроении проектируют только 3 типа двигателей: двигатели длительного (продолжительного режима), двигатели кратковременного режима и двигатели повторно-кратковременного режима. Причем по конструкции они существенно отличаются.
ГОСТом предусмотрено 8 номинальных режимов: S1,S2,S3,S4,S5,S6,S7,S8.
Номинальные режимы это такие режимы, для которых заводом изготовителем гарантируется полное использование в тепловом отношении.
Заводом изготовителем изготавливают двигатели на следующие параметры: Рн Вт, кВт ; Uн В, кВ; Iн А, кА; nн об/мин; ωн=πn/30 рад/с, с-1; ηн ;cos(φн).
Рассмотрим первые 3 режима.
Режим S1 – называется продолжительным, это такой режим когда нагрузка приложена длительное время в течение которого двигатель успевает нагреться до установившейся температуры.
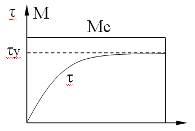
Режим
S2
– кратковременный режим – это такой
режим, когда в время работы значительно
меньше времени паузы. Причем за время
работы двигатель не успевает нагреться
до установившейся температуры, а за
время паузы успевает остыть до температуры
окружающей среды;

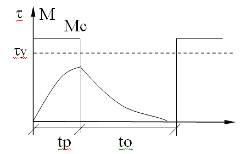
Режим S3 – повторно-кратковременный режим, это такой режим, когда чередуется времена работы и времена пауз. Когда за время работы двигатель не успевает нагреться до установившейся температуры, а за время паузы не успевает остыть до температуры окружающей среды.
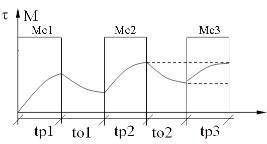
При выполнении нескольких циклов достигается законченный тепловой процесс.
Характерной величиной повторно-кратковременного режима является
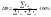
ГОСТом предусмотрены значения.
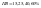
Другой характерной величиной число циклов в час Z.
Время цикла
Tц =3600/Z.
Z может иметь следующие значения Z=30,60,90,120,200,240,300.
Другой
величиной характеризующей
повторно-кратковременный режим является
величина
 - коэффициент инерционности.
- коэффициент инерционности.
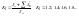
Если коэффициент инерционности превышает значение 2, то необходимо искать ошибку в вычислении моментов инерции элементов кинематической схемы. Для некоторых механизмов есть отступление от этого правила, в частности поворотные механизмы могут иметь коэффициент инерционности = 15,20 и более.
Рассмотренные три типа двигателей используются для изготовления серийных двигателей. Остальные номинальные режимы базируются на серии S1 и S3.
Режим S4 - это такой повторно-кратковременный режим в котором пуска соизмеримо с временем работы
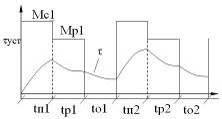
Режим S5 – такой повторно-кратковременный режим в котором на нагрев оказывает влияние и время пуска и время торможения.
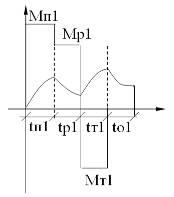
Режим S6 - это такой продолжительный режим чередования рабочих режимов и ХХ. При котором время переходных процессов не учитывается.
Характерной величиной является продолжительность нагрузки.
ГОСТом предусматриваются следующие величины ПН = 25, 40, 60 %.
Режим S7 – это такой продолжительный режим, когда на нагрев оказывают влияние время пуска и реверса.
![]()
Режим S8 – это такой продолжительный режим постоянно меняющейся нагрузки.
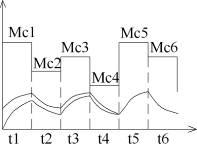
τнач=τа
τконеч=τр
При выполнении нескольких циклов устанавливается устойчивый тепловой цикл, когда перегрев в начале цикла и перегрев в конце цикла равны.
18. Выбор рода тока и напряжения. Выбор типа привода. Выбор конструкции.
Выбор двигателя.
Выбор двигателя осуществляется в несколько этапов:
1. выбор рода тока и напряжения. 2. выбор типа электропривода 3. выбор двигателя по конструкции.
4. выбор мощности двигателя: а) предварительный выбор мощности двигателя б) уточненный выбор мощности двигателя.
Выбор типа привода. Выбор рода тока и напряжения.
Тип привода выбирается в зависимости от источника тока. Существуют два типа источника: 1. источник переменного тока; 2. источник постоянного тока.
Пусть имеется сеть переменного тока.
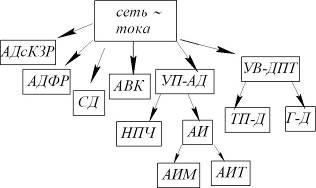
где АДсКЗР – асинхронный двигатель с коротко замкнутым ротором; АДФР – асинхронный двигатель с фазным ротором;
СД – синхронный двигатель; АВК – система асинхронного вентильного каскада; УП-АД – управляемый преобразователь - асинхронный двигатель; УВ-ДПТ – управляемый выпрямитель – двигатель постоянного тока; Г-Д – генератор-двигатель ТП-Д – тиристорный преобразователь-двигатель.
АИ – автономный инвертор. АИН – автономный инвертор напряжения. АИТ – автономный инвертор тока.
Если по условиям технологического процесса не требуется регулирования скорости в этом случае применяется АДсКЗР.
Если по условиям пускового момента и пускового тока АДсКЗР не подходит, то используют АДФР.
Если по условиям технологического процесса допустимо высокое напряжение и не требуется регулировки скорости, то используется СД.
Если условия более требовательны, то используют АВК.
Если предъявляются высокие требования к плавности и диапазону регулирования используют системы УВ-ДПТ и УП-АД.В свою очередь система УП-АД разделяется на НПЧ и АИ. АИ подразделяется на АИТ и АИН.
Рассматривают все возможные варианты и выбирают наиболее экономичный из конкурентоспособных.
Пусть имеется источник постоянного ток.

Где ДНВ – двигатель независимого возбуждения; ДПВ – двигатель последовательного возбуждения; ДСВ – двигатель смешанного возбуждения; ИТ-Д – система источник тока – двигатель.
Если по условиям технологического процесса возможен режим х.х., используется ДНВ
Если необходимо приводить в действие транспортеры, эскалаторы, троллейбусы, и т.д. в которых практически отсутствует режим х.х. то применяется ДПВ или ДСВ.
В специальных приводах используется система ИТ-Д, т.е. такая система которая обеспечит постоянство регулирования тока.
Выбор двигателя по конструкции.
Двигатель по конструкции может выбираться из следующих соображений:
1) В соответствии с географическими или климатическими условиями. По географическим и климатическим условиям изготавливают двигателя серий: ХЛ – для холодного климата, У – умеренного климата, УХЛ – умеренно-холодный климат, Т – тропический климат, М – морской.
2). По условиям работы, особенно для работы в шахтах изготавливают двигатели взрыво и, пожаро защищенные.
3). По расположению на возвышенных участках, необходимо помнить, что при повышении на 100 м. мощность теряется на 1%, т.о. если необходимо расположить двигатель на высоте 3000 м. необходимо иметь 30% против расчетного.
4). По конструктивным особенностям: двигателя горизонтального и вертикального исполнения, с одним или двумя выходного выходными контактами.
19. Предварительный выбор мощности и уточненный выбор мощности и соответствующие режимы Si (S1 , S2 , …S8 ).
Выбор мощности двигателя.
Выбор мощности двигателя осуществляется в 2 этапа.
1. предварительный выбор мощности; Для металлорежущих станков, для объектов цветной металлургии и т.д. двигатель выбирают по некоторым заданным эмпирическим формулам, либо по нагрузочной диаграмме механизма
2. уточненный выбор мощности. Если двигатель работает с перегрузкой, то он начинает сильно греться, изоляция выходит из строя. Если двигатель работает с недогрузкой, то он работает с более низким КПД, с более низким cosφ и занимает больше площадей, из-за этого выходит из строя.
20. Метод последовательной коррекции.
Синтез системы по методом ЛЧХ состоит из следующих действий:
1) Построение ЛАХ неизменяемой части системы L0(), так называемой располагаемой ЛАХ.
2) Построение желаемой ЛАХ системы на основании требований к ее динамическим показателям.
Определение передаточной функции корректирующего устройства.
При последовательной коррекции желаемая ЛАХ определяется выражением

Отсюда следует

ЛАХ последовательного корректирующего устройства определяется вычитанием располагаемой ЛАХ из желаемой.
Определив ЛАХ корректирующего устройства, можно по ней найти его передаточную функцию и вычислить ее параметры. По этим данным, используя приведенные в литературе таблицы, определяются принципиальная схема корректирующего устройства и рассчитываются численные значения элементов схемы.
При построении желаемой ЛАХ ее делят на три участка: низкочастотный, среднечастотный и высоко частотный. Среднечастотный участок определяется асимптотой, пересекающей ось частот, протяженностью влево и вправо до первых сопрягающих частот. Слева от него располагается низкочастотный участок, справа – высокочастотный.
Низкочастотная часть желаемой ЛАХ выбирается из условий требуемой точности. Если синтезируемая система должна быть статической, то для получения заданной точности, как это следует из (5.1), коэффициент передачи должен удовлетворять условию
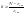 (5.3)
(5.3)
Если в системе предполагается иметь астатизм 1- го порядка, то коэффициент передачи выбирается из условия требуемой точности по скорости задающего воздействия
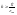 (5.4)
(5.4)
Этот вывод следует непосредственно из (5.2).
Достаточно точно низкочастотная часть строиться по требуемой точности воспроизведения гармонического воздействия

Передаточная функция системы по ошибке в частотной области может быть записана следующим образом
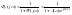
Для того, чтобы ошибка воспроизведения была минимальной, необходимо чтобы А(k)>>1. Тогда амплитуда ошибки определяется выражением
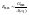
Для обеспечения требуемой точности на АЧХ налагается требование
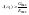 (5.5)
(5.5)
С точки зрения ЛЧХ это означает, что низкочастотный участок желаемой ЛАХ должен проходить не ниже некоторой контрольной точки, построенной по выражению
 (5.6)
(5.6)
Часто
при проектировании следящих систем
задаются максимальная скорость слежения
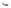 и максимальное ускорение слежения
и максимальное ускорение слежения
 .
По этим данным можно подобрать
эквивалентное гармоническое воздействие
с параметрами
.
По этим данным можно подобрать
эквивалентное гармоническое воздействие
с параметрами


Отсюда
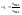
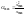 (5.7)
(5.7)
По этим координатам строиться контрольная точка. Доказано [2], что для обеспечения заданной точности в этом случае требуется, чтобы низкочастотная часть желаемой ЛАХ не заходила в запретную зону, ограниченную асимптотами с наклонами -20дб/дек и –40деб/дек, которые сопрягаются в контрольной точке.
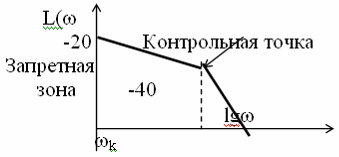
Рис. 5.4. Запретная зона
Наклон и протяженность среднечастотного участка определяются необходимыми запасами устойчивости. С этой точки зрения желательно, чтобы ось частот пересекал участок ЛАХ с наклоном -20дб/дек протяженность не менее одной декады. Хорошие результаты получаются, если частота среза и ближайшая частота сопряжения 1 справа от нее находятся в соотношении 1/c2. При выполнении этих требований обычно получают 20 и /c tp 2/c .
Не всегда удается выполнить построение такого среднечастотного участка. В этих случаях следует руководствоваться какими – либо соображениями, вытекающими из конкретной задачи или рекомендациями, приведенными в литературе.
Высокочастотный участок желаемой ЛАХ находиться ниже оси частот и не оказывает существенного влияния на процесс регулирования. Поэтому, по возможности, его нужно выбирать так, чтобы он совпадал с соответствующим участком располагаемой ЛАХ. Такой выбор существенно упрощает схему корректирующего устройства. Исключение составляет случай, когда высокочастотный участок располагаемой ЛАХ соответствует колебательному звену с малым показателем затухания. В этом случае высокочастотный участок желаемой ЛАХ должен проходить так, чтобы его удаление от оси частот на резонансной частоте удовлетворяло условию
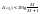 (5.8)
(5.8)
где М- показатель колебательности системы, который выбирается в пределах от 1.1 до 1.3.
21. Постановка задачи оптимального управления и критерии оптимальности.
Постановка задачи.
Необходимо найти алгоритм управления электромеханической системой описываемой дифференциальными уравнениями:



переводящий ее из начального состояния х0 в конечное состояние хк при минимизации критерия оптимальности и выполнении ограничений, накладываемых на систему:
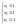
Кроме того, могут быть дополнительные ограничения на производную по току якорной цепи и момент упругого взаимодействия масс.
Критерии оптимальности могут быть различны: максимум быстродействия, производительности; минимум нагрева, расхода энергии или топлива; максимум надежности; наилучшее качество и др. Всему комплексу этих требований, или комплексному критерию оптимальности, не может отвечать ни одна система, так как, во-первых, критерии взаимно исключают друг друга, во-вторых, если даже удастся вычислить ритм управления по этому комплексному критерию, то его технически невозможно будет реализовать.
Наиболее часто пользуются критериями оптимальности в виде минимизации функционалов:

Критерий максимального быстродействия.
Если
функция
 =1,
то критерий оптимальности в виде
минимизации функционала
=1,
то критерий оптимальности в виде
минимизации функционала
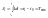
является критерием максимального быстродействия. Он означает, что система переводится из начального положения х0 в конечное положение хк за минимально возможное время.
На базе этого критерия построены многие системы: оптимальные по быстродействию приводы прокатных станов, металлорежущих станков, механизмов передвижения. Данная теория широко освещается в литературе и результаты ее могут быть применены к другим критериям.
Недостаток этого критерия: система, оптимальная по быстродействию, будет давать отличные результаты только при управляющем воздействии.
Критерий качества переходного процесса
Обозначим за х отклонение выходной координаты от установившегося значения. Алгоритм управления должен быть построен таким образом, чтобы площадь под кривой х2 была минимальной. Для уменьшения колебательности необходимо минимизировать квадратичные отклонения от производной выходной координаты.
Критерий
качества переходного процесса
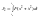
Физический смысл: алгоритм управления должен быть таким, чтобы запрещались не только квадратичные отклонения выходной величины, но и ее производной. В результате переходный процесс будет наименее возможно колебательным. При минимизации этого критерия работают системы подчиненного регулирования.
Недостатком критерия является ограниченность его применения только при управляющем воздействии (пуско-тормозные режимы и режим реверса).
Критерий аналитического конструирования регулятора.
В
общем виде критерий оптимальности
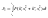
Физический смысл: алгоритм управления должен быть построен таким образом, чтобы обеспечивался минимум квадратичных отклонений всех координат при минимальном расходе энергии управления.
Этот критерий наиболее подходит для решения космических задач, где необходимо свести к минимуму отклонение всех координат: притяжение земли, лоитяжение со стороны других планет и т.д. - при минимальном расходе топлива.
Для электромеханических систем этот критерий не совсем подходит, так как при управляющем воздействии (пуск, реверс, торможение) необходимо, чтобы минимальным было квадратичное отклонение скорости, причем требование одновременно минимального отклонения тока не только ке нужно, но и вредно.
Следовательно, по управляющему воздействию необходим такой алгоритм управления, который минимизировал бы функционал
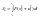
При возмущающем воздействии необходим такой алгоритм управления, который минимизировал бы функционал
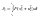
При возмущающем воздействии необходимо, чтобы алгоритм управления был таким, при котором квадратичные отклонения усилия были минимальны, причем практически безразлично, как будет вести себя скорость. Это особенно важно, например, для электромеханических систем, где режимы стопорения являются рабочими. Желательно использовать устройство, которое осуществляет, переключение с алгоритма, построенного по критерию J4, на алгоритм, построенный по критерию J5.
Ценность критерия аналитического регулирования регуляторов заключается в том, что алгоритм управления получается в виде линейной функции от координат системы. Алгоритм управления определяется на основании математических методов оптимального управления. Система управления называется оптимальной в смысле выбранного критерия оптимальности, например, оптимальная по быстродействию система.
22. Комбинированные оптимальные системы управления.
СПР обладают рядом преимуществ: 1. Простата синтезу СУ. 2. Простата наладки СУ.
Кроме достоинств СПР обладает следующими недостатками: 1. С увеличением числа контуров быстродействие уменьшается. 2. СПР дают отличные результаты только при управляющем воздействии.
Системы оптимального управления по сравнению с СПР имеют следующие недостатки: 1. Более сложный синтез. 2. Более сложная практическая реализация.
Достоинством оптимальной системы является то что можно найти коэффициент оптимальных обратных связей по всем координатам или по выбранному количеству координат и их производных.
Если использовать положительные свойства систем подчиенного регулирования и положительные свойства оптимальных систем управления, особенно в части реализации оптимальных обратных связей, то получим качественно новую систему – комбинированную оптимальную систему управления.
Комбинированная оптимальная система управления (КОСУ) отличается от комбинированной классической системы тем, что в комбинированной системе используются управления по отклонению и по возмущению, а в КОСУ используется 2 типа систем управления.
Т.о. КОСУ называется система построенная по принципу последовательной коррекции внутренних координат (ток возбуждения, тоя якоря, скорость двигателя) и оптимальному управлению внешних координат (упругого момента и скорости 2-ой массы).
23. Метод динамического программирования.
Характеристика метода динамического программирования
Метод динамического программирования (метод Гамильтона-Якоби-Беллмана) ориентирован на поиск оптимального управления широкого класса систем. Метод ДП точен для дискретных систем и приближенный для непрерывных систем.
ДП применяется для оптимизации динамических и статических систем, для детерминированных и стохастических систем.
Принцип ДП: оптимальное управление не зависит от предыстории процесса изменения состояния системы, а определяется лишь ее состоянием в рассматриваемый момент времени.
Этот принцип определяет требования, предъявляемые к последующему движению системы, начиная с текущего момента времени и до конца процесса управления. Из принципа ДП следует, что поиск оптимального управления по этому методу, как правило, идет от конца процесса к его началу.
Постановка задачи оптимального управления и ее решение методом ДП для дискретных систем
Имеем дискретную систему, описываемую системой из m разностных уравнений первого порядка вида
![]() ,
(7.1)
,
(7.1)
где
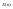 - вектор переменных состояния системы
размерностью 1 ´
m,
- вектор переменных состояния системы
размерностью 1 ´
m,
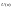 -
вектор управления разностью 1 ´
r.
-
вектор управления разностью 1 ´
r.
 - известные функции, n - номер цикла.
- известные функции, n - номер цикла.
Заданы
также интервал управления n=0 ¸
N, начальное состояние системы
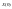 и ограничения на управление
и ограничения на управление
 .
.
Необходимо
найти оптимальное управление
 на отрезке n = 0 ¸
N, чтобы обеспечить условия минимума
функционала (целевой функции) вида:
на отрезке n = 0 ¸
N, чтобы обеспечить условия минимума
функционала (целевой функции) вида:
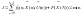 ,
(7.2)
,
(7.2)
где
 - подынтегральная функция, F – терминальная
функция.
- подынтегральная функция, F – терминальная
функция.
Для решения задачи методом ДП для каждого цикла n составляется уравнение Беллмана:
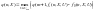 (7.3)
(7.3)
с краевым условием вида:
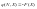 (7.4)
(7.4)
Величина
 есть приращение функционала J на цикле
n. Затем для каждого цикла решаются
уравнения (7.3) и определяются
есть приращение функционала J на цикле
n. Затем для каждого цикла решаются
уравнения (7.3) и определяются
 .
Далее находят оптимальный вектор
управления на n – ом цикле, такой, чтобы
выполнялось условие:
.
Далее находят оптимальный вектор
управления на n – ом цикле, такой, чтобы
выполнялось условие:
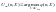 (7.5)
(7.5)
при n = 0 ¸ N – 1.
При
этом векторы оптимального управления
 и оптимального состояния системы
и оптимального состояния системы
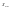 должны удовлетворять уравнениям
системы (7.1) и начальным условиям, то
есть:
должны удовлетворять уравнениям
системы (7.1) и начальным условиям, то
есть:
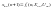 ,
n = 0 ¸
N – 1, i =
,
n = 0 ¸
N – 1, i =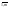
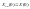 (7.6)
(7.6)
Решение задачи ищется прямым счетом, обычно с конца процесса, вектор оптимального управления определяется по формуле:
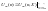 (7.7)
(7.7)
24. Принцип максимума Понтрягина.
Эффективным средством исследования задач оптимального управления является принцип максимума Понтрягина, представляющий собой необходимое условие оптимальности в таких задачах.
Теорема (принцип максимума Понтрягина).
Пусть
функции
 ,
,
 ,
..,
,
.., и, Ф, g1,
..., gm имеют частные производные по
переменным х1,
..., Хn
и непрерывны вместе с этими производными
по совокупности аргументов х
и, Ф, g1,
..., gm имеют частные производные по
переменным х1,
..., Хn
и непрерывны вместе с этими производными
по совокупности аргументов х ,
и
,
и
 U,
t
U,
t [to. Т]. Предположим, что (и, х)-решение
задачи (2.1). Тогда существует решение ψ
сопряженной системы (2.3), соответствующей
управлению и траектории х, и константа
[to. Т]. Предположим, что (и, х)-решение
задачи (2.1). Тогда существует решение ψ
сопряженной системы (2.3), соответствующей
управлению и траектории х, и константа  такие, что
такие, что
|  | + || ψ (t) || при t
| + || ψ (t) || при t [to, Т], и выполняются следующие условия:
[to, Т], и выполняются следующие условия:
а)
(условие максимума) при каждом t [to. Т] функция Гамильтона Н(х,u,t,ψ0,ψ),
достигает максимума по ν
[to. Т] функция Гамильтона Н(х,u,t,ψ0,ψ),
достигает максимума по ν U
при v=u (t), т. е.
U
при v=u (t), т. е.
H(x(t), u(t), t,ψ0,ψ ) =max H(x(t), v(t), t,ψ0,ψ ) (2.4)
б)(условие
трансверсальности на левом конце
траектории) существуют числа
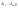 ,
такие, что
,
такие, что
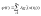 (2.5)
(2.5)
в)
(условие трансверсальности на правом
конце траектории) существуют числа  такие, что
такие, что
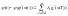 (2.6)
(2.6)
Центральным в теореме является условие максимума -(2.4).
Если отказаться от предположения о том, что конечный момент времени Т фиксирован, то теорема останется справедливой за исключением условия трансверсальности на правом конце траектории. Условие (2.6) заменим условием
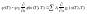
и добавить еще одно условие трансверсальности на правом конце траектории: