Идеальный диэлектрик состоит только из связанных между собой заряженных частиц. Свободных зарядов в нем нет, поэтому электро­проводность в идеальном диэлектрике отсутствует.

В реальных диэлектриках из-за наличия в них дефектов строения и ионогенной примеси име­ются свободные заряженные частицы (свободные заряды), кото­рые не связаны с определенными молекулами или атомами. Под действием приложенного электрического поля они направленно перемещаются (дрейфуют) в диэлектрике на относительно большие расстояния. Подходя к электродам, свободные заряды разряжаются на них, обу­словливая электрический ток. Поскольку содержание свободных за­рядов в диэлектриках ничтожно мало, их электропроводность очень низкая (в 10¹¹ – 10²⁶ раз меньше, чем у проводников).

Диэлектрические материалы используют в электротехнике в ос­новном для создания электрической изоляции, которая окружает токоведущие части электрических устройств и отде­ляет друг от друга элементы схемы или конструкции, находящиеся под различ­ными электрическими потенциалами.

Применение диэлектриков в конденсаторах позволяет получать требуемые значения емкости, а в некоторых случаях обеспечивает определенный характер зависимости этой емкости от внешних факторов. Диэлектрик конденсатора может запасать, а потом отдавать в цепь электрическую энергию (емкостный накопи­тель). Иногда конденсатор используют для разделения цепей постоянного и пе­ременного токов, для изменения угла фазового сдвига и т. д.

Некоторые диэлектрики применяют как для создания электрической изоля­ции, так и в качестве конденсаторных материалов (например, слюда, керамика, стекло, полистирольные и другие пленки). Тем не менее, требования к электро­изоляционным и конденсаторным материалам существенно различаются. Если от электроизоляционного материала требуется невысокая относительная диэлектри­ческая проницаемость и большое удельное сопротивление, то диэлектрик кон­денсатора, наоборот, должен иметь повышенную  и малое значение tg.

Диэлектрические материалы являются основными видами электротехниче­ских материалов, с которыми придется встретиться на практике будущим инженерам-электрикам.

Физические условия, в которых должна находиться и функционировать изоляция, накладывают определенные требования на физико-химические параметры материала, ограничивая возможные вид и тип используемых электротехнических материалов. Кроме того, при конст­руировании даже простейших изделий, предназначенных для работы в электри­ческом поле, необходимо четко представлять, какие процессы происходят в мате­риале, как влияет тот, или иной материал на работу других частей устройства, в том числе за счет перераспределения электрического поля. Здесь необходимо учитывать разноплановые характеристики материала:

---

– механические: плотность и вес материала, прочность;

– теплофизические: теплопроводность, теплоемкость, нагревостойкость, те­плостойкость и горючесть;

– электрофизические: диэлектрическая проницаемость, электропровод­ность, электрическая прочность, трекингостойкость;

– физико-химические: химическая стойкость, влагопро­ни­цаемость и т.д.

Чтобы оценить значи­мость каждого из них и понять, какие требования, в каждом конкретном случае, являются главными, а какие – второстепенными необхо­димо ясное понимание всего комплекса процессов, происходящих при функцио­нировании устройств.

Основными электрическими характеристиками диэлектриков являются диэлектрическая проницаемость , удельное объ­емное сопротивление , удельное поверхностное сопротивление _s, тан­генс угла диэлектрических потерь tg и электрическая прочность Е_пр.

Лабораторная работа № 1

ИЗМЕРЕНИЕ ДИЭЛЕКТРИЧЕСКОЙ ПРОНИЦАЕМОСТИ И УГЛА ДИЭЛЕКТРИЧЕСКИХ ПОТЕРЬ ТВЁРДЫХ
ДИЭЛЕКТРИКОВ

1.1. Цель работы

Изучить процессы поляризации в диэлектриках. Определить диэлектрическую проницаемость и тангенс угла диэлектрических потерь в образцах диэлектрических материалов.

1.2. Задачи работы

1. Измерить тангенс угла диэлектрических потерь и относительную диэлектрическую проницаемость.

2. Определить целесообразность применения диэлектрика в качестве изоляционного материала или в конденсаторе.

1.3. Краткие теоретические сведения

В отсутствие внешнего электрического поля все связанные и сво­бодные заряженные частицы диэлектрика, а также его полярные молекулы (диполи) расположены таким образом, что общий электри­ческий дипольный момент всех микроскопических объемов, занимае­мых этими частицами и диполями, равен или близок нулю. Под дейст­вием приложенного электрического поля все заряженные частицы смещаются из своих равновесных положений на ограниченные рас­стояния. Положительные заряды смещаются в направлении вектора внешнего поля, а отрицательные – в обратном направлении, образуя диполи (индуцированные диполи). Имеющиеся диполи ориентируют­ся по полю. Возникает поляризация диэлектрика, и его результирую­щий дипольный момент всех микрообъемов становится отличным от нуля. В таком состоянии диэлектрик называют поляризованным. Способ­ность диэлектриков поляризоваться под действием приложенного элек­трического поля является их фундаментальным свойством.

Диэлектрическая проницаемость  количественно характеризует спо­собность диэлектрика поляризоваться, а также оценивает степень его по­лярности; е является константой диэлектрического материала при опреде­ленной температуре и частоте электрического напряжения и показывает, во сколько раз заряд конденсатора с данным диэлектриком больше заряда конденсатора тех же размеров с вакуумом.

---

Заряд Q₀ на каждой пластине плоского конденсатора с вакуумом равен (по модулю):

,

соответственно ёмкость

, (1. 1)

где ₀ – диэлектрическая постоянная, или диэлектрическая проницаемость вакуума, ₀ = 8,85 10^–12 Ф/м, S – площадь каждой из пластин, d – зазор между пла­стинами, U – напряжение между ними.

Заряд Q_x на каждой пластине плоского конденсатора с диэлектриком равен (по модулю):

.

соответственно ёмкость

.

Диэлектрическая проницаемость  равна

, (1.2)

где Q_д –заряд, обусловленный поляризацией диэлектрика.

Диэлектрическими потерями называют мощность, рассеиваемую в диэлектрике при воздействии на него электрического поля и вы­зывающую нагрев диэлектрика.

Потери в диэлектриках наблюдаются как при переменном напряжении, так и при постоянном, поскольку в материале обнаруживается сквозной ток при по­стоянном напряжении, когда нет периодической поляризации. Качество материа­ла характеризуется значениями удельных объемного и поверхностного сопротив­лений. При переменном напряжении необходимо использовать другую характе­ристику качества материала, так как в этом случае, кроме сквозного тока, возни­кают дополнительные причины, вызывающие потери в диэлектрике.

Диэлектрические потери в электроизоляционном материале можно характеризовать рассеиваемой мощностью, отнесенной к единице объема, или удельными потерями; чаще для оценки способности диэлектрика рассеивать мощность в электрическом поле пользуются углом диэлектрических потерь, а также тангенсом этого угла.

Углом диэлектрических потерь называется угол, дополняющий до 90° угол фазового сдвига  между током и напряжением в емкост­ной цепи. Для идеального диэлектрика вектор тока в такой цепи будет опережать вектор напряжения на 90°, при этом угол диэлек­трических потерь  будет равен нулю. Чем больше рассеиваемая в диэлектрике мощность, переходящая в теплоту, тем меньше угол фазового сдвига  и тем больше угол  и его функция tg .

Недопустимо большие диэлектрические потери в электроизоляционном ма­териале вызывают сильный нагрев изготовленного из него изделия и могут при­вести к его тепловому разрушению. Даже если напряжение, приложенное к ди­электрику, недостаточно велико для того, чтобы за счет диэлектрических потерь мог произойти недопустимый перегрев, то и в этом случае большие диэлектриче­ские потери могут принести существенный вред, увеличивая, например, активное сопротивление колебательного контура, в котором использован данный диэлек­трик, а, следовательно, и величину затухания.

Природа диэлектрических потерь в электроизоляционных Природа диэлектрических потерь в электроизоляционных мате-риалах раз­лична в зависимости от агрегатного состояния вещества. Диэлектрические потери могут обусловливаться сквозным током или, как указывалось при рассмотрении явления поляризации, активными составляющими токов смещения.

---

В технических электроизоляционных материалах, помимо потерь от сквоз­ной электропроводности и потерь от замедленной поля-ризации, возникают диэлектрические потери, которые сильно влияют на электрические свойства диэлектриков. Эти потери вызываются на-личием изолированных друг от друга по­сторонних проводящих или полупроводящих включений углерода, оксидов железа; они значи-тельны даже при малом содержании таких примесей в электроизо­ляционном материале.

Дальнейшее рассмотрение диэлектрических материалов будем проводить на примере конденсатора.

В любом реальном конденсаторе при работе его на переменном токе неиз­бежны потери в диэлектрике, обусловленные переменной поляризацией. Кроме того, конденсатор имеет ещё активную проводимость через изоляцию электро­дов, поэтому реальный кон-денсатор представляется эквивалентной схемой в виде идеальной ёмкости, последовательно или параллельно соединённой с актив­ным сопротивлением (рис. 1.1 а, б).

Векторные диаграммы и схемы замещения для идеального диэлектрика и диэлектрика с потерями показаны на рис. 1.1.

Из векторной диаграммы тангенс этого угла равен отношению активного и реактивного токов или отношения активной мощности P_A к реактивной P_C.

.

Иногда для характеристики устройства с диэлектриком опре-деляют доб­ротность – параметр обратный тангенсу угла ди-электрических потерь:

.

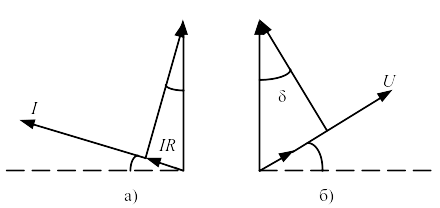
Рис. 1.1 – Последовательная (а) и параллельная (б) схемы замещения реального конденсатора и соответствующие векторные диаграммы

Для последовательной схемы

,

для параллельной

.

Сопоставление формул для последовательной и параллельной схем заме­щения показывает, что они дают взаимно противоположные зависимости пара­метров цепи конденсатора от частоты. Это объясняется тем, что ни одна из схем замещения не отражает полностью тех реальных процессов, которые имеют ме­сто в конденсаторах.

Последовательная схема и соответствующие ей формулы лучше отражают физические свойства реального конденсатора в области высоких частот (более 1 МГц), параллельная схема даёт более правильные результаты в области низких частот. В области средних частот обе схемы являются достаточно удовлетвори­тельными.

Методы и средства измерений емкости, угла диэлектрических потерь и диэлектрической проницаемости

1. По определению угол диэлектрических потерь – угол, дополняющий 90° угол фазового сдвига между током и напряжением в емкостной цепи (рис. 1.2). Угол сдвига определяется как отношение времени сдвига к периоду колеба­ний, и для перевода в радианы помножить на 2π.

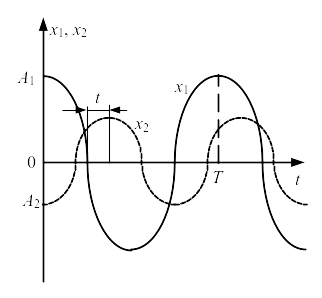
Рис. 1.2 Осциллограмма тока и напряжения в цепи с емкостной нагрузкой

,

.

2. Наиболее часто значения С и tg  на частоте 50 Гц опреде-ляют при помо­щи мостов переменного тока. Предел измерения моста по емкости должен быть не менее емкости образца, а по tg  превышать примерно в 2 раза tg  образца. Принципиальная схема такого моста показана на рис. 1.3, а.

---

Схема, приведённая на рис. 1.3,а позволяет получить большую точ­ность измерений. Испытуемый образец подключают к мосту параллельно с гра­дуированным измерительным конденсатором С₀. Производят уравновешивание моста и записывают С’₀ и С’₁. Затем отключают образец и вновь уравновешивают мост изменением С₀ и С и записывают значения С”₀ и С”₁. Значения С_х и tg . на­ходят по формулам:

,

.

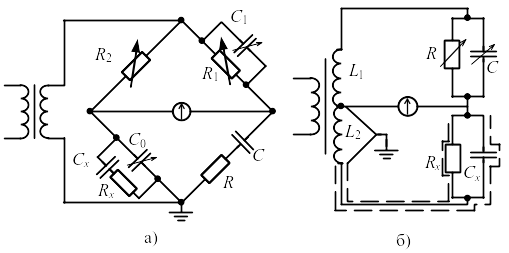
Рис. 1.3. Основные схемы мостов для измерения С и tg: а – метод замещения; б – схема трансформаторного моста.

Высокую точность измерений позволяют получить трансфо-рматорные мосты переменного тока (рис. 1.3,б), в которых уравно-вешивание выполняется изменением емкости и индуктивности. Изменением отношения L₁/L₂ уста­навливают диапазон изменения, а точное уравновешивание осуществляется ре­гулировкой С и R. Уравне-ния равновесия моста:

,

.

3. Для измерений на частоте 50 Гц применяют как прямые, так и косвенные измерения. Измерение емкости осуществляется при помо-щи приборов непосред­ственной оценки или приборов сравнения (мостов).

Измерения при помощи стрелочных приборов непосредственной оценки не применяются из-за невысокой точности и сложности расчетов, однако те же ме­тоды измерения с использованием цифровых приборов и ЭВМ позволяют полу­чить удовлетворительные результаты.

Схема с использованием амперметра, вольтметра и ваттметра показана на рис. 1.4, а. Ваттметр должен обладать высокой чувствительностью, посколь­ку значения мощности потерь незначительны. Искомые значения величин вы­числяют по формулам:

,

,

.

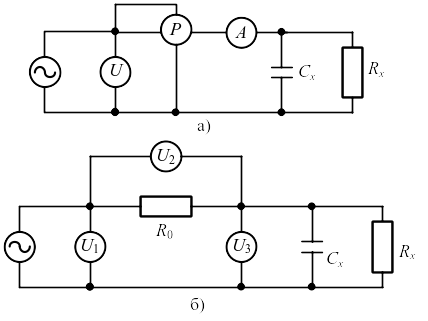
Рис. 1.4. Косвенные методы измерения

На рис. 1.4, б приведена схема, использующая три вольтметра. Значе­ния C_x и tg  находят по формулам:

, (1.3)

, (1.4)

, (1.5)

. (1.6)

Обе схемы чувствительны к изменению частоты.

4. Рассматривая переходные процессы в цепи (рис. 1.5), состоящей из последовательно соединенных участков с датчиком тока R, источником тока I и конденсатором емкостью С, протекающий через конденсатор ток будет равен изменению заряда в единицу времени:

Так как

,

то

,

откуда

. (1.7)

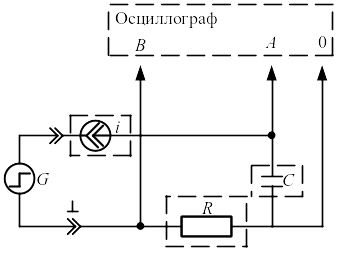
Рис. 1.5. Схема электрическая соединений установки для измерения емкости конденсатора

На схему (рис. 1.5) подаётся переменное напряжение прямоугольной формы и рассматривается заряд конденсатора при постоянном токе.

Частота сигнала выбирается таким образом, чтобы осциллограмма тока (канал В) имела участок t, на котором значение тока I установилось и поддер­живалось источником тока i на одном уровне.

Измерение приращения напряжения U(U_c) производится по осцилло­грамме канала A в интервале вышеописанного прямолинейно-го участка t.

Подставляя полученные значения U , t и значение источника тока I в формулу (1.7) получим ёмкость конденсатора С.

5. Диэлектрическая проницаемость материала образца может быть найде­на как отношение ёмкости С_х при заданной конфигурации электродов и испытуе­мом материале в качестве диэлектрика к ёмкости С₀, тех же электродов без образ­ца (но с сохранением геометрических размеров) в вакууме (параметры, необхо­димые для расчёта приведены на корпусе минимодуля).

---

Смотрите также файлы

• Макро 2 семестр.docx

• Компьютерный английский Met_196.doc

• Информатика.docx

• Задачи по физике.docx

• дневник ПГС.doc