ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 23.10.2023
Просмотров: 84
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Контрольная работа №2
Задача 1. Тема: «Нормальное распределение».
Предположим, что в течение года цены на акции некоторой компании подчинялись нормальному закону распределения с Математическим ожиданием, равным 48 у.е., и стандартным отклонением (СКО), равным 6. Чему равна вероятность того, что в случайно выбранный день обсуждаемого периода цена на акцию: будет более 60 у.е.;
Решение
Для нормального закона распределения случайной величины вероятность попадания в заданный интервал равна: где Ф(????) – функция Лапласа, ???? − математическое ожидание; ???? − среднее квадратическое отклонение.
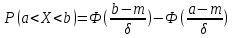
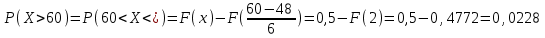
Ответ: 0,0228
Задача 2. Тема: «Интервальные оценки».
Для изучения различных демографических характеристик населения выборочно обследовалось 300 семей города. Оказалось, что среди обследованных семей 15% состоят из двух человек. В каких пределах находится в генеральной совокупности доля семей, состоящих из двух человек, если принять доверительную вероятность равной 0.95?
Решение.
В данной задаче требуется построить доверительный интервал для генеральной доли. Определим выборочную долю р.
Из 300 семей 15% состоит из 2-х человек
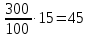семей состоит из 2-х человек.Значит, выборочная доля таких семей составляет
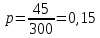
Поскольку объем выборки n=300>30,
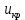найдем из таблиц Лапласа с учетом доверительной вероятности 
: 
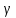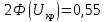
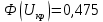
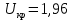
Предельная ошибка выборки
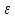равна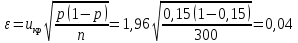
Таким образом, доверительный интервал для генеральной доли по выборочным данным равна
(0,15-0,04;0,15+0,04) или (0,11; 0,19)
Доля семей, состоящая из 2-х человек, с вероятностью 0,95 находится в пределах от 11% до 19%.
Задача 3. Тема: «Проверка статистических гипотез»
Поступление страховых полисов в 130 филиалах страховых компаний в регионе А составило
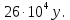е., в регионе В на 100 филиалов пришлось 
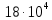у.е. Дисперсия величины страховых взносов в регионе А равна
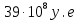, в регионе В —
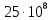(у.е.) . На уровне значимости α = 0.01 определите, существенно ли различается средняя величина поступления страховых взносов в регионах А и В из расчета на один филиал.Решение
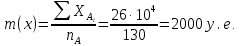
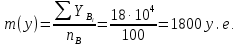
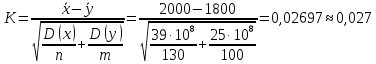
Ф(
=
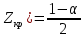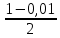= 0,995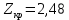
Полученное значение меньше критического, значит, средняя величина поступления страховых взносов в регионах А и В из расчета на один филиал отличается несущественно.
Задача 4. Тема: «Критерий согласия Пирсона».
С помощью критерия согласия Пирсона на уровне значимости α = 0,05 выяснить, можно ли считать случайную величину X, заданную в виде сгруппированного статистического ряда, нормально распределенной с параметрами x и s, рассчитанными по выборке.
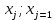 | [2.3;2.5] | [2.5;2.7] | [2.7;2.9] | [2.9;3.1] | [3.1;3.3] | [3.3;3.5] |
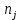 | 3 | 6 | 9 | 8 | 5 | 2 |
Для каждого из интервалов определим середину. Имеем
| группы | середина интервала | nj | xj*nj | x-x ̅ | (x-x ̅)^2) | ((x-x ̅)^2)*nj |
| 2.3-2.5 | 2,4 | 3 | 7,2 | -0,47 | 0,22 | 0,67 |
| 2.5-2.7 | 2,6 | 6 | 15,6 | -0,27 | 0,07 | 0,45 |
| 2.7-2.9 | 2,8 | 9 | 25,2 | -0,07 | 0,01 | 0,05 |
| 2.9-3.1 | 3 | 8 | 24 | 0,13 | 0,02 | 0,13 |
| 3.1-3.3 | 3,2 | 5 | 16 | 0,33 | 0,11 | 0,54 |
| 3.3-3.5 | 3,4 | 2 | 6,8 | 0,53 | 0,28 | 0,56 |
| итого | | | 94,8 | 0,16 | 0,70 | 2,39 |
=
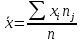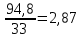
Вычислим дисперсию
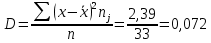
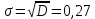
Нулевую гипотезу сформулируем как утверждение, что случайная величина Х имеет нормальное распределение с указанными выше параметрами
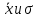.Вычислим теоретические частоты, учитывая n=33,
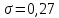, h=0,2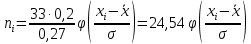
| группы | Ui | φ(ui) | ni |
| 2.3-2.5 | -1,76 | 0,0863 | 2,12 |
| 2.5-2.7 | -1,01 | 0,242 | 5,94 |
| 2.7-2.9 | -0,27 | 0,3857 | 9,47 |
| 2.9-3.1 | 0,47 | 0,3565 | 8,75 |
| 3.1-3.3 | 1,22 | 0,1872 | 4,59 |
| 3.3-3.5 | 1,96 | 0,0573 | 1,41 |
| итого | 0,61 | 1,315 | 32,27 |
Сравним эмпирические и теоретические частоты. Составим расчетную таблицу, из которой найдем наблюдаемое значение критерия.
 |  |  |  |  |
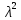
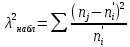
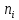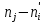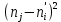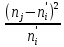| 3 | 2.1 | 0.9 | 0.81 | 0.39 |
| 6 | 5.9 | 0.1 | 0.01 | 0.002 |
| 9 | 9.5 | 0.5 | 0.25 | 0.03 |
| 8 | 8.7 | 0.7 | 0.49 | 0.06 |
| 5 | 4.6 | 0.4 | 0.16 | 0.03 |
| 2 | 1.4 | 0.6 | 0.36 | 0.26 |
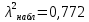
По таблице критических точек распределения
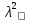по уровню значимости 
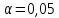и числу степеней свободы к=6-1-2=3 находим критическую точку правосторонней критической области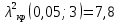
Так как
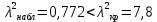то гипотеза о нормальном распределении генеральной совокупности не отклоняется. Случайная величина Х имеет нормальное распределение с указанными параметрами.Задача 5. Тема: «Ранговая корреляция».
По заданной таблице рангов найти выборочный коэффициент ранговой корреляции Спирмена и проверить значимость полученного результата при α = 0.05.
На конкурсе красоты 12 участниц проранжированы по двум признакам: X — артистизм, Y — красота.
| Ранг 1 | 11 | 4 | 10 | 1 | 8 | 9 | 2 | 12 | 6 | 7 | 5 |
| Ранг2 | 11 | 1 | 12 | 6 | 2 | 10 | 5 | 9 | 7 | 8 | 3 |
Коэффициент ранговой корреляции Спирмена.
Присвоим ранги признаку Y и фактору X.
| X | Y | ранг X, dx | ранг Y, dy |
| 3 | 4 | 3 | 4 |
| 11 | 11 | 11 | 11 |
| 4 | 1 | 4 | 1 |
| 10 | 12 | 10 | 12 |
| 1 | 6 | 1 | 6 |
| 8 | 2 | 8 | 2 |
| 9 | 10 | 9 | 10 |
| 2 | 5 | 2 | 5 |
| 12 | 9 | 12 | 9 |
| 6 | 7 | 6 | 7 |
| 7 | 8 | 7 | 8 |
| 5 | 3 | 5 | 3 |
Матрица рангов.
| ранг X, dx | ранг Y, dy | (dx - dy)2 |
| 3 | 4 | 1 |
| 11 | 11 | 0 |
| 4 | 1 | 9 |
| 10 | 12 | 4 |
| 1 | 6 | 25 |
| 8 | 2 | 36 |
| 9 | 10 | 1 |
| 2 | 5 | 9 |
| 12 | 9 | 9 |
| 6 | 7 | 1 |
| 7 | 8 | 1 |
| 5 | 3 | 4 |
| 78 | 78 | 100 |
Проверка правильности составления матрицы на основе исчисления контрольной суммы:
Сумма по столбцам матрицы равны между собой и контрольной суммы, значит, матрица составлена правильно.
По формуле вычислим коэффициент ранговой корреляции Спирмена.
Связь между признаком Y и фактором X умеренная и прямая.
Оценка коэффициента ранговой корреляции Спирмена.
Значимость коэффициента ранговой корреляции Спирмена
Для того чтобы при уровне значимости α проверить нулевую гипотезу о равенстве нулю генерального коэффициента ранговой корреляции Спирмена при конкурирующей гипотезе H