ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 23.10.2023
Просмотров: 85
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
i. p ≠ 0, надо вычислить критическую точку:
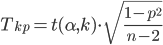
где n - объем выборки; p - выборочный коэффициент ранговой корреляции Спирмена: t(α, к) - критическая точка двусторонней критической области, которую находят по таблице критических точек распределения Стьюдента, по уровню значимости α и числу степеней свободы k = n-2.
Если |p| < Тkp - нет оснований отвергнуть нулевую гипотезу. Ранговая корреляционная связь между качественными признаками не значима. Если |p| > Tkp - нулевую гипотезу отвергают. Между качественными признаками существует значимая ранговая корреляционная связь.
По таблице Стьюдента находим t(α/2, k) = (0.05/2;10) = 2.634
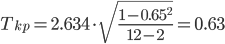
Поскольку Tkp < p, то отклоняем гипотезу о равенстве 0 коэффициента ранговой корреляции Спирмена. Другими словами, коэффициент ранговой корреляции статистически - значим и ранговая корреляционная связь между оценками по двум тестам значимая.
Задача 6. Тема: «Линейная корреляция и регрессия».
Для приведенных исходных данных постройте диаграмму рассеяния и определите по ней характер зависимости. Рассчитайте выборочный коэффициент корреляции Пирсона, проверьте его значимость при α = 0.05. Запишите уравнение регрессии и дайте интерпретацию полученных результатов.
Компанию по прокату автомобилей интересует зависимость между пробегом автомобиля (X) и стоимостью ежемесячного технического обслуживания (Y). Для выяснения характера этой зависимости было отобрано 15 автомобилей.
РЕШЕНИЕ:
Построим график исходных данных
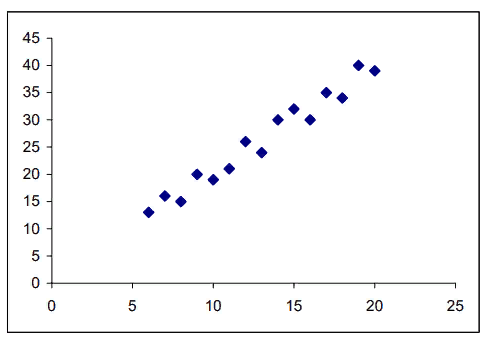
По графику видно, что зависимость прямая, линейная.
Выборочный коэффициент линейной корреляции Пирсона найдем по формуле:
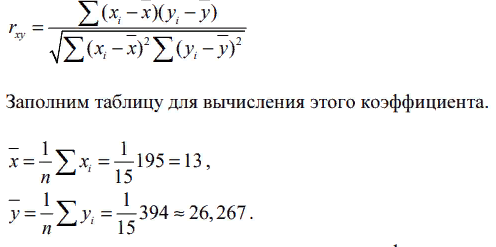
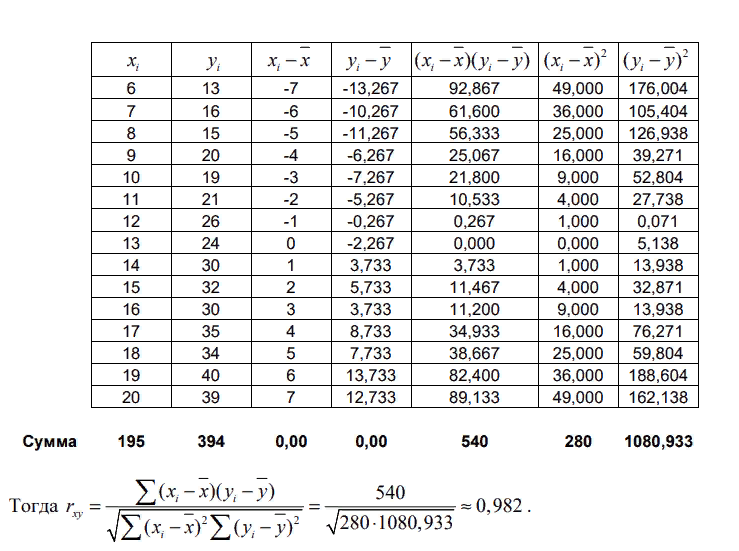
Введем нулевую гипотезу H0 :r =0 . Проверим эту гипотезу об отсутствии корреляционной зависимости (о незначимости коэффициента корреляции). Вычислим значение критерия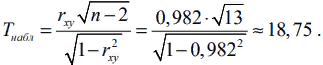
Найдем критическую точку по уровню значимости α = 0,05 и числу степеней свободы k =n − 2 =13, получаем tкр. = 2,16. Так как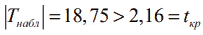
, , следует отвергнуть нулевую гипотезу H0 :r 0 = , то есть корреляционная зависимость есть (существенна), коэффициент корреляции статистически значим.
Уравнение регрессии Y на X имеет вид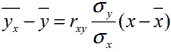
. Найдем средние квадратические отклонения.
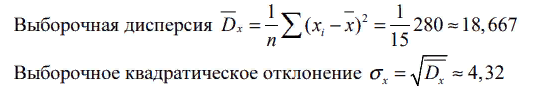
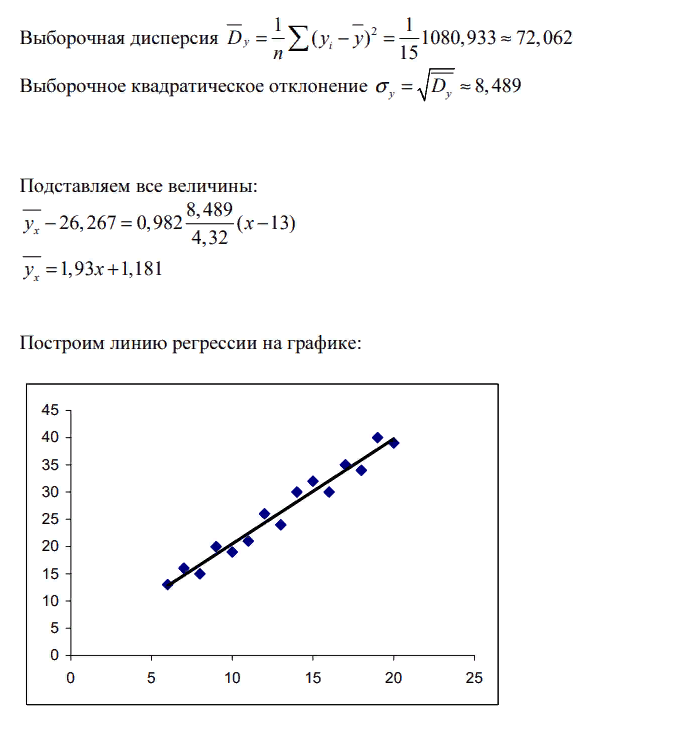
Таким образом, наблюдается очень тесная прямая связь между величиной пробега автомобиля и стоимостью ежемесячного технического обслуживания, которая выражается уравнением регрессии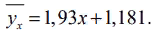
. Через каждый год пробега стоимость обслуживания возрастает в среднем на 1,93.
где n - объем выборки; p - выборочный коэффициент ранговой корреляции Спирмена: t(α, к) - критическая точка двусторонней критической области, которую находят по таблице критических точек распределения Стьюдента, по уровню значимости α и числу степеней свободы k = n-2.
Если |p| < Тkp - нет оснований отвергнуть нулевую гипотезу. Ранговая корреляционная связь между качественными признаками не значима. Если |p| > Tkp - нулевую гипотезу отвергают. Между качественными признаками существует значимая ранговая корреляционная связь.
По таблице Стьюдента находим t(α/2, k) = (0.05/2;10) = 2.634
Поскольку Tkp < p, то отклоняем гипотезу о равенстве 0 коэффициента ранговой корреляции Спирмена. Другими словами, коэффициент ранговой корреляции статистически - значим и ранговая корреляционная связь между оценками по двум тестам значимая.
Задача 6. Тема: «Линейная корреляция и регрессия».
Для приведенных исходных данных постройте диаграмму рассеяния и определите по ней характер зависимости. Рассчитайте выборочный коэффициент корреляции Пирсона, проверьте его значимость при α = 0.05. Запишите уравнение регрессии и дайте интерпретацию полученных результатов.
Компанию по прокату автомобилей интересует зависимость между пробегом автомобиля (X) и стоимостью ежемесячного технического обслуживания (Y). Для выяснения характера этой зависимости было отобрано 15 автомобилей.
| X | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| Y | 3 | 16 | 15 | 20 | 19 | 21 | 26 | 24 | 30 | 32 | 30 | 35 | 34 | 40 | 39 |
РЕШЕНИЕ:
Построим график исходных данных
По графику видно, что зависимость прямая, линейная.
Выборочный коэффициент линейной корреляции Пирсона найдем по формуле:
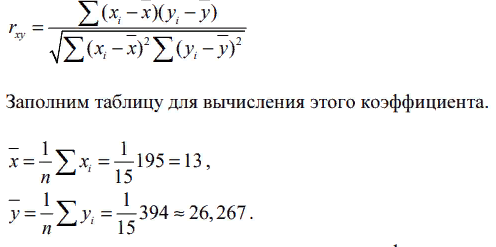
Введем нулевую гипотезу H0 :r =0 . Проверим эту гипотезу об отсутствии корреляционной зависимости (о незначимости коэффициента корреляции). Вычислим значение критерия
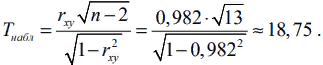
Найдем критическую точку по уровню значимости α = 0,05 и числу степеней свободы k =n − 2 =13, получаем tкр. = 2,16. Так как
, , следует отвергнуть нулевую гипотезу H0 :r 0 = , то есть корреляционная зависимость есть (существенна), коэффициент корреляции статистически значим.Уравнение регрессии Y на X имеет вид
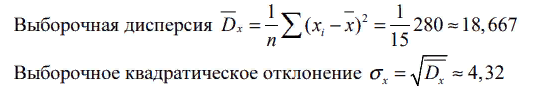
. Найдем средние квадратические отклонения. Таким образом, наблюдается очень тесная прямая связь между величиной пробега автомобиля и стоимостью ежемесячного технического обслуживания, которая выражается уравнением регрессии
. Через каждый год пробега стоимость обслуживания возрастает в среднем на 1,93.