Добавлен: 24.10.2023
Просмотров: 43
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Задача №1 (Вариант 12)
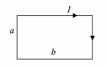
Найти индукцию магнитного поля в центре прямоугольного проводящего контура со сторонами a и b, по которому течет ток силой I.
Дано:
I=5 А,
a=12 см=0,12 м
b=6 см=0,06 м
Найти:
B=?
Решение:
Для решения задачи необходимо использовать:
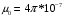 Гн/м − магнитная постоянная.
Гн/м − магнитная постоянная.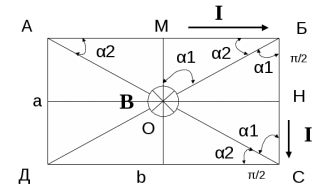
Рассмотрим четыре участка, АБ, БС, СД, ДА.
Направление вектора магнитной индукции на каждом участке определим по правилу буравчика. В точке О результирующий вектор магнитной индукции направлен от нас. Применим принцип суперпозиции.
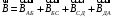 (1)
(1)или в проекции на ось вектора
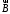
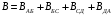 (2)
(2)Определим модуль вектора магнитной индукции на участке АБ.
Индукция магнитного поля в произвольной точке О, созданного отрезком проводника с током конечной длины, определим используя закон Био - Савара - Лапласа.
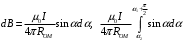 , (3)
, (3)Где: Rом - расстояние от точки О до проводника АБ; –α2 и α1+π/2 углы, образованные радиус-вектором, проведенном в т. О соответственно из начала и конца проводника, с направлением тока.
Определим модуль вектора магнитной индукции на каждом участке.
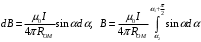 , (4)
, (4)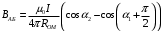 , (5)
, (5)Определим модуль вектора магнитной индукции на участке БС.
Индукция магнитного поля в произвольной точке О, созданного отрезком проводника с током конечной длины, определим используя закон Био - Савара - Лапласа.
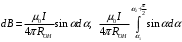 , (6)
, (6)Где: Rон - расстояние от точки О до проводника БС; – α1 и α2+π/2 углы, образованные радиус-вектором, проведенном в т. О соответственно из начала и конца проводника, с направлением тока.
Определим модуль вектора магнитной индукции на каждом участке.
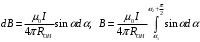
, (7)
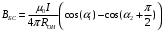 , (8)
, (8)Теперь для упрощения расчетов синусов и косинусов углов найдем гипотенузы прямоугольных треугольников
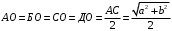
и расстояния
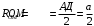 ,
, 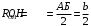
Тогда формулы (5) и (8) упростим следующим образом
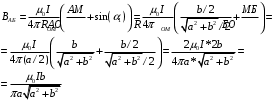 (9)
(9)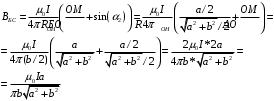 (10)
(10)Далее учитывая равенство отрезков прямоугольника
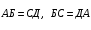 преобразуем формулу (2)
преобразуем формулу (2)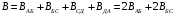 (11)
(11)Подставляя формулы (9) и (10) в формулу (11) получим итоговое выражения для вычисления индукцию магнитного поля в точке О
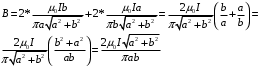 (12)
(12)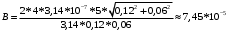
Ответ:
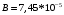 Тл.
Тл.Задача №2 (Вариант 12)
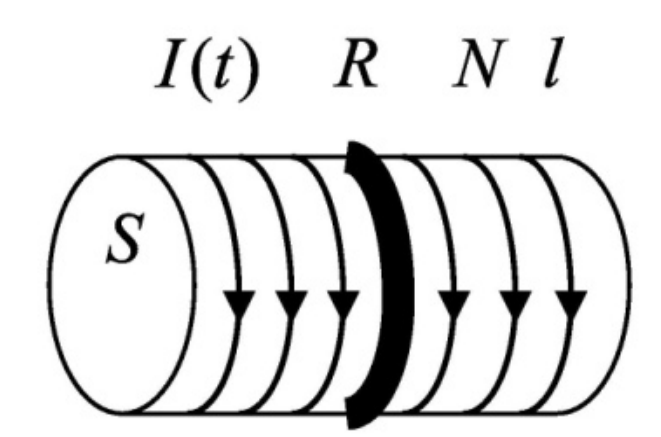
На соленоид длиной l=10 см и площадью поперечного сечения S=5 кв. см надет проволочный виток сопротивлением R = 1 Ом. Обмотка соленоида имеет N=500 витков, и по нему идет ток, сила которого меняется со временем по заданному закону
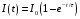 . Найти зависимость от времени силы тока
. Найти зависимость от времени силы тока 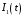 в проволочном витке и построить график этой зависимости в времени от 0до t.
в проволочном витке и построить график этой зависимости в времени от 0до t.Дано:
l=10 см=0,1 м
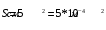
R=1 Ом
N=500
N1=1
I0=2 А
τ=1 с
t=1 с
Найти:
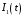 =?
=?Решение:
Для решения задачи необходимо использовать:
 Гн/м − магнитная постоянная и т.к. в задаче не оговаривается среда в которой все происходит, то примем, что μ=1 – магнитная проницаемость для воздушной среды.
Гн/м − магнитная постоянная и т.к. в задаче не оговаривается среда в которой все происходит, то примем, что μ=1 – магнитная проницаемость для воздушной среды.
ЭДС индукции в соленоиде находим по формуле
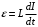 , (1)
, (1)Где
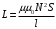 - индуктивность соленоида с N витками, длиной l и площадью S.
- индуктивность соленоида с N витками, длиной l и площадью S.ЭДС индукции, наводимая в проволочном витке, при изменении тока в соленоиде равна
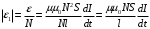 (2)
(2)Тогда ток, проходящий через виток по закону Ома равен
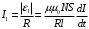 (3)
(3)Исходя из известных значений I0 и τ найдем закон изменения тока в соленоиде в зависимости от времени
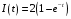 (4)
(4)Теперь продифференцируем полученное выражение
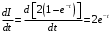 (5)
(5)Подставляя формулу (5) в формулу (3) получим итоговую формулу
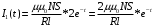 (6)
(6)Подставляя все известные значения, в итоге получим
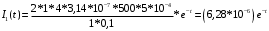 А
Аили
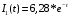 мкА
мкАПостоим график данной функции в интервале
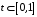 сек.
сек.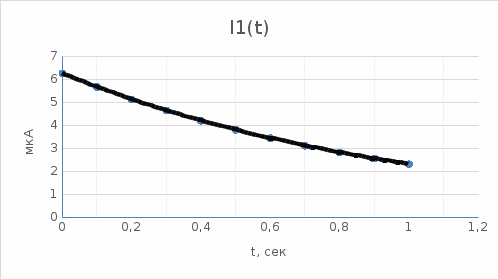
Ответ:
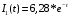 мкА.
мкА.Задача №3 (Вариант 12)
П
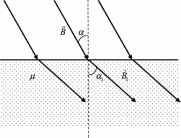 олупространство, заполненное веществом с магнитной проницаемостью μ, отделено от вакуума бесконечной плоскостью. В вакууме имеется однородное магнитное поле с индукцией В, направление которого составляет угол α с нормалью к поверхности раздела. Найти модуль индукции B1 магнитного поля в веществе и угол α1 между вектором индукции магнитного поля в веществе и нормалью к поверхности раздела.
олупространство, заполненное веществом с магнитной проницаемостью μ, отделено от вакуума бесконечной плоскостью. В вакууме имеется однородное магнитное поле с индукцией В, направление которого составляет угол α с нормалью к поверхности раздела. Найти модуль индукции B1 магнитного поля в веществе и угол α1 между вектором индукции магнитного поля в веществе и нормалью к поверхности раздела.Дано:
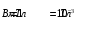
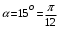
μ=15
Найти:
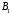
=?
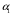 =?
=?Решение:
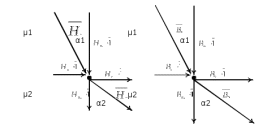
Т.к. в точке на границе 2-х сред нету тока, то касательные составляющие вектора напряженности магнитного поля (следствие первого уравнения Максвелла) в веществе 1 и веществе 2 равны
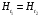 , (1)
, (1)Т.к.
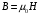 , где
, где  Гн/м − магнитная постоянная то формулу (1) запишем как
Гн/м − магнитная постоянная то формулу (1) запишем как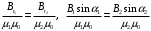 (2)
(2)Т.к. необходимо найти 2 неизвестных воспользуемся еще законом преломления магнитных полей на границе 2-х сред
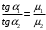 (3)
(3)Теперь преобразуем формулы (2) и (3) для наших исходных данных, т.е.
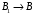 ,
, 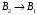 ,
, 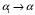 ,
, 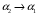 ,
, 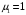 ,
, 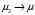
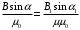 (4)
(4)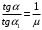 (5)
(5)В начале из формулы (5) найдем угол α1
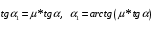 (6)
(6)Получаем
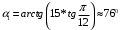
Теперь из формулы (4) выразим

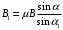
В итоге найдем
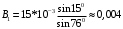 Тл
ТлОтвет:
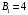 мТл,
мТл, 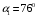 .
.