23. Движение спутников Земли. Космические скорости. Законы Кеплера.

Движение спутника Земли начинается с

7,91 км/с, при меньших ускорениях его остановит атмосфера, и он возвратится обратно.

Используются четыре значения космических скоростей. Первая космическая скорость — 7,9 км/с — скорость для выхода на орбиту вокруг Земли.

Вторая космическая скорость — 11,1 км/с — скорость для ухода из сферы притяжения Земли и выхода в межпланетное пространство.

Третья космическая скорость — 16,67 км/с — скорость для ухода из сферы притяжения Солнца и выхода в межзвездное пространство.

Законы Кеплера:

Первый закон. Орбита планеты представляет собой эллипс, в одном из фокусов которого находится Солнце.

Второй закон. За равные промежутки времени линия, соединяющая планету с Солнцем, описывает равные площади.

Третий закон. Периоды обращения соотносятся с размерами эллипсов так, что квадрат периода пропорционален кубу полуоси орбиты.

Расстояние от Земли	Сила	Ускорение	Скорость
h=0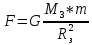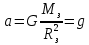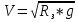
h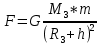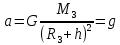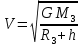

24. Силы инерции в поступательно движущихся системах координат.

Силы инерции при поступательном движении нерациональной системы.

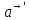- ускорение тела относительно НИС;

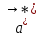- ускорение НИС относительно инерциальной.

Тогда ускорение тела относительно ИС:

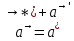
25. Силы инерции во вращающихся системах координат.

Сила инерции, действующая на тело, находящееся во вращающейся системе называется центробежной. Направлена она по горизонтальной к оси вращения.

---

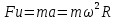
26. Виды колебаний. Уравнение гармонических колебаний. Скорость и ускорение гармонических колебаний.

Виды колебаний: 1) Свободные, 2) Гармонические, 3) Вынужденные, 4) Затухающие

ГК – это колебания, происходящие по закону синуса или косинуса.

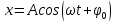xm – амплитуда колебаний, ????0 = начальная фаза колебаний, ???? – циклическая частота = 2????????, ???? = ????t+????0 – фаза колебаний в данный момент времени.

(

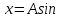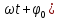
27. Динамика гармонических колебаний. Дифференциальное уравнение гармонических колебаний.

Первая (скорость) и вторая (ускорение) производные по времени от гармонически колеблющейся величины s также совершают гармонические колебания с той же циклической частотой:


28. Энергия гармонических колебаний.

Сжимая или растягивая пружину, отклоняя маятник, мы совершаем работу против тех или иных сил. Эта работа должна превращаться в потенциальную энергию колеблющегося тела.

Кинетическая энергия тела, совершающего гармонические колебания:



Потенциальная энергия тела, совершающего гармонические колебания:



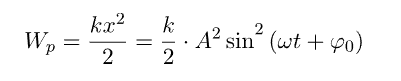
29. Математический и физический маятники.

Математическим маятником называется материальная точка, подвешенная на нерастяжимой невесомой нити, совершающая колебательное движение в одной вертикальной плоскости под действием силы тяжести.

Физическим маятником называется твердое тело, закрепленное на неподвижной горизонтальной ocи (оси подвеса), не проходящей через центр тяжести, и совершающее колебания относительно этой оси под действием силы тяжести.

30. Затухающие колебания. Логарифмический декремент затухания.

Затухающие колебания колебания, при которых амплитуда колебаний уменьшается с течением времени, что обусловлено потерей энергии колебательной системы.

Логарифмический декремент затухания - натуральный логарифм отношения амплитуд двух соседних перерегулирований.

---

31. Вынужденные колебания. Резонанс.

Вынужденные колебания – это колебания, происходящие под действием внешней периодически действующей силы.

Резонанс – это явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к собственной частоте колебательной системы.
32. Сложение одинаково направленных колебаний. Биения.

Для простоты рассмотрим сначала случай, когда частоты складываемых колебаний одинаковы.Общие решения складываемых гармонических колебаний имеют вид:



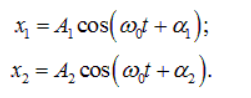
Где x₁, x₂ — переменные, описывающие колебания, A₁, A₂ — их амплитуды, , — начальные фазы. Результирующее колебание:



Биения — это периодическое изменение амплитуды колебаний, возникающее при сложении двух гармонических колебаний с близкими частотами.
33. Сложение взаимно перпендикулярных колебаний. Фигуры Лиссажу.

При сложении взаимно перпендикулярных колебаний с различными, но кратными частотами результирующее колебание происходит по траекториям, называемым фигурами Лиссажу;



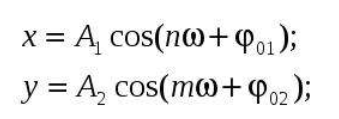
Вид фигуры Лиссажу зависит от соотношения частот, от амплитуд и начальных фаз складывается колебаний.

34. Образование волн. Поперечные и продольные волны. Скорость волны.

Если в каком-либо месте упругой среды (твердой, жидкой или газообразной) возбудить колебания ее частиц, то вследствие взаимодействия между частицами это колебание будет распространяться в среде от частицы к частице с некоторой скоростью. Процесс распространения колебаний в пространстве называется волной.

---

Продольная волна – это волна, в которой частицы среды колеблются вдоль направления распространения волны.

Поперечная волна - это волна, в которой частицы среды колеблются в направлениях, перпендикулярных к направлению распространения волны.

Скорость волны – это скорость, с которой перемещается в среде волновой фронт:

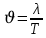
35. Уравнение плоской волны. Волновое уравнение.

1) уравнение плоской волны:



Волновое уравнение − линейное дифференциальное уравнение в частных производных, описывающее малые колебания струны, колебательные процессы в сплошных средах и в электродинамике. В общем случае волна, распространяющаяся в пространстве, описывается уравнением


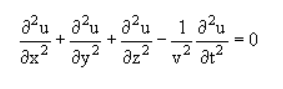
36. Стоячие волны.

Стоячая волна - это волна, которая образуется при наложении двух волн с одинаковой амплитудой и частотой, когда волны движутся навстречу друг другу. Практически стоячие волны возникают при отражении волн от преград. Падающая на преграду волна и бегущая ей навстречу отраженная волна налагаясь друг на друга, дают стоячую волну.

37. Эффект Доплера.

Эффект Доплера — физическое явление, связанное с уменьшением или увеличением частоты волны, принимаемой наблюдателем, в результате движения источника волны.
38. Постулаты Эйнштейна. Опыт Майкельсона. Перообразная Лоренца.

Альберт Эйнштейн, создавая свою теорию, в качестве основы брал экспериментальные данные. Он попытался их объяснить, выдвинув всего два постулата:

1)Равенство любых систем отсчёта, движущихся с постоянной и прямолинейной скоростью.

2)Неизменность скорости света в любой системе отсчёта.
Опыт Майкельсона — физический опыт, поставленный. Майкельсоном в 1881 году, с целью измерения зависимости скорости света от движения Земли относительно эфира.

Преобразованиями Лоренца в физике, в частности, в специальной теории относительности (СТО), называются преобразования, которым подвергаются пространственно-временные координаты (

---

x,y,z,t) каждого события при переходе от одной инерциальной системы отсчета (ИСО) к другой.
39. Относительность длин и промежутков времени. Относительность одновременности.

Результаты измерения длины стержня относительны и зависят от скорости его движения относительно системы отсчета; длина всегда получается меньше собственной длины (множитель меньше единицы), и чем больше скорость движения стержня относительно какой-либо системы отсчета, тем меньше его длина, измеренная в этой системе.

Относительность промежутков ремени состоит в том, что ход часов зависит от движения наблюдателя. Движущиеся часы отстают от неподвижных: если какое-либо явление имеет определенную длительность для движущегося наблюдателя, то оно кажется более продолжительным для неподвижного.

В физике относительность одновременности - это концепция, согласно которой отдаленная одновременность – независимо от того, происходят ли два пространственное разделенных события в одно и то же время – не является абсолютной, а зависит от системы отсчета наблюдателя.
40. Зависимость массы тела от скорости.

Масса тела, измеренная в той системе отсчета, относительно которой тело покоится называемой массой покоя m0. Тогда масса, измеренная наблюдателем, движущимся относительно тела со скоростью;



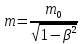
41. Размеры и масса молекул.

Размеры молекул очень малы.

Порядок величины диаметра молекулы 1*10^{-8 см = 1*10-10 м}. Порядок величины объёма молекулы 1*10^{-20 м3}

Массу можно определить, если абсолютное значение массы молекулы разделить на единичную атомную массу.
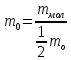
42. Идеальный газ. Параметры состояния. Законы идеального газа.
Идеальный газ - газ, для которого взаимодействием и размерами молекул можно пренебречь.

Параметры идеального газа характеризуется тремя параметрами:

---

Смотрите также файлы

• Тема Процессы и инструменты управления проектами системный подход Смоделируйте процесс Планирование персонала проекта.docx

• Практическая работа 1, курс РЕАЛИЗАЦИЯ ТРЕБОВАНИЙ ОБНОВЛЕННЫХ ФГОС НОО, ФГОС ООО В РАБОТЕ УЧИТЕЛЯ.docx

• Задачи Распространять педагогические знания среди родителей. 2.docx

• Решение Запас ресурса (Q, млрд т) вычисляется по формуле q запас ресурсов, млрд т q годовая добыча ресурсов, млрд тгод.docx

• Инструкция по сигнализации на железнодорожном транспорте рф.(Иси ржд приложение 7 к птэ актуальная версия c изменениями скачать).docx