ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 24.10.2023
Просмотров: 42
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
М
 ИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
ИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИфедеральное государственное бюджетное образовательное учреждение
высшего образования
«Тольяттинский государственный университет»
Институт химии и энергетики
(наименование института полностью)
Кафедра /департамент /центр1промышленная электроника
(наименование кафедры/департамента/центра полностью)
13.03.02.
(код и наименование направления подготовки, специальности)
Электроэнергетика электротехника. Электроснабжение
(направленность (профиль) / специализация)
Практическое задание № 4
по учебному курсу «Высшая математика 3
»
(наименование учебного курса)
| Студент | Исаев Данил Сергеевич | |
| | (И.О. Фамилия) | |
| Группа | ЭЭТбп-1901б | |
| | | |
| Преподаватель |
| |
| | (И.О. Фамилия) | |
Практическая работа 4
Вариант 8
Задача 1.
Построить область интегрирования, изменить порядок интегрирования в интеграле.
1)Дано:
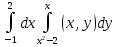
Построим область интегрирования, ограниченную кривыми:
y=
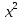 -2 –парабола с вершиной в точке O (0;-2)
-2 –парабола с вершиной в точке O (0;-2)y=x -прямая, которая проходит через начало координат
Изобразим область D в системе координат
График:
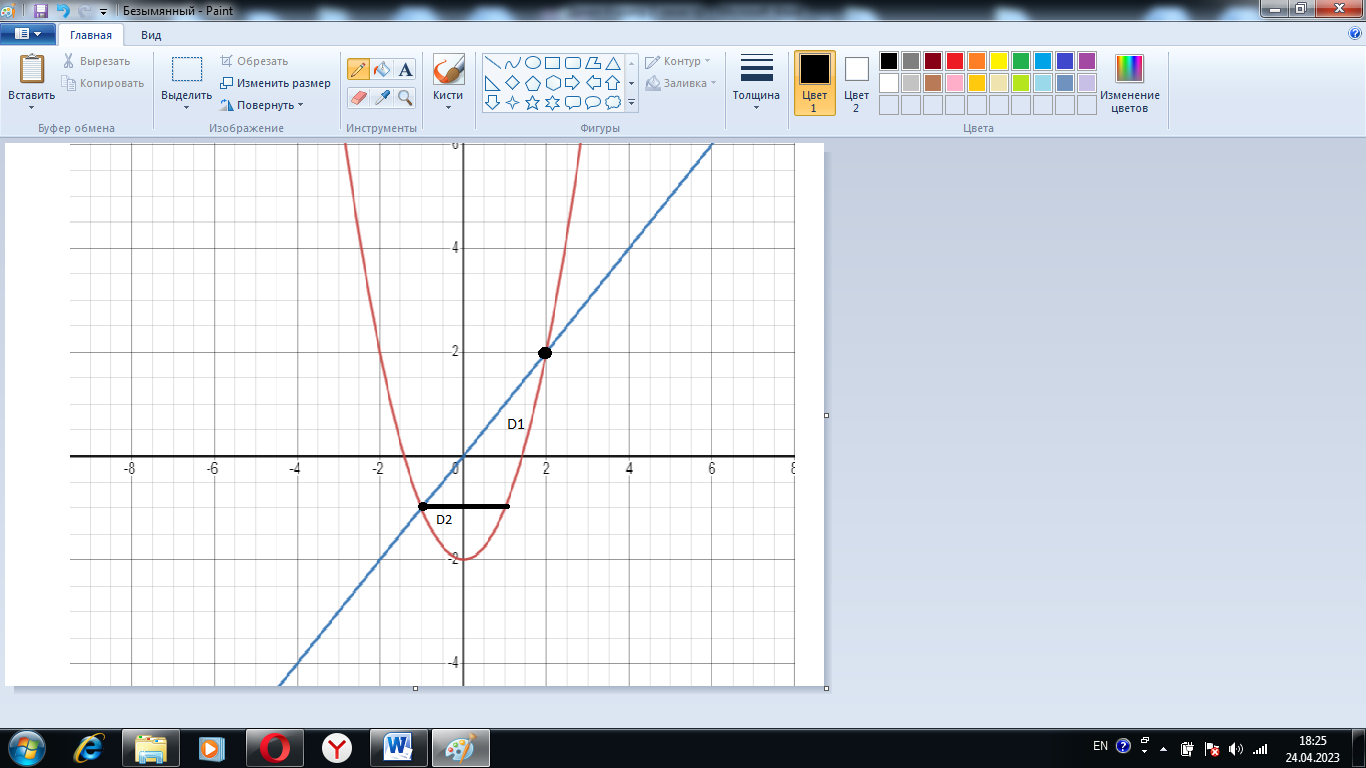
Найдем точки пересечения кривых:
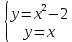
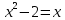
 -x- 2=0
-x- 2=0 D =1+4·1·2=9 ⇒
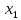 =2
=2 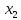 =-1
=-1Точки пересечения графиков: A (-1; -1) , B (2; 2)
Для изменения пределов перейдем от y(x) к x(y)
Для пределов:
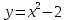 ⇒ x=
⇒ x=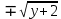
y=x ⇒ x=y
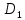 – предел: -1⋜y⋜ 2; y ⋜x⋜
– предел: -1⋜y⋜ 2; y ⋜x⋜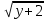
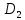 - предел: -2 ⋜y⋜-1 ; -
- предел: -2 ⋜y⋜-1 ; -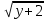 ⋜x⋜
⋜x⋜ 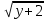 ⇒
⇒Область интегрирования равна сумме двух областей
D =
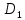 +
+ 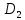
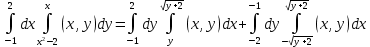
Задание 2
Вычислить двойные интегралы.
Дан двойной интеграл:
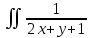 dxdy, если
dxdy, еслиy=x; y=3x; x=3
1)Для определения области D построим график
График:
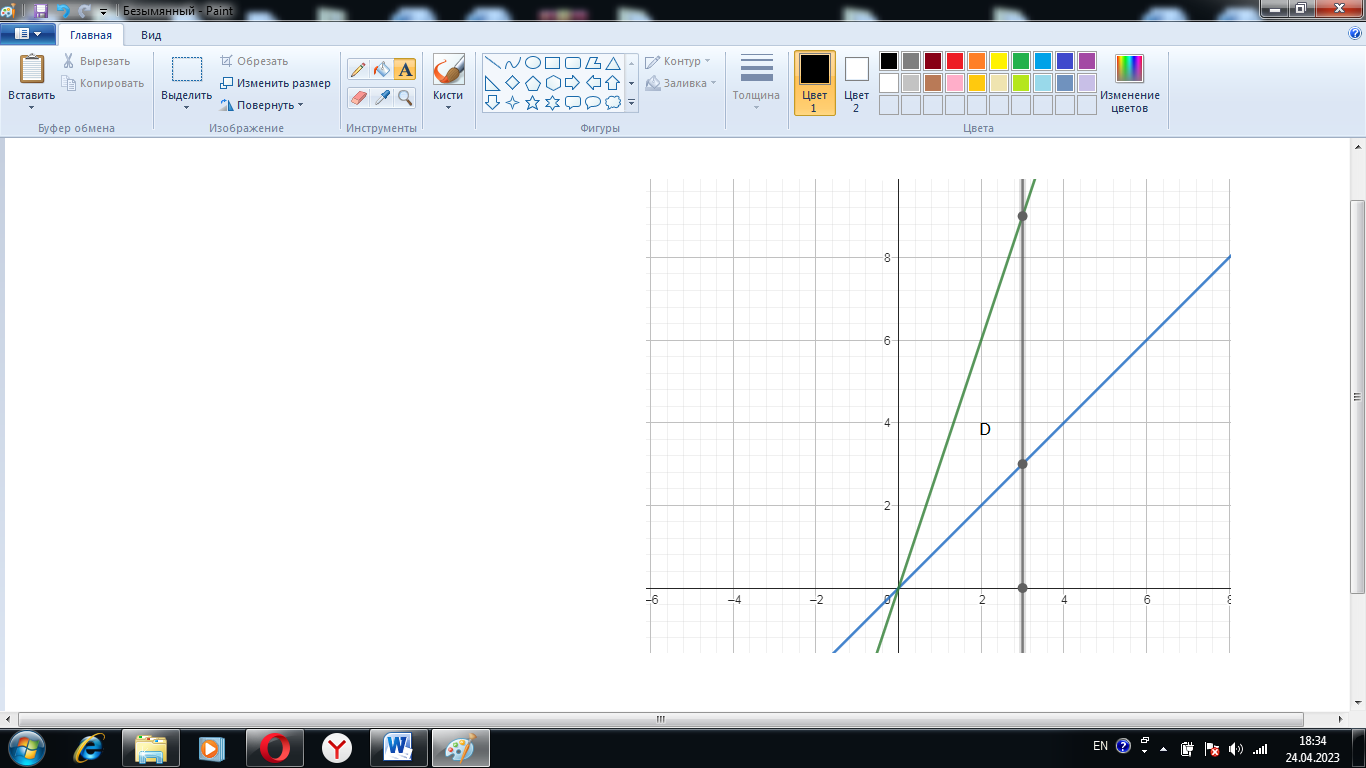
2) Спроецируем область D на ось ОХ и запишем систему неравенств
0 ⋜ x⋜ 3
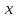 ⋜ y ⋜ 3x ⇒
⋜ y ⋜ 3x ⇒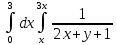 dy
dy3) Вычислим двукратный интеграл в два этапа.
Вычислим внутренний интеграл:
Решение:
Внесем значение под знак дифференциала
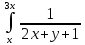 dy(
dy(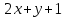 )
)Вычислим по формуле:
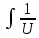
du=ln│U│
Получим интеграл:
 du =
du =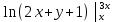
Функция непрерывна на интервале.
По формуле Ньютона-Лейбница
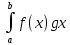 = F(x)
= F(x)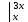 = F(b)-F(a)
= F(b)-F(a)F(x)
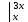 = F(3x)-F(x) =
= F(3x)-F(x) =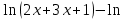 (
(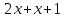 ) =
) = 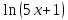 -
-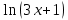 ⇒
⇒ du =
du =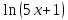 -
-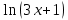
Вычислим внешний интеграл:

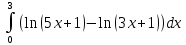
Интеграл разности равен разности интегралов
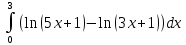 =
=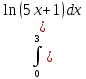 -
-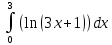
Найдем интеграл :
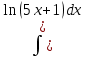
Сделаем подстановку
Пусть U=5x+1 ⇒ x=
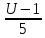 dx=
dx=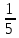 du
du
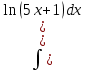
Проведем интегрирование по частям
fg′=fg -f′g, где
f = lnU f′ =
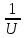
g′ =1 g =
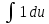 = U ⇒
= U ⇒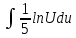 =
= 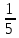
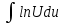 =
=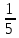 (u·lnu -
(u·lnu -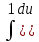
=
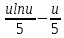 =
=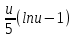 , где U=5x+1 ⇒
, где U=5x+1 ⇒  =
=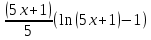 = (x+
= (x+ )
)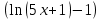 =
=x
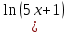 +
+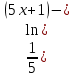 x -
x -
 = x
= x +
+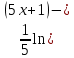 x -
x -
Найдем интеграл :
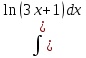
Сделаем подстановку
Пусть U=3x+1 ⇒ x=
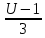 dx=
dx=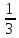 du
du
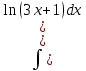
Проведем интегрирование по частям
fg′=fg -f′g, где
f = lnU f′ =

g′ =1 g =
 = U ⇒
= U ⇒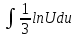 =
= 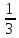
 =
=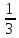 (u·lnu -
(u·lnu - =
=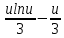 =
=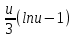 , где U=3x+1 ⇒
, где U=3x+1 ⇒ 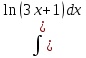 =
=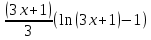 = (x+
= (x+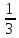 )
)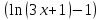 =
=x
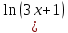 +
+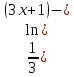
x -

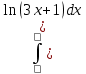 = x
= x +
+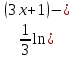 x -
x -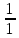
По формуле Ньютона-Лейбница
 = F(x)|₀³= F(b)-F(a) |₀³= F(3)-F(0)
= F(x)|₀³= F(b)-F(a) |₀³= F(3)-F(0) F(3) =( x
 +
+ x -
x - ) – (x
) – (x +
+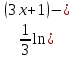 x -
x - = 3(ln(5·3+1))+
= 3(ln(5·3+1))+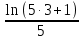 -3-
-3- -(3ln(3·3+1))+
-(3ln(3·3+1))+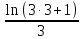 -3-
-3- =
=(3ln16 +
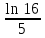 -3
-3 -3ln(9+1))-
-3ln(9+1))-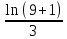 +3
+3 ) =
) =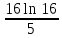 -3
-3
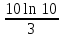 +3
+3
F(3) =
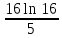 -3
-3
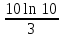 +3
+3
F(0) =( x
 +
+ x -
x - ) – (x
) – (x +
+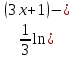 x -
x -